3.2. Графическое решение задачи Reddy Mikks

Решим графически задачу компании Reddy Mikks о производстве краски (2). Для удобства перенумеруем ограничения

Условия неотрицательности переменных и показывают, что пространство допустимых решений будет лежать в первом квадранте.

Каждому из ограничений (1) – (4) на плоскости соответствует полуплоскость. Пересечение этих полуплоскостей образует пространство допустимых решений — многоугольник (см. рис. 1).

Возьмем значение целевой функции равное 10 (значение выбрано произвольно) и построим соответствующую линию уровня целевой функции . Направление возрастания целевой функции можно определить с помощью вектора градиента. В данном случае градиент целевой функции равен вектору (для определения направления возрастания целевой функции можно также просто взять большее значение, например 15, и построить соответствующую ему линию уровня). Таким образом, при движении в направлении, задаваемым вектором целевая функция возрастает. Целевая функция будет возрастать до тех пор, пока прямые (линии уровня), соответствующие возрастающим значениям этой функции, пересекают пространство допустимых решений. Точка пересечения пространства допустимых решений и прямой, соответствующей максимально возможному значению целевой функции, и будет точкой оптимума.

В нашей задаче оптимальное решение соответствует точке , являющейся пересечением прямых, соответствующих ограничениям (1) и (2). Координаты этой точки и являются оптимальным решением задачи, при этом значение целевой функции равно (см. Рис. 1).

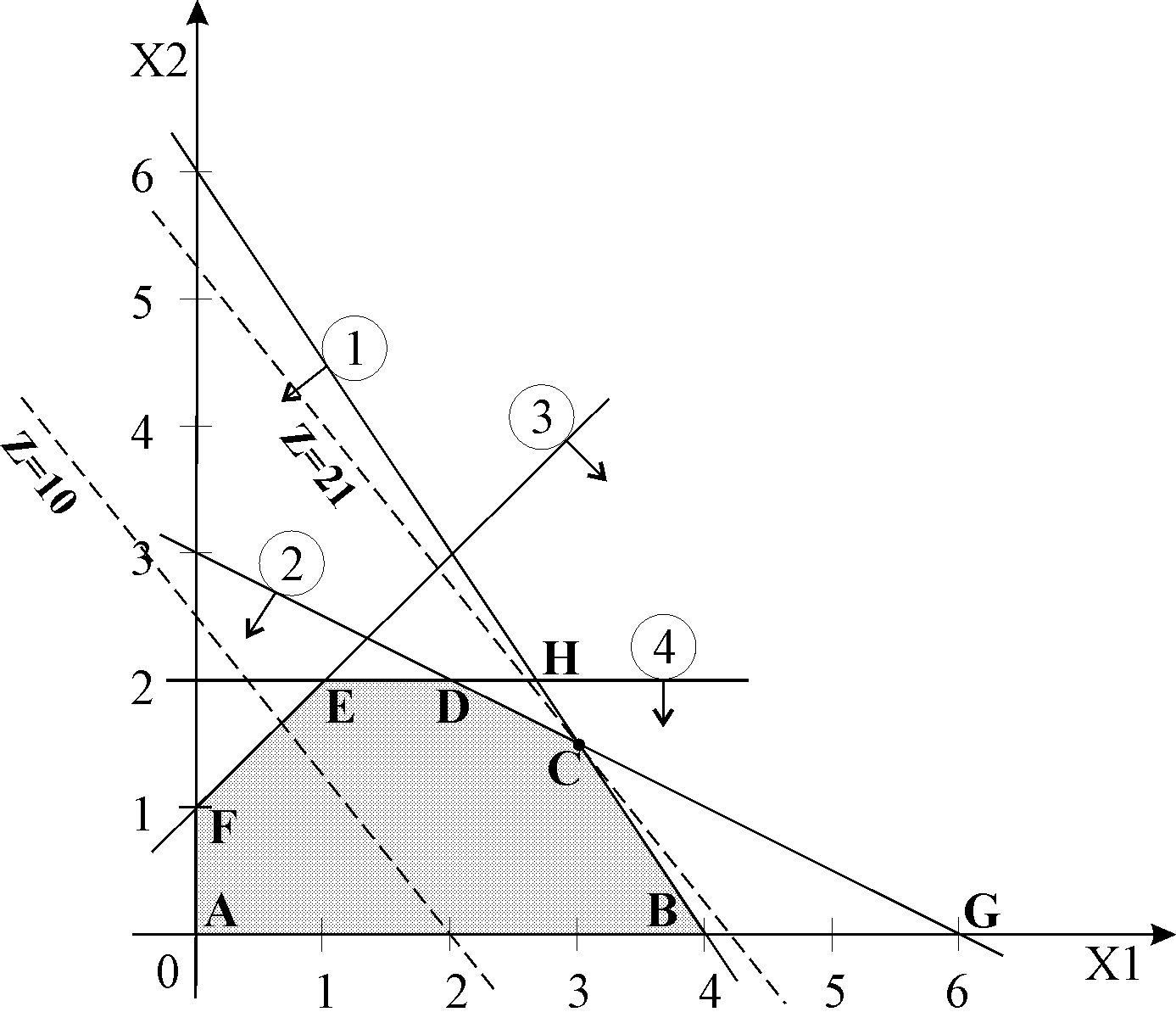
Рис. 1

3.3. Анализ чувствительности

После нахождения оптимального решения задачи линейного программирования естественно возникает вопрос изучения влияния изменения параметров модели на полученное оптимальное решение. Такое исследование называется анализом чувствительности.

Анализ модели на чувствительность позволяет дать ответы на следующие вопросы:

1. Можно ли увеличить запас некоторого ресурса для улучшения полученного оптимального значения целевой функции? На сколько можно увеличить запас этого ресурса?

2. Можно ли снизить запас некоторого ресурса при сохранении полученного значения целевой функции? На сколько можно снизить запас этого ресурса?

3. Увеличение объема какого из ресурсов наиболее выгодно?

4. В каких пределах могут меняться коэффициенты целевой функции при условии неизменности оптимального решения?

Первые три пункта соответствуют анализу модели на чувствительность к правым частям ограничений (запасам ресурсов), последний — на чувствительность к коэффициентам целевой функции (ценам).

Рассмотрим анализ чувствительности, основанный на графическом решении задачи.

Ограничение называется активным, если в точке оптимального решения оно выполняется как равенство. Прямая, соответствующая активному ограничению, должна проходить через оптимальную точку.

Ограничение называется неактивным, если в точке оптимального решения оно выполняется как строгое неравенство.

Ресурс называется дефицитным, если соответствующее ему ограничение является активным. Аналогично ресурс называется недефицитным, если соответствующее ему ограничение является неактивным.

Таким образом, при анализе модели на чувствительность к правым частям ограничений можно определить:

1) предельно допустимое увеличение запаса дефицитного ресурса, позволяющее улучшить найденное оптимальное решение,

2) предельно допустимое снижение запаса недефицитного ресурса, не изменяющее найденного ранее оптимального решения.

Для того чтобы определить предельно допустимое увеличение запаса дефицитного ресурса необходимо определить то предельное положение, после которого соответствующее ограничение становится избыточным.