1. Инф-ия. Виды и св-ва инф. ИП и ИТ

Пон-ие инф-ии явля-ся фунд. пон-ем в любой науке вообще и базовым в И. Формаль-го опр-ия не имеет. Каждая наука рассм. это понятие со своей стороны. В филос-ии под инф-ей понимают отражение реального мира. Инф. м/о классиф-ть по: форме, структуре, способу передачи и восприятия (обмену), области возникновения. С пон-ем инф-ии связаны след-ие пон-ия: 1) Сигнал - представл-ий собой любой физ. процесс, несущий инф-ию. 2) Сообщение - инф-ия, представл-ая в опред-ой форме и предназ-ая для передачи. 3) Данные - инф-ия, представл. в формализованном виде и подготовленная для обраб-ки технич-и устр-ми.

Инф-ия может перед-ся сигналами 2-ух типов: непрер-ый (парам-ры сигнала м. принимать любые зн-ияиз данного диапазона); дискретный (пар-ры сигнала приним-ют конечное число знач-ий из данного диапазона).

Инф-ия, предст-ая в любой форме, - это отражение окр-го нас мира с помощью знаков и сигналов. Отражение д/но быть правдивым и не искажать оригинала, а для этого она д/на обладать такими необх-ми св-ми как достоверность и полнота, ценность и актуальность, ясность и понятность.

Ед. измер. инф-ии. Сущ. 2 подхода: вер-ый и объемный. 1) Кол-вом инф-ии наз-ют числ. хар-ку сигнала, отраж-ую ту степень неопр-сти, кот. исчезает после пол-ия сигнала. Под единицей инф-ии понимают такое ее кол-во, кот. уменьшает неопредел-сть в 2 раза. Ед-ца изм. инф. - бит. N - кол-во событий, i - кол-во инф-ии N=2ⁱ ; I=log₂N.Если кол-во равновер-ых соб-ий = N, то кол-во инф-ии i, полученное при выпадении этого соб-ия, м/б выч-но по фор-ле Хартли i=log₂N. За ед-цу инф-ии в сист. СИ принимают 1 байт=8 бит. 2) Объем инф-ии в памяти ЭВМ или на носителе равен кол-ву бит.

ИП. Действия выпол-е с инф-ей наз инф. процеессами. К ИП относят сбор, обраб-ку, хранение и обмен инф-ей. Сбор инф-ии - деят-сть, в ходе кот. пол-ют сведения об интересующем объекте. М. осущ-ся как чел-ком, так и аппаратно. Обработка – упорядоченный процесс ее преоб-ия в соотв-ии с нек-ым алгоритмом. Хранение – процесс поддержания инф-ии в виде обеспечивающем выдаче конечных данных по запросам пользователей в установл-ые сроки. Обмен - процесс, имеющий две формы: передача, прием. Обяз-но присутств-ют источник и приемник инф-ии и среда передачи инф-ии. Матер-ый носитель - сигнал. (пример сх. Шеннона).

ИТ - процессы, испол-ие сов-сть ср-в и м-дов для обеспечения ИП: сбора, обраб-ки и передачи данных (первичной инф-ии), для пол-ия инф-ии нового кач-ва о сост-ии объекта, процесса или явл-ия (инф. продукта). Цель ИТ - произ-во инф-ии для ее анализа чел-ком и принятия на его основе реш-ия по вып-ию к-л действия. Внедрение ПК в инф-ую сферу и прим-ие телекоммуникаций опред-ли новый этап раз. инф. технологий. НИТ - ИТ с «дружественным» интерфейсом р-та пользователя, исп-ая ПК и телекомм-ые ср-ва.

7. Разработка эффективных алгоритмов: методы «Разделяй и влавствуй» и динамическое программирование.

Одна из самых конструктивных идей состоит в разложении задачи “размерности” n на одну операцию некоторой сложности, например, O(n) или O(1), и похожую задачу размерности m, меньшей n, или в общем случае на k задач с размерностями m₁, m₂, …, m_k таких, что m₁+ m₂ + …+m_k £n. Эта идея открывает путь к решению многих задач. Из нее исходят, в частности, почти все методы сортировки.

Теорема 1. Пусть a, b, c – неотрицательные постоянные. Решение рекуррентных уравнений

где n - степень числа c, имеет вид:

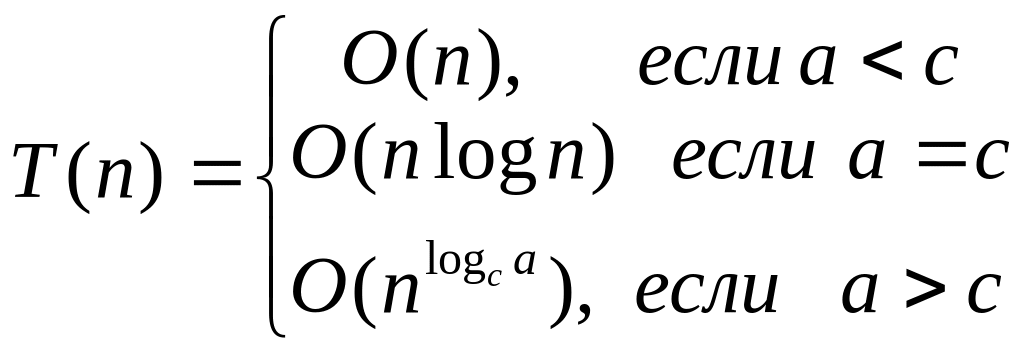
Из этой теоремы вытекает, что разбиение задачи размера n (за линейное время) на две подзадачи размера n/2 дает алгоритм сложности O(nlogn): a = c = 2. Если бы подзадач было 3, 4 или 8 (c=2, a=3>2, a=4>2, a=8>2 ), то получился бы алгоритм сложности порядка n^log3, n² и n³ соответственно.

С другой стороны, разбиение задачи на 4 подзадачи размера n/4 дает алгоритм сложности O(nlogn): a = c = 4. Если бы подзадач было 9 и 16 (c=4, a=9>4, a=16>4) – порядка n^log3 и n² соответственно.

Поэтому асимптотически более быстрый алгоритм умножения целых чисел можно было бы получить, если бы удалось так разбить исходные целые числа на 4 части, чтобы суметь выразить исходное умножение через 8 или менее меньших умножений. Другой тип рекуррентных соотношений возникает в случае, когда работа по разбиению задачи на не пропорциональна ее размеру.

Динамическое программирование.

Подобно методу “разделяй и властвуй”, ДП решает задачу, разбивая ее на подзадачи и объединяя их решение. Алгоритмы типа “разделяй и властвуй” делят задачу на независимые подзадачи, эти подзадачи – на более мелкие подзадачи и т.д., а затем собирают решение основной задачи “снизу вверх”. ДП применимо тогда, когда подзадачи не являются независимыми, т.е. когда у подзадач есть общие “подзадачи”. В этом случае алгоритм типа “разделяй и властвуй” будет делать лишнюю работу, решая одни и те же подзадачи по несколько раз. Алгоритм, основанный на ДП, решает каждую из подзадач единожды и запоминает ответы в специальной таблице. Это позволяет не вычислять заново ответ к уже встречавшейся задаче.

При трассировке рекурсивного алгоритма вычисления, например, десятого числа Фибоначчи видно, что сначала мы должны вычислить девятое и восьмое числа и сложить их. При этом восьмое число Фибоначчи будет вычисляться и при вычислении девятого числа, но полученный результат будет забыт, а потом опять вычислен. При возрастании номера вычисляемого числа количество одинаковых вызовов будет лишь увеличиваться. Так, при подсчете десятого числа Фибоначчи третье будет вычисляться 21 раз.

Эффективность алгоритма можно значительно повысить, если заменить движение с конца к началу движением от начала к концу.

Очевидно, что для хранения последних двух элементов массива можно взять две вспомогательные переменные вместо того, чтобы хранить весь массив.

2. Общие принципы код-я информации и формы ее представления в эвм

Пр-п Фон-Неймана. В основу построения больш-ва комп-ров положены следующие общие принципы сформ-ные в 1945году Фон-Нейманом: п-п программного управ-я. Из него =>, что прогр-ма состоит из набора команд, кот-е выпол-ся процессором авто-ки друг за другом в опред-ой послед-сти. Выборка программ из памяти осущ-ется с помощью счетчика команд. П-п однородности памяти. Прог-мы и данные хранятся в одной и той же памяти комп-р не различает что хранится в данной ячейке: прог-ма, число, текст или команда. Над ком-ми м. выполнять такие же действия, как и над данными. П-п адресности. Структурно осн. память состоит из перенумерованных ячеек. Проц-ру в произвольный момент t доступна любая ячейка, следовательно сущ-ет возмо-ть давать имена областям памяти так, чтобы к заполненным в них знач-ям м. было в последствии обращаться или менять их в процессе выполнения прог-мм с испол-ем присвоенных имен. Запись инф-ции. ОЗУ ЭВМ состоит из физических устройств элементов памяти - битов, способных устойчиво нах-ся в одном из состояний условно обознач-х 0 и 1. Каж. элемент хранит один бит инф-ции. Исторически сложилось 8 бит = 1 байту, ко-й в соврем. Вычис-х сис-х явл-ся мин-ой адрес-ой областью памяти. Байты м. объед-ся в машинные слова. Маш. слово имеет адрес младшего байта. Рассмотрим принципы код-я инф-и в 2-х байтовых словах. Кодирование целых чисел.

+ые числа. В стар-й бит запис-ся 0, в остальные разряды запис-тся 2-ое предст-ие числа, начиная с младшего бита. Своб-ые левые разряды запол-ся 0.

–ые числа. Код-е + чисел наз-ся код-ем в прямом коде. - числа принято код-ть в допол-ном коде. Его м. получить по след-му алгоритму: двоичное предст-ние модуля числа инвертируют, т.е. 10, а 01. К получен-му прибавляем 1.признаком отр. числа является 1 в старшем бите. Восстановить число м. по тому же алгоритму. Все выше изложенное применимо к целым со знаком, для целых без знака не происходит резервирование бита под знак. Код-ие символов. В совр. Выч-ых сис-х каждому сим ставят в соотв-ии нек. число назыв-ое кодом символов. Код-ые символы состоят из групп: управляющие, цифры, латинские буквы и специальные символы. Су-ет несколько стандартов код-ия. Большинство современных ВС используют стандарт ASCII в кот-ом каж. символ кодируется в один байт. Т.е. можно закодирова-ть 256 сим-в кодами от 0 до 255. Сим-ы с кодами от 0 до 127 явл-ся стандар-ми, а с кодами от 127 до 255 явл-ся переменной частью кодовой таблицы и м. включать символы нац. алфавита, псевдографики. Истор-ки для больших ЭВМ первым был разработан стандарт EBC DIC занимал 12 бит. В наст. вр разработана сис-ма код-я в 2 байта – UNICOD. Может закод-ть 2¹⁶-1 символ. Код-ние команд. Коды к-д записывают в два поля, одно из кот-ых (обычно 1 байт) код-т код операции, второе наз-тся адресным. В зав-сти от ВС ком-ы бывают: без-,одно-,двух-, трех-, четырехадресные. В адресной части могут хранится: ад-са двух операндов, ад-с следующей ком-ы, адрес результата. Для экономии памяти часто исп-ют 2-х адр-ые ком-ы, кот-ые хранят лишь ад-са операндов, а рез-ат запис-ся по адресу одного из операндов. Код-ние графической информации. Код-ие растр-х изобр-ний. Растр изоб-е предст-ет собой совокуп-ь точек (пикселей) разн. цветов(BMP, GIF и JPEG). В формате BMP задается цветность всех пикселов изоб-я. Этот формат требует много памяти. В формате GIF исп-ся спец. методы сжатия кода, причем поддер-ся только 256 цветов. Формат JPEG исп-ет методы сжатия, приводящие к потерям нек-х деталей.Кодирование векторных изображений. Вект. Изоб-е пред-ет собой совокуп-ть граф-х примитивов (точка, отрезок, эллипс…). Каж примитив описывается мат. формулами. В век графике, в отличие от раст графики, базовым объектом явл-ся линия. фрактальная графика, в ко-й формир-ие изо-ий целиком основано на мат формулах, уравн-х, описывающих те или иные фигуры, поверх-и, тела. Двоичное код-ие звука. Подход к записи звука наз-ся преобр-ем в цифровую форму, оцифровыванием или дискретизацией, так как непрер-й звуковой сигнал замен-ся дискретным набором знач-й сиг-ла в нек-ые моменты вр-ни. Кол-во отсчетов сигнала в единицу t наз-ся частотой диск-ации. В нас время при записи звука в мульт-х технях прим-ся частоты 8, 11, 22 и 44 кГц.

Кодирование и декодирование.

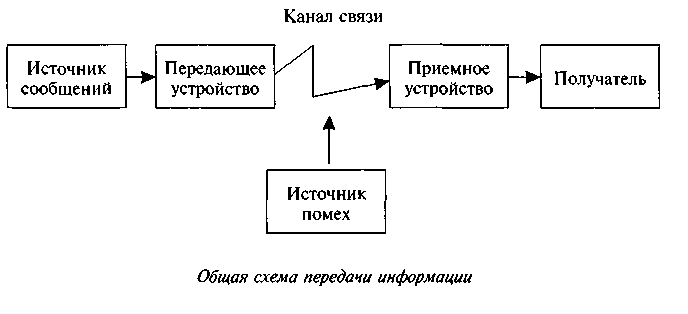
В канале связи сое, состав-е из символов (букв) одного алф-а, м. преобр-ся в сооб-е из сим-ов (букв) др. алфавита. Правило, описывающее однозначное соотве-ие букв алфавитов при таком преоб-ии, наз-ют кодом. Саму процедуру преобр-ия сооб-я наз-ют перекодировкой. Подобное преобр-ние сооб-я м. осущ-ся в момент поступления сооб-я от ист-ка в канал связи (код-ние) и в момент приема сооб-я получ-лем (декод-е). Устр-ва, обеспеч-щие код-е и декод-е, будем наз-ть соответ-нно код-щиком и декод-ком. На рис. 3 приведена схема, иллюстрирующая процесс передачи сообщения в случае перекодировки, а также воздействия помех.

Понятие о теоремах Шеннона. Теоремы Шеннона затрагивают проблему эффективного кодирования. Первая теорема декларирует возможность создания системы эффективного кодирования дискретных сообщений, у которой среднее число двоичных символов на один символ сообщения асимптотически стремится к энтропии источника сообщений (в отсутствии помех). Вторая теорема Шеннона гласит, что при наличии помех в канале всегда можно найти такую систему кодирования, при которой сообщения будут переданы с заданной достоверностью.Международные системы байтового код-ния. Наиболее распрост-ны две такие системы: EBCDIC (Extended Binary Coded Decimal Interchange Code) и ASCII (American Standard Information Interchange).

3. Основы анализа алгоритмов. Асимптотическая временная сложность алг-мов. Классификация скоростей роста сложности алг-ма. О-символика. Полиномиальные, экспоненциальные и факториальные алг-мы. Классы N и NP.

Для оценки эф-ти алг-ов введено понятие сложности алг-ма. Вычисл.процессом, порожденным алг-ом, н-ся послед-ть шагов алг-ма, пройденных при исп-ии этого алг-ма. Слож-ть алг-ма- это кол-во элем-ных шагов в вычислит.процессе этого алг-ма. Временная слож-ть алг-ма – это время Т, необх-ое для его вып-ия в зав-ти от исх.д-ых. Оно равно произв-ю числа элем-ых действий k на среднее время вып-ия 1го действия t: T=kt. Емкостная слож-ть опред-ся числом занятых ячеек памяти и не м.б. больше C_i (1<i<k), где C_i – кол-во ячеек, занятых на i шаге. Если положить С=maxC_i , то C_i <=C*k, т.е. и емкостную слож-ть м.свести к временной.

Для анализа алг-ов исп-ся еще 1 подход, основанный на подсчете времени работы алг-ма при возрастании размерности задачи, т.е. на вычислении асим-ой эф-ти алг-та. Асимптотика - это искусство оценивания и сравнения скорости роста ф-ций (обозн. О-символика).

Время вып-ия алг-ма А прямо пропорц-о ф-ции f(n). Если время реш-я задачи прямо пропорц-о ее размеру n, то сложн-ть задачи = О(n), т.е. имеет порядок n. Если время реш-я задачи прямо пропорц-о квадрату ее размера n², то сложн-ть задачи = О(n²) Точное знание кол-ва операций, вып-ых алг-ом, не играет существ-ой роли, важно знать скорость роста этого числа при возрастании объема входных д-ых. Оно н-ся скоростью роста слож-ти алг-ма.

Пусть f- нек-ая ф-ция. Алг-мы м. сгруппировать по скорости роста их сложн-ти:

1) алг-мы, слож-ть к-ых растет по кр.мере так же быстро, как дан.ф-ция f;

2) алг-мы, слож-ть к-ых растет с той же скоростью, что и дан.ф-ция f;

3) алг-мы, слож-ть к-ых растет медленнее, чем дан.ф-ция f.

Омега большое. Класс ф-ций, растущих по кр.мере так же быстро, как g, обозн. ч\з (g). Ф-ция, f(g), если при всех знач-ях арг-та n_0, и нек-го полож-го с вып-ся нерав-во f(n)>c g(n). М. считать, что класс (g) задается указанием своей нижней границы: все ф-ции этого класса растут по кр.мере так же быстро, как g.

О большое. Оценка О треб-ет только, что бы ф-ция f(n) не превышала g(n) начиная с n>n_0, с точностью до постоянного множителя. Класс ф-ций, растущих не быстрее, чем g, обозн. ч\з О(g). Ф-ция, fО(g), если при всех знач-ях арг-та n_, больших нек-го порога n₀, и нек-ого полож-го с вып-ся нерав-во f(n)<=c g(n).

Тета большое. f(n)=(g(n)), если сущ-ют полож-ые с1,с2,n0, такие, что: с1*g(n)<=f(n)<=c2*g(n), при n>n0. Ч\з (g) обоз-им класс ф-ций, растущих с той же скоростью, что и g. Этот класс явл-ся пересечением 2х предыд.

Полиномиальным алг-мом (или алг-м полиномиальной временной слож-ти) н-ся алг-м, у к-го временная слож-ть =О(Р(n)), где Р(n) – нек-ая полиномиальная ф-ция от входной длины n. Алг-мы, для временной слож-ти к-ых не сущ-ет такой оценки, н-ся экспоненциальными.

Все задачи, для реш-я к-ых имеются алг-мы полином-ой слож-ти, составляют класс Р – класс задач полином. слож-ти. Такие задачи н-ся также практически разрешимыми. Сущ-ет и др.класс задач: они практически неразрешимы, и мы не знаем алг-ов, способных решить их за разумное время. Эти задачи образуют класс NP – класс задач недетерминированной полиномиальной сложн-ти. Др. словами NP – класс задач, к-ые м.решить за полиномальное время с пом. недетерминированных алг-ов (т.е. недетерм-ыми алг-мами, в к-ых всегда есть путь успешного вычисления за время, полномиальное отн-но кол-ва входных д-ых). Сложн-ть всех известных детермин-ых алг-мов, решающих эти задачи, либо экспоненциальна, либо факториальна.Сложн-ть нек-ых из них = 2ⁿ, где n- размерность задачи (кол-во входных д-ых).

Детерм-ый алг-м в каждый момент времени м.делать только что-то одно. В недетерм-ом алг-ме м.б. больше одного допустимого след.состояния.

Словосочет-е «недетерм. полиномиальный», характ-щее задачи из класса NP, объясняется след.двухшаговым подходом к их реш-ю. На 1ом шаге имеется недетерм-ый алг-м, генерирующий возм-ное реш-е такой задачи – что-то вроде попытки угадать реш-е. Иногда такая попытка оказывается успешной, и мы получаем оптим-й или близкий к оптим-ому ответ, иногда безуспешной. На 2ом шаге проверяется, действ-о ли ответ, полученный на 1 шаге, явл.реш-ем исходной задачи. Каждый из этих шагов в отд-ти требует полиномиального времени. Проблема в том, что мы не знаем, ск-ко раз нам придется повторить оба этих шага, чтобы получить иск. реш-е. Хотя оба шага и полиномальны, число обращений к ним м.оказаться экспоненциальным или факториальным.

Существует ряд важны практических причин для анализа ал­горитмов. Одной из них является необходимость получения оценок или границ для объема памяти или времени работы, которое потре­буется алгоритму для успешной обработки конкретных данных. Машинное время и память - относительно дефицитные (и дорогие) ресурсы, на которые часто одновременно претендуют многие пользователи. Хороший анализ способен выявить узкие места в программе, т.е. разделы программы, на которые расходуется большая часть времени. Существуют важные теоретические причины для анализа алгоритмов. Например, нужно иметь количественный критерий для сравнения двух алгоритмов, претендующих на решение одной и той же задачи, или для выявления наиболее эффективных и замены устаревших. Иногда нужно сделать аналогичные выводы о сравнительных достоинствах двух алгоритмов, из которых один может в среднем лучше работать на случайных входных данных, а другой -на каких-то специальных входных данных. Когда можно считать решение задачи оптимальным (т.е. алгоритм невозможно значительно улучшить). Для оценки качества алгоритма пользуются следующим критерием. Пусть А - алгоритм для решения некоторого класса задач, а n -размерность отдельной задачи из этого класса. В общем случае может быть массивом или длиной вводимой последовательности. Определим fA(n) как функцию, дающую верхнюю границу для максимального числа основных операций (сложения, сравнения и т.д.), которые должен выполнить алгоритм А для решения любой задачи размерности n. Говорят, что алгоритм А полиномиальный, если функция fA(n) растет не быстрее, чем полином от n, в противном случае алгоритм А экспоненциальный.