2.4 Скалярные произведения орт
Используя свойство 1 и формулу (10), можно найти скалярные произведения ортов осей координат:
,
.
2.5 Скалярное произведение в координатах
Если векторы
и
заданы своими координатами:
,
,
то скалярное произведение этих векторов
находится по формуле:
(12)
Условие
перпендикулярности векторов
и
в координатной форме можно записать:
(13)
Угол между векторами , заданными в координатной форме находится по формуле:
(14)
3 Векторное произведение
3.1 Определение скалярного произведения
Векторным
произведением вектора
на вектор
называется
третий вектор
,
определяемый следующими тремя условиями
(рис. 2):
1
,
где
- угол между векторами
,
.
2
,
(перпендикулярен плоскости векторов
и
).
3 Упорядоченная тройка векторов , , правая.
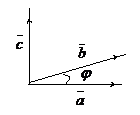
Рис.2
Векторное произведение обозначается:
или
Замечание
Упорядоченная тройка векторов
,
проведенных к общему началу, называется
правой, если с конца вектора
кратчайший
поворот вектора
к
вектору
виден
совершающимся против часовой стрелки
(правило правой руки). Если с конца
вектора
кратчайший
поворот вектора
к
вектору
виден
совершающимся по часовой стрелки, то
левой.
3.2 Алгебраические свойства векторного произведения
1
(не обладает переместительным свойством)
2
(сочетательный закон)
3
(распределительный закон)
3.3 Геометрические свойства векторного произведения
Из условия (1) определения векторного произведения следует условие (признак) коллениарности векторов.
1 Для того чтобы векторы и были коллениарны необходимо и достаточно, чтобы их векторное произведение было равно нулю.
(15)
2 Если векторы
и
приведены к общему началу, то модуль
векторного произведения
равен
площади параллелограмма, построенного
на векторах
и
(рис. 3).
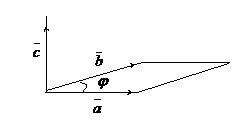
Рис. 3
(16)
3.4 Векторные произведения орт
Рассмотрим
векторное произведение
.
Принимая во внимание, что вектор
должен
быть перпендикулярен векторам i
и j и направлен
согласно правилу правой руки, легко
понять, что он совпадет с третьим базисным
вектором k, т.е.
.
Аналогично рассуждая
и
используя свойство
1 и формулу (15), можно найти векторные
произведения координатных ортов
(таблица
2).
Таблица 2
