Вариант 19

1. Изменить порядок интегрирования

.

2. Найти объем тела ограниченного поверхностями: .

3. Найти массу тела, ограниченного поверхностям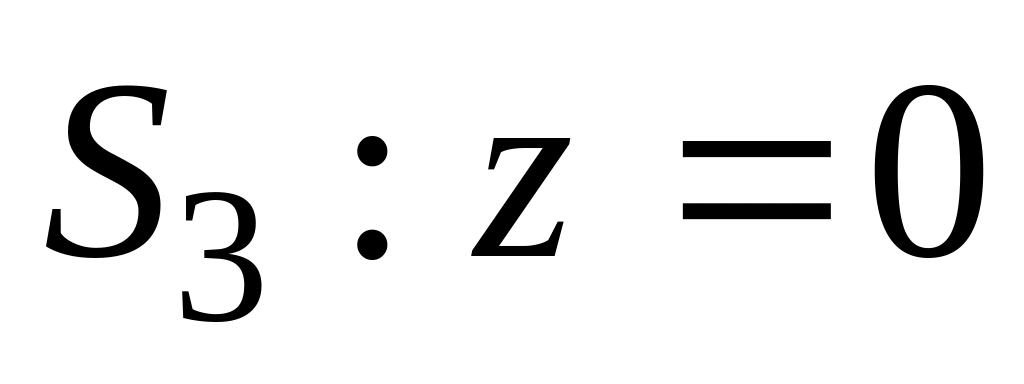и ; , если - плотность тела в точке.

4. Найти статический момент относительно плоскости 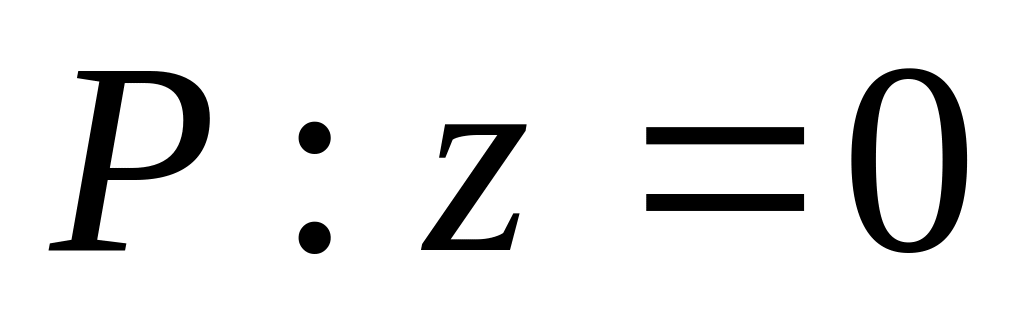однородного тела, ограниченного поверхностями ; ; .

5. Вычислить массу первого витка винтовой линии , если плотность в каждой ее точке .

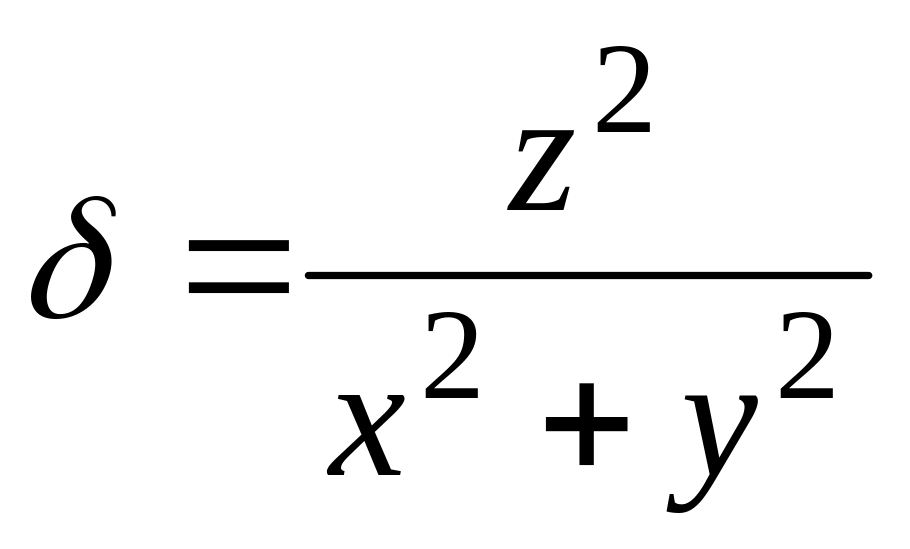6. Вычислить площадь участка поверхности при .

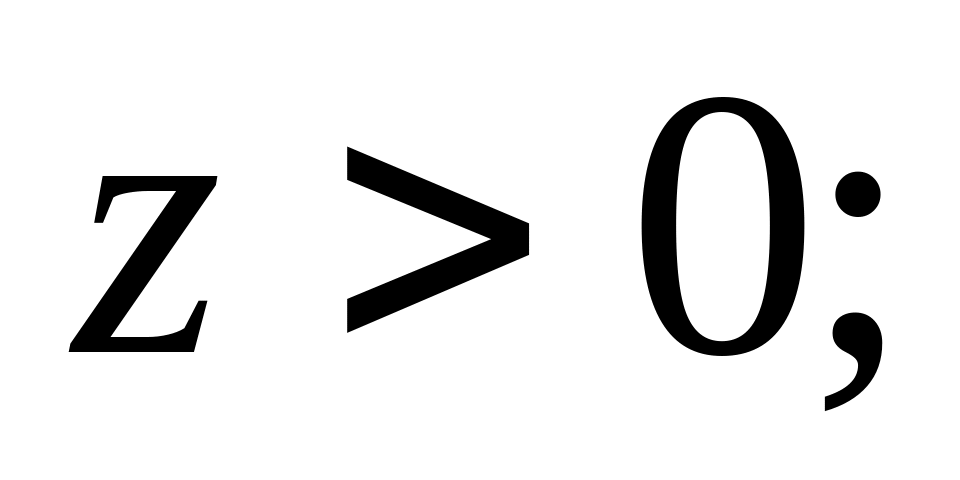
7. Найти производную скалярного поля в точке 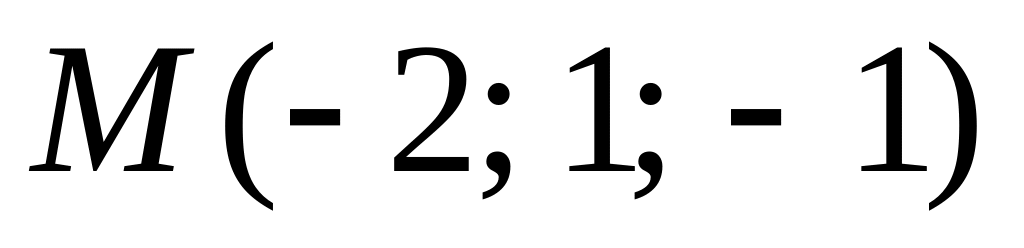по направлению вектора .

8. Найти работу поля вектора 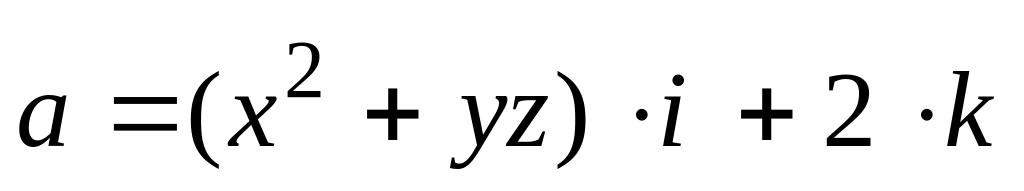при перемещении точки вдоль линии - отрезок MN, от точки к точке .

9. Найти поток векторного поля через замкнутую поверхность, ограниченную поверхностями в направлении внешней нормали (непосредственно и с помощью формулы Гаусса-Остроградского)

10. Найти циркуляцию вектора по контуру с помощью формулы Стокса и непосредственно (положительным направлением обхода контура считать то, при котором точка перемещается по часовой стрелке, если смотреть из начала координат).

11. Проверить потенциальность поля вектора 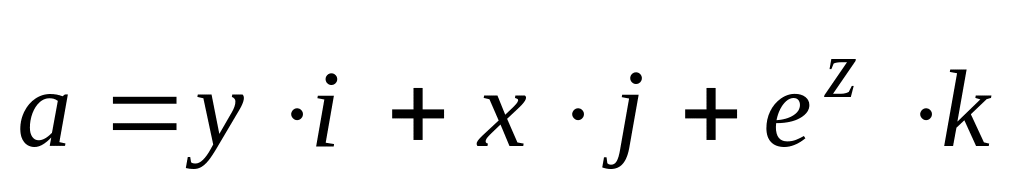, найти потенциал.

Вариант 20

1. Изменить порядок интегрирования

.

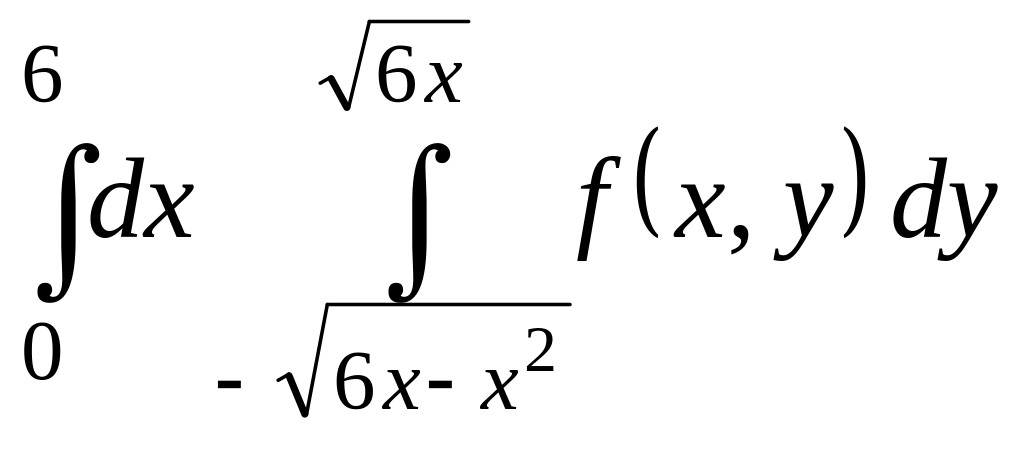2. Найти объем тела ограниченного поверхностями: .

3. Найти массу тела, ограниченного поверхностями , если 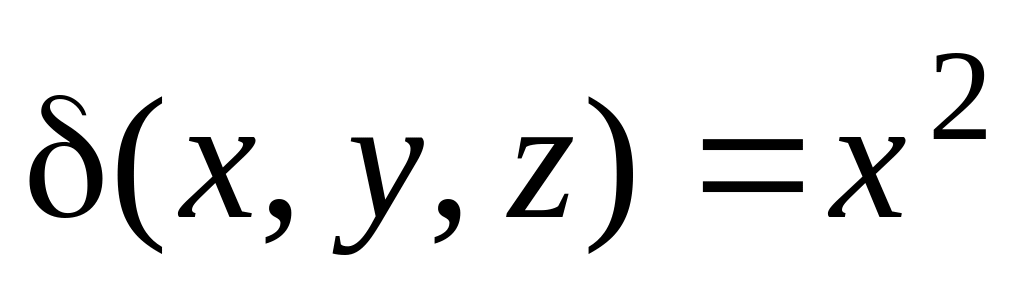- плотность тела в точке.

4. Найти статический момент относительно плоскости однородного тела, ограниченного поверхностями: и .

5. Найти центр тяжести однородной дуги окружности радиуса при центральном угле .

6. Вычислить массу части сферы , находящейся в первой октанте , если плотность в каждой ее точке равна расстоянию от точки до оси OZ.

7. Найти производную скалярного поля в точке по направлению вектора .

8. Найти работу поля вектора при перемещении точки вдоль линии - отрезок MN, от точки к точке .

9. Найти поток векторного поля 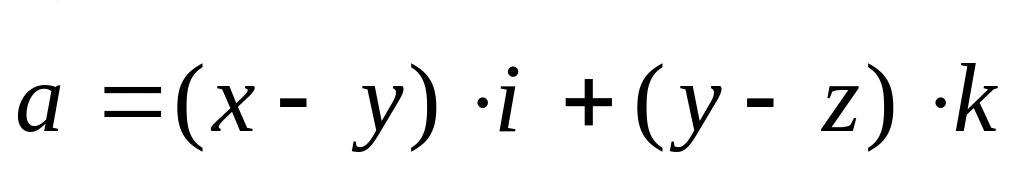через замкнутую поверхность, ограниченную поверхностями и в направлении внешней нормали (непосредственно и с помощью формулы Гаусса-Остроградского).

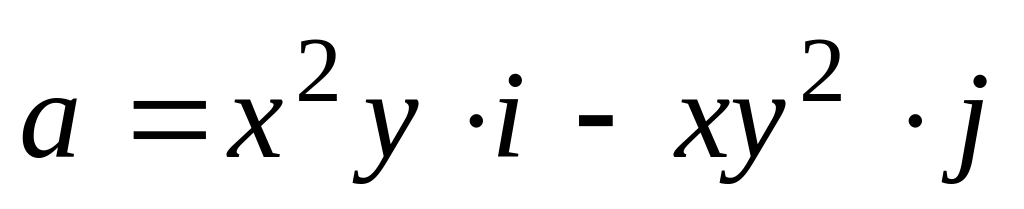10. Найти циркуляцию вектора по контуру с помощью формулы Стокса и непосредственно (положительным направлением обхода контура считать то, при котором точка перемещается по часовой стрелке, если смотреть из начала координат).

11. Проверить потенциальность поля вектора , найти потенциал.

Вариант 21

1. Изменить порядок интегрирования

2. Найти объем тела ограниченного поверхностями: .

3. Найти массу тела, ограниченного поверхностями , если - плотность тела в точке.

4. Найти статический момент относительно плоскости однородного тела, ограниченного поверхностями: ; .

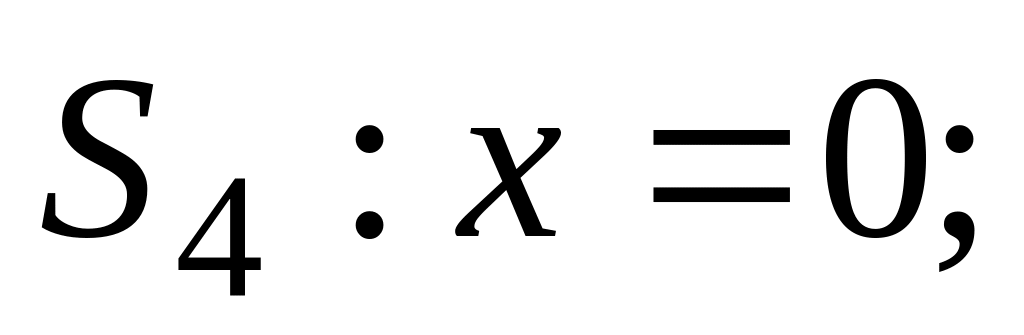
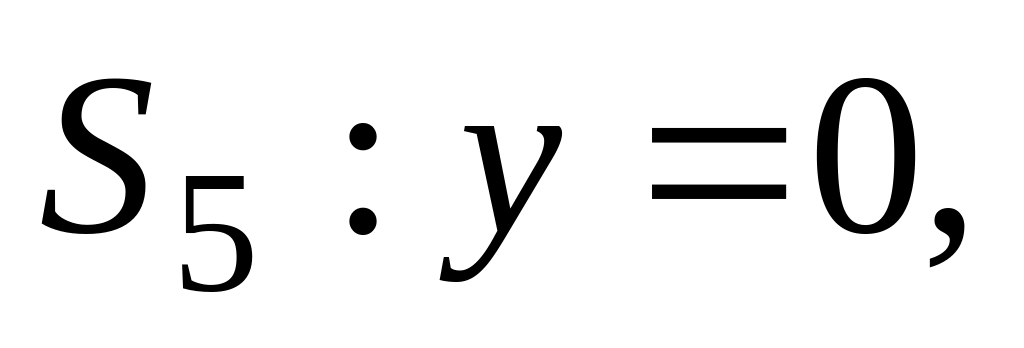
5. Вычислить массу прямолинейного стержня AB, где , если плотность в каждой его точке обратно пропорциональна расстоянию до начала координат.

6. Вычислить момент инерции относительно оси OZ однородной сферы 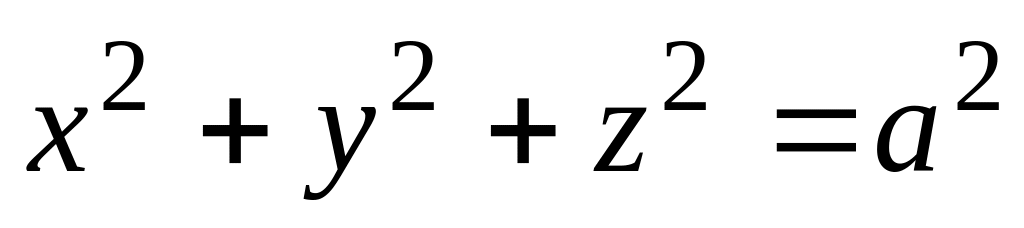, расположенной в первой октанте.

7. Найти производную скалярного поля в точке по направлению вектора .

8. Найти работу поля вектора при перемещении точки вдоль линии - отрезок MN, от точки к точке .

9. Найти поток векторного поля через замкнутую поверхность, ограниченную поверхностями 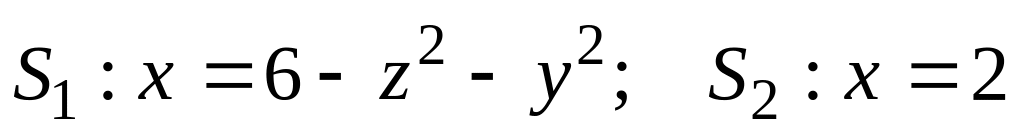в направлении внешней нормали (непосредственно и с помощью формулы Гаусса-Остроградского).

10. Найти циркуляцию вектора по контуру с помощью формулы Стокса и непосредственно (положительным направлением обхода контура считать то, при котором точка перемещается по часовой стрелке, если смотреть из начала координат).

11. Проверить потенциальность поля вектора , найти потенциал.