
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Проверить потенциальность поля вектора , найти потенциал.
Вариант 7
Изменить порядок интегрирования

Найти массу пластины, ограниченной линиями
 ,
если
,
если
 - поверхностная плотность пластины в
точке.
- поверхностная плотность пластины в
точке.
Найти объем тела, ограниченного поверхностями:

 (вне конуса).
(вне конуса).Найти центр тяжести однородного тела, ограниченного указанными поверхностями:
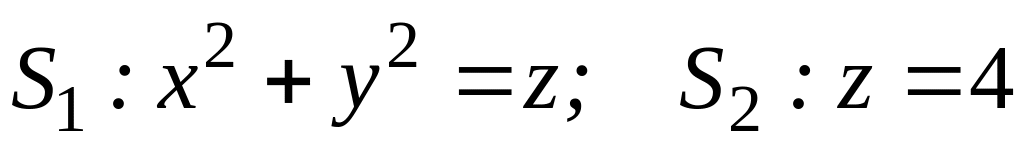 .
.Вычислить момент инерции относительно начала координат однородного первого витка винтовой линии
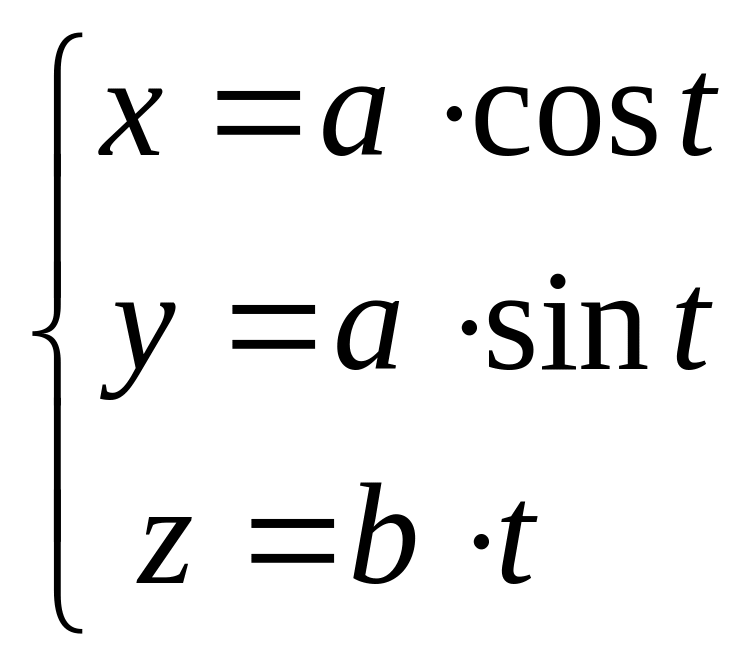 .
.Вычислить массу участка поверхности , отсеченной плоскостью
 ,
если плотность
,
если плотность
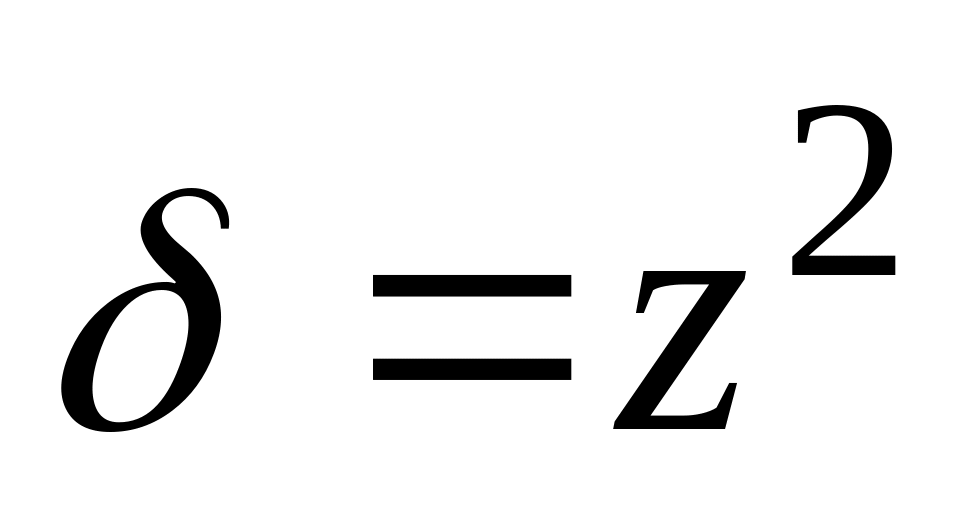 .
.Найти направление наибольшего возрастания функции
 в точке
в точке
 и скорость
ее возрастания в этом направлении.
и скорость
ее возрастания в этом направлении.
Найти работу поля вектора
 при перемещении точки вдоль линии
при перемещении точки вдоль линии
 L
от точки
L
от точки
 к точке
к точке
 .
.Найти поток векторного поля
 через часть поверхности
через часть поверхности
 ,
вырезанную плоскостью
,
вырезанную плоскостью
 непосредственно и с помощью формулы
Гаусса-Остроградского (нормаль внешняя
к замкнутой поверхности).
непосредственно и с помощью формулы
Гаусса-Остроградского (нормаль внешняя
к замкнутой поверхности).Найти циркуляцию вектора
 по контуру
по контуру
 с помощью формулы Стокса и непосредственно
(положительным направлением обхода
контура считать то, при котором точка
перемещается по часовой стрелке, если
смотреть из начала координат)..
с помощью формулы Стокса и непосредственно
(положительным направлением обхода
контура считать то, при котором точка
перемещается по часовой стрелке, если
смотреть из начала координат)..Проверить потенциальность поля вектора
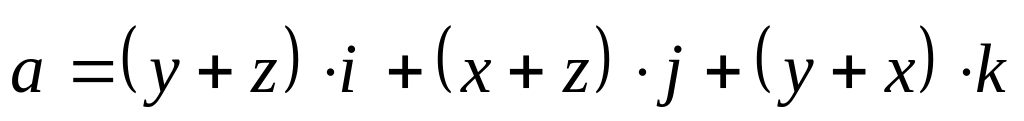 ,
найти потенциал.
,
найти потенциал.
Вариант 8
Изменить порядок интегрирования

Найти массу пластины, ограниченной линиями
 ,
если
,
если
 - поверхностная плотность пластины в
точке.
- поверхностная плотность пластины в
точке.
Найти объем тела, ограниченного поверхностями (между конусами)

Найти центр тяжести однородного тела, ограниченного указанными поверхностями

Вычислить массу части окружности
 в первой четверти, если плотность
в первой четверти, если плотность

Вычислить статические моменты однородной треугольной пластинки

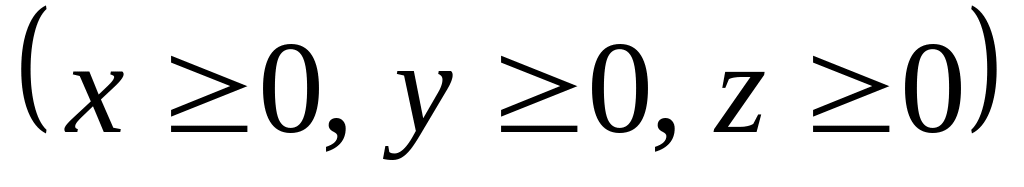 относительно координатных плоскостей.
относительно координатных плоскостей.Найти направление наибольшего возрастания функции
 в точке
в точке
 и
скорость ее возрастания в этом
направлении.
и
скорость ее возрастания в этом
направлении.Найти работу поля вектора
 при перемещении точки вдоль линии
при перемещении точки вдоль линии
 от точки
от точки
 к точке
к точке
 ,
где L -
ломаная, соединяющая точки
,
где L -
ломаная, соединяющая точки
 .
.Найти поток векторного поля
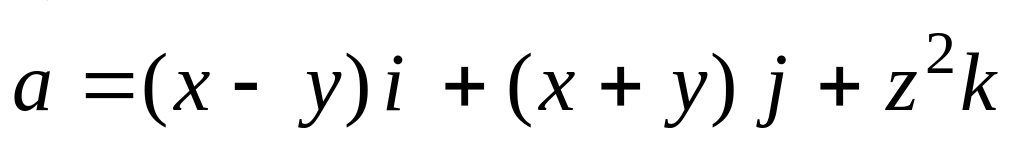 через часть поверхности
,
вырезанную плоскостями
через часть поверхности
,
вырезанную плоскостями
 непосредственно и с помощью формулы
Гаусса-Остроградского (нормаль внешняя
к замкнутой поверхности).
непосредственно и с помощью формулы
Гаусса-Остроградского (нормаль внешняя
к замкнутой поверхности).Найти циркуляцию вектора
 по контуру
по контуру
 с помощью формулы Стокса и непосредственно
(положительным направлением обхода
контура считать то, при котором точка
перемещается по часовой стрелке, если
смотреть из начала координат).
с помощью формулы Стокса и непосредственно
(положительным направлением обхода
контура считать то, при котором точка
перемещается по часовой стрелке, если
смотреть из начала координат).
Проверить потенциальность поля вектора
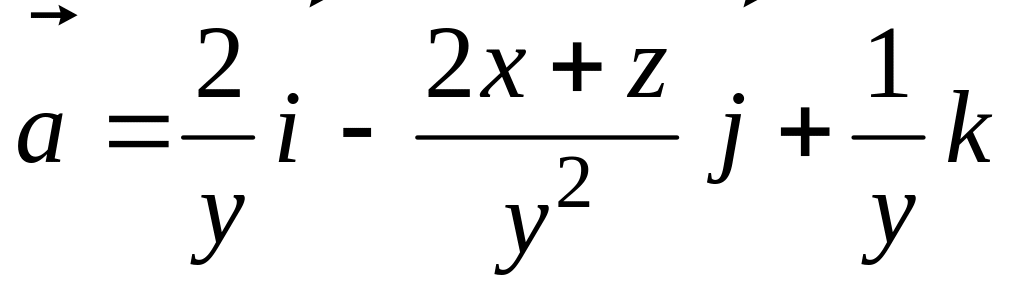 ,
найти потенциал.
,
найти потенциал.
Вариант 9
Изменить порядок интегрирования
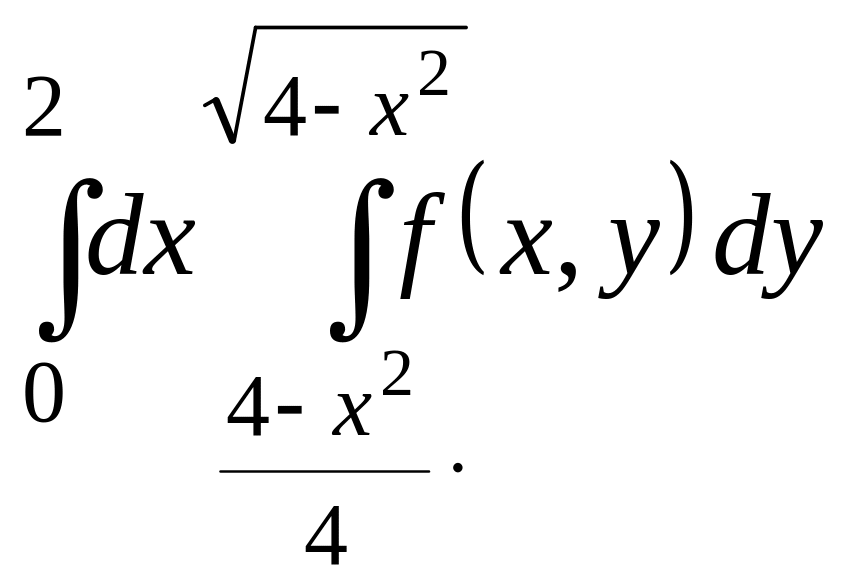
Найти массу пластины, ограниченной линиями
 ,
если
,
если
 - поверхностная плотность пластины в
точке.
- поверхностная плотность пластины в
точке.
Найти объем тела, ограниченного поверхностями:

Найти центр тяжести однородного тела, ограниченного указанными поверхностями:

Вычислить статический момент относительно оси OX однородного контура
 .
.
Вычислить массу участка поверхности
 ,
если плотность в каждой ее точке
,
если плотность в каждой ее точке
 .
.Найти направление наибольшего возрастания функции
 в точке
в точке
 и
скорость
ее
возрастания в этом направлении.
и
скорость
ее
возрастания в этом направлении.
Найти работу поля вектора
 при перемещении точки вдоль линии
от точки
к точке
,
где
L - ломаная,
соединяющая точки
при перемещении точки вдоль линии
от точки
к точке
,
где
L - ломаная,
соединяющая точки
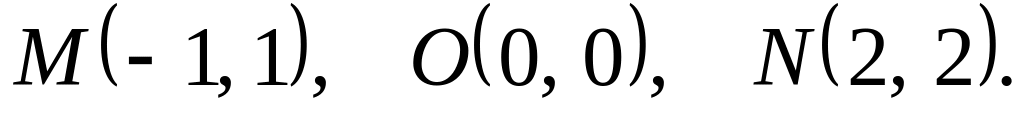 .
.Найти поток векторного поля
 через часть поверхности
,
вырезанную плоскостями
через часть поверхности
,
вырезанную плоскостями
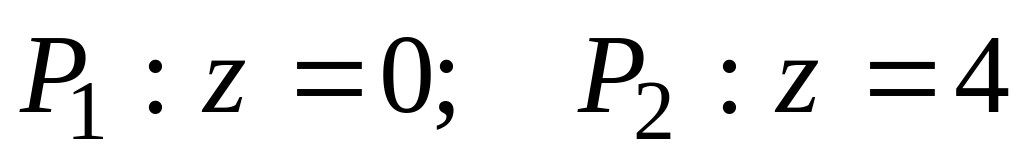 )
непосредственно и с помощью формулы
Гаусса-Остроградского. Нормаль внешняя
к замкнутой поверхности, образуемой
данными поверхностями.
)
непосредственно и с помощью формулы
Гаусса-Остроградского. Нормаль внешняя
к замкнутой поверхности, образуемой
данными поверхностями.
Найти циркуляцию вектора
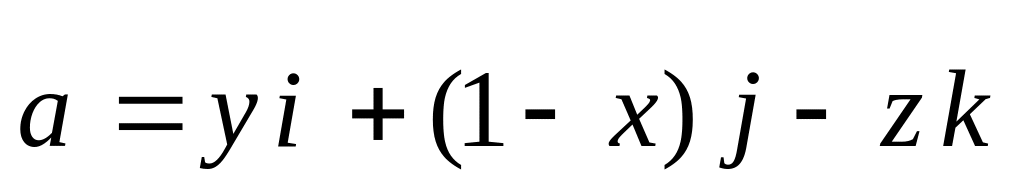 по контуру
по контуру
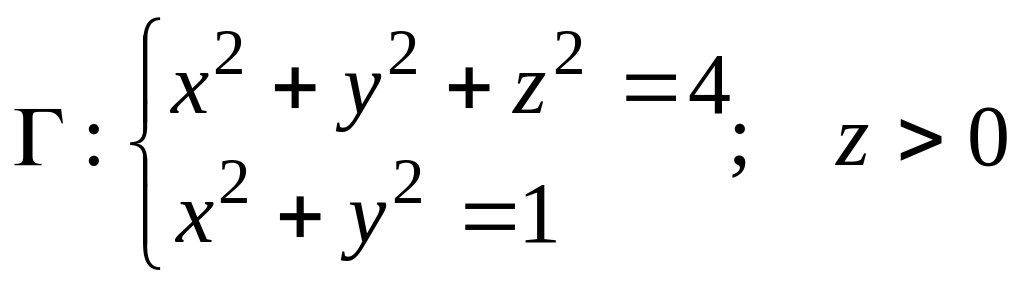 с помощью формулы Стокса и непосредственно
(положительным направлением обхода
контура считать то, при котором точка
перемещается по часовой стрелке, если
смотреть из начала координат).
с помощью формулы Стокса и непосредственно
(положительным направлением обхода
контура считать то, при котором точка
перемещается по часовой стрелке, если
смотреть из начала координат).
Проверить потенциальность поля вектора
 ,
найти потенциал.
,
найти потенциал.
