Вариант 19.

1. Вычислить частные производные и для функции .

2. Оценить абсолютную и относительную погрешности при вычислении значения функции .

3. Написать формулы для производных и для функции .

4. Вычислить все частные производные второго порядка для функции .

5. Вычислить дифференциал третьего порядка для функции .

6. Вычислить и для функции , заданной неявно .

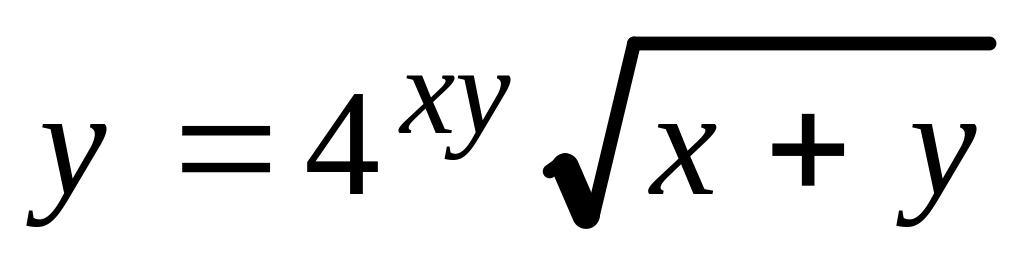7. Функция задана неявно зависимостью: . Вычислить частные производные и .

8. Функции и заданы параметрически: Вычислить частные производные , , и .

9. Написать уравнения касательной плоскости и нормали к поверхности, заданной уравнением 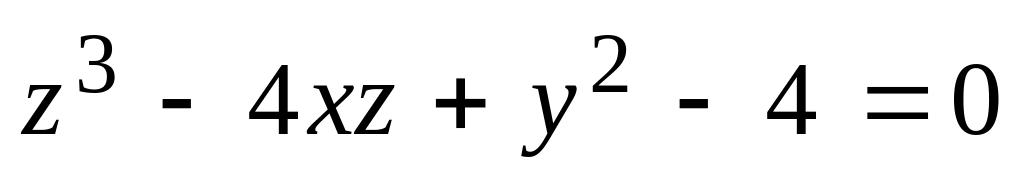в точке .

10. Исследовать функцию на экстремум.

11. Вычислить значения функции, заданной неявно зависимостью , во всех стационарных точках.

12. Найти наибольшее и наименьшее значения функции в области .

13. Из всех прямоугольников с заданной площадью найти такой, периметр которого имеет наименьшее значение.

Вариант 20.

1. Вычислить частные производные и для функции .

2. Оценить абсолютную и относительную погрешности при вычислении значения функции .

3. Написать формулы для производных и для функции .

4. Вычислить все частные производные второго порядка для функции .

5. Вычислить дифференциал для функции .

6. Вычислить и для функции , заданной: .

7. Функция задана неявно зависимостью: . Вычислить частные производные и .

8. Функции и заданы параметрически: 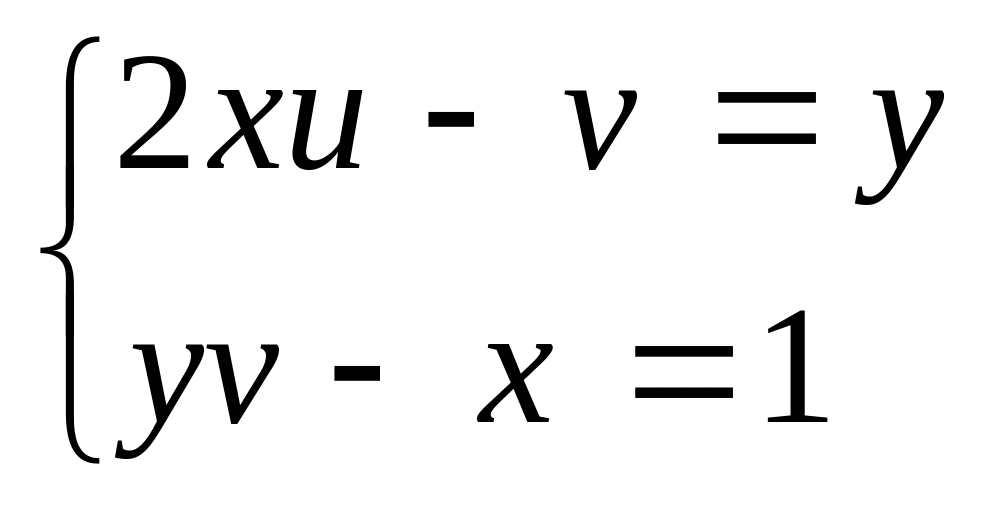Вычислить частные производные , , и .

9. Написать уравнения касательной плоскости и нормали к поверхности, заданной уравнением 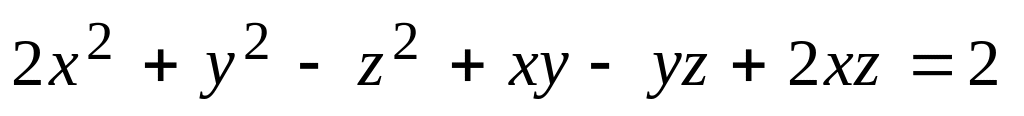в точке .

10. Исследовать функцию на экстремум.

11. Вычислить значения функции, заданной неявно зависимостью , во всех стационарных точках.

12. Найти наибольшее и наименьшее значения функции

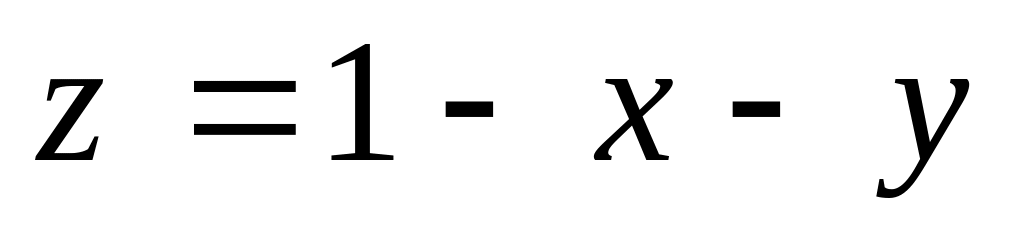
в области .

13. Из всех треугольников, имеющих данный периметр . найти наибольший по площади.

Вариант 21.

1. Вычислить и для функции .

2. Оценить абсолютную и относительную погрешности при вычислении значения функции при .

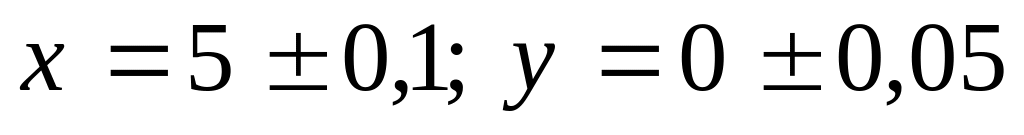3. Написать формулы для производных и для функции , при ,. , .

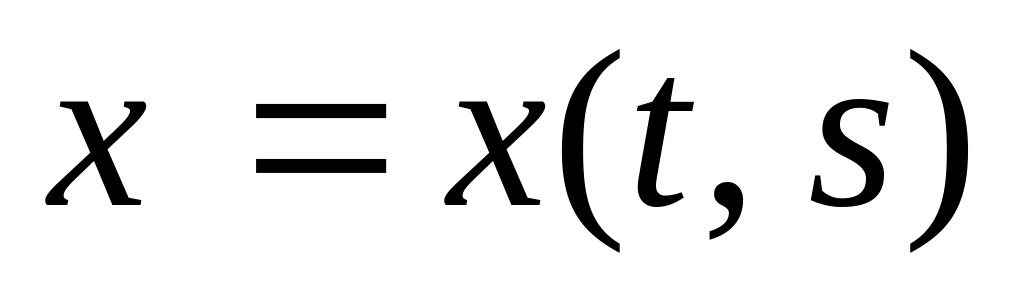4. Вычислить все частные производные второго порядка для функции .

5. Вычислить для функции .

6. Вычислить и для функции , если .

7. Функция задана неявно: . Вычислить частные производные и .

8. Функции и заданы параметрически: Вычислить частные производные , , и .

9. Написать уравнения касательной плоскости и нормали к поверхности, заданной уравнением в точке .

10. Исследовать функцию на экстремум.

11. Вычислить значения функции , заданной неявно зависимостью , во всех стационарных точках.

12. Найти наибольшее и наименьшее значения функции 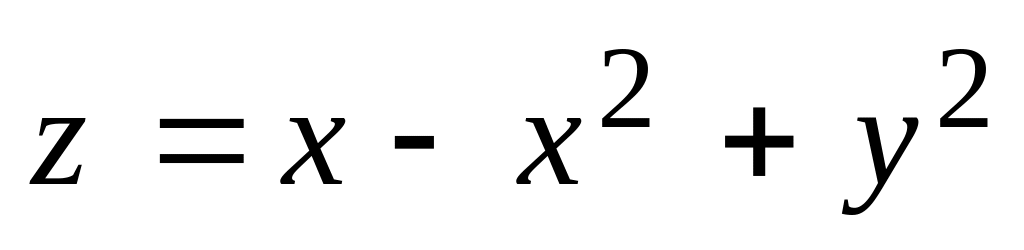в области .

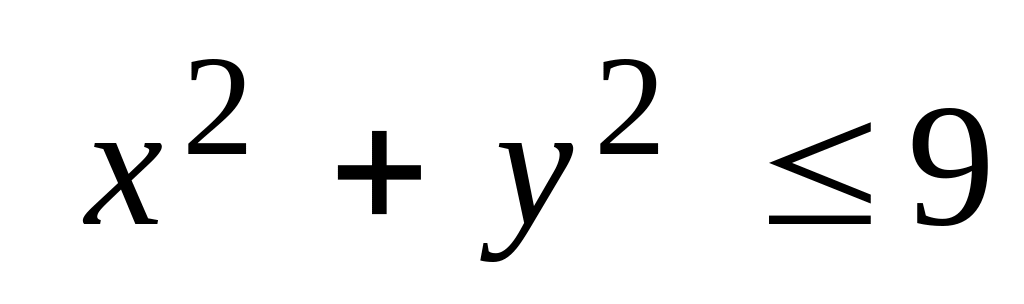13. На гиперболе найти точку, наименее удалённую от точки .

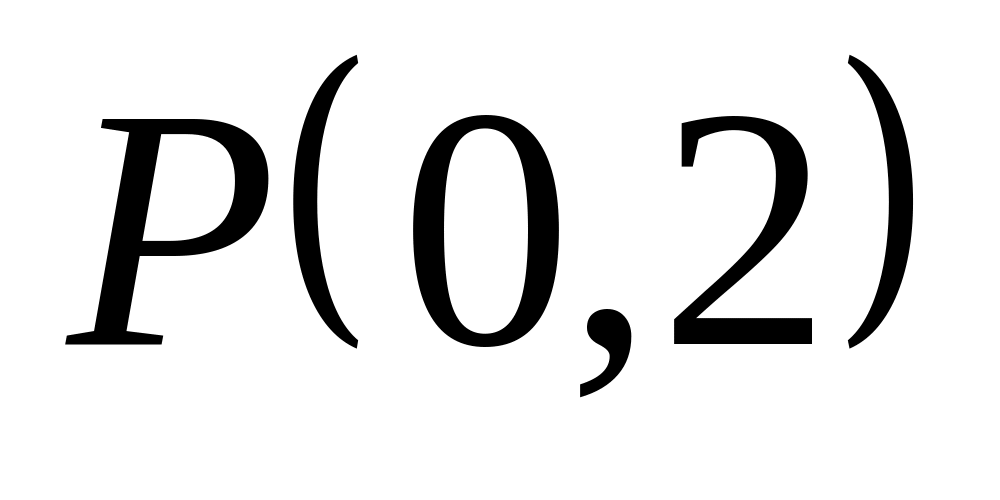Вариант 22.

1. Вычислить частные производные и для функции .

2. Оценить абсолютную и относительную погрешности при вычислении значения функции .

3. Написать формулы для производных и для функции .

4. Вычислить все частные производные второго порядка для функции: .

5. Вычислить дифференциал третьего порядка для функции .

6. Вычислить и для функции , заданной неявно:

7. Функция задана неявно: . Вычислить частные производные и .

8. Функции и заданы параметрически: . Вычислить частные производные , , и .

9. Написать уравнения касательной плоскости и нормали к поверхности, заданной уравнением в точке .

10. Исследовать функцию на экстремум .

11. Вычислить значения функции , заданной неявно зависимостью , во всех стационарных точках.

12. Найти наибольшее и наименьшее значения функции в области .

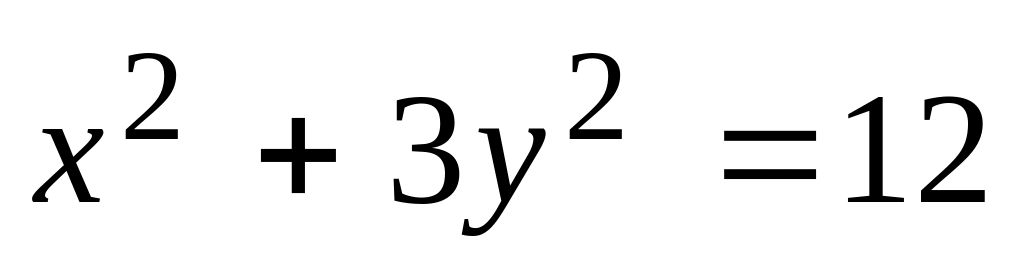13. В эллипс вписать равнобедренный треугольник с основанием, параллельным большой оси эллипса так, чтобы площадь треугольника была наибольшей.