%Определение логарифмических и амплитудно-фазовых характерист %Параметры скорректированной системы

h1=0.5*28.98; %Пропорциональная часть регулятора

h2=5*28.98*tf(1,[1,0]); %Интегральная часть регулятора

h3=h1+h2; %ПИ- регулятор

h5=tf(20,[0.01,1]); %Усилитель мощности.

h6=tf(5,[0.1,1]); %Объект регулирования.

h7=0.1 %Обратная связь.

h8=tf([0.003,1],[0.0001,1]); %Параллельная коррекция.

h=h3*h5*h6*h7*h8; %Передаточная функция разомкнутой системы.

%Параметры нескорректированной системы

w1=0.5; %Пропорциональная часть регулятора w2=5*tf(1,[1,0]); %Интегральная часть регулятора

w3=w2+w1; %ПИ- регулятор

w=w3*h5*h6*h7; %Передаточная функция разомкнутой системы

figure(1)

bode(h,w),grid on %ЛФЧ и ЛФЧ характриристики исследуемых систем.

figure(2)

nyquist(h,{100,4000}) %АФХ корректированной системы.

figure(3)

nyquist(w,{1,200}) %АФХ некорректированной системы.

figure(4)

x1=feedback(h,1); %Замкнутая скорректированная система.

x2=feedback(w,1); %Замкнутая нескорректированная система.

step(x1,x2),grid on %Переходные функции исследуемых систем.

В программе №1 определены логарифмические (рис.8) и амплитудно-фазовые характеристики (рис.9 и рис.10) структурных схем, представленных на рис.2А и рис.2С. Из рис.8 можно сделать вывод, который не виден в рассчетах. Быстродействие системы можно увеличить, увеличив коэффициент усиления. Из логарифмических характеристик следует, что запас по фазе увеличивается при

Рис.8. Логарифмические характеристики системы (1-скоректированная система; 2-нескоректированная система).

увеличении коэффициента усиления (допустимо увеличение коэффициента усиления в четыре раза), что прведет к увеличению частоты среза и, как следствие этого, к увеличению быстродействия.

Рис.9. Амплитудно-фазовая характеристика скоректированной системы.

Рис10. Амплитудно-фазовая характеристика нескоректированной системы.

Анализ характеристик, представленных на рис.8 - рис.10, позволяет установить важную закономерность, на которую редко обращают внимание в курсах теории автоматического управления, но которая достаточно подробно рассмотрена при рассчетах фильтров. Кривизна ФЧХ является фактором, который вызывает перерегулирование. Физически это объясняется тем, что кривизна ФЧХ вызывает разброс в задержках гармонических слагаемых, из которых состоит входной сигнал. Из-за этого различные слагаемые с разными фазами на входе (разные Фурье составляющие) приходят в некоторый момент к выходу в одной фазе, что вызывает перерегулирование. Сравнение логарифмических характеристик (рис.8) и амплитудно-фазовых характеристик (рис.9 и рис.10) показывает, что для скорректированной системы крутизна ФЧХ меньше, чем у нескорректированной системы, что и обеспечивает скорректированной системе меньшее перерегулирование.

Рис.11. Исследование чувствительности систем к изменению постоянных времени объекта при различных видах обратной связи

Уменьшение чувствительности выходных координат систем регулирования к изменению её параметров (стабилизационный эффект обратной связи) иллюстрируется структурными схемами, представленными на рис.11.

Рис.12. Переходные процессы, соответствующие структурным схемам рис.11

Рис.13. Исследование чувствительности систем к изменению коэффициента усиления при различных видах обратной связи

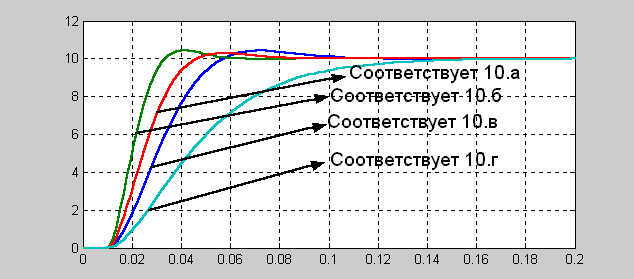
Рис.14. Переходные процессы, соответствующие структурным схемам рис.10

На рис.11.а и рис.11.б представлены схемы с последовательной и последовательно–параллельной коррекцией, настроенные на технический оптимум. На рис.11.в и рис 11.г представлена та же система, но с увеличенной в 2

раза постоянной времени объекта. Испытания (рис.12) показали, что в системе с последовательно–параллельной коррекцией изменение параметров системы (постоянной времени) меньше влияет на качественные показатели переходных характеристик.

На рис.13 представлены структурные схемы, позволяющие сравнить чувствительность систем с различными видами обратных связей при изменении коэффициента усиления разомкнутой системы. Системы (рис.13.а,13.б) настроены на технический оптимум. В системах (рис.13.в, рис.13.г) коэффициент занижен, по сравнению с оптимальным, в два раза. Причем, в системе (рис.13.в) применена комбинированная коррекция.

Из кривых, представленных на рис.14, следует, что отклонение коэффициента усиления от оптимального ухудшает качество переходных процессов. Однако в системах, использующих последовательно-параллельную коррекцию, ухудшение переходных характеристик выражено слабее.