§ 7 . Смешанное произведение векторов.
Смешанным произведением
векторов
называется число
,
равное скалярному произведению вектора
на вектор
:
.
Свойства смешанного произведения векторов:
Смешанное произведение равно нулю тогда и только тогда, когда один из векторов равен
,
или все три вектора параллельны одной
плоскости (компланарны).
2.
.
3. Смешанное произведение некомпланарных ненулевых векторов , по абсолютной величине равно объему параллелепипеда, построенного на векторах .
П
усть
,
,
.
Смешанное произведение в координатной форме имеет вид:
.
Докажем это утверждение.
Так
как
то, используя формулу для скалярного произведения, получим
Полученное выражение является разложением определителя третьего порядка по элементам третьей строки:
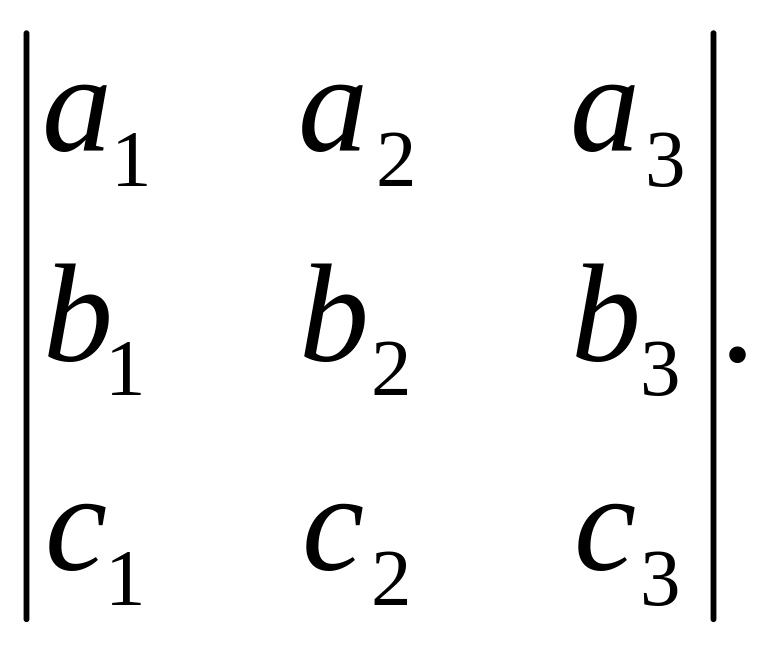
Условие компланарности векторов :
Пример.
Найти объем параллелепипеда, построенного на векторах :
,
,
.
Решение.
.
,
откуда окончательно имеем
.
Упражнения.
Даны три вектора
.
Вычислить
.Установить, компланарны ли векторы , если
1)
,
2)
.
3.
Доказать, что четыре точки
лежат в одной плоскости.
4.
Вычислить объем тетраэдра, вершины
которого находятся в точках
.
5. Даны
вершины тетраэдра:
.
Найти длину его высоты, опущенной из вершины D.
§ 8. Прямая на плоскости.
Уравнение
прямой
по заданным точке
и угловому коэффициенту
(где
- угол между прямой и осью
):
.
Уравнение прямой с
угловым коэффициентом
.
Если
,
то прямая
параллельна оси
и ее уравнение имеет вид
.
Уравнение прямой,
проходящей через две заданные точки
и
:
.
При равенстве нулю одного из знаменателей условимся считать равным нулю и соответствующий числитель.
Уравнение прямой по
точке
и направляющему вектору
:
.
Общее уравнение прямой
.
а) при
прямая проходит через начало координат;
б) при
прямая параллельна оси
;
в) при
прямая параллельна оси
;
г) при
-
ось
;
д) при
- ось
.
Уравнение прямой в отрезках на осях :
,
где a и b – величины отрезков, отсекаемых прямой на осях координат.
Задачи.
Построить прямую, отсекающую на оси
отрезок
и составляющую с осью
угол
.Построить прямую, проходящую через начало координат и точку
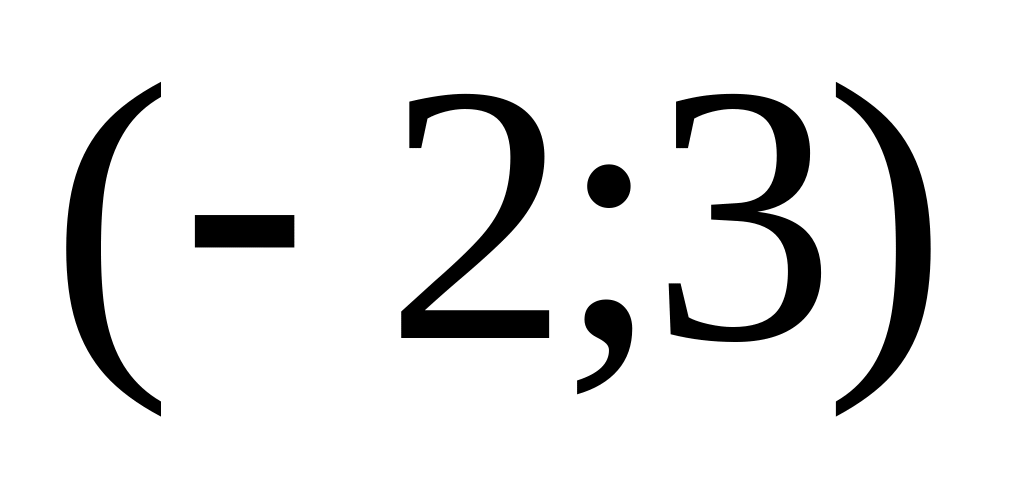.Определить параметры k и b для каждой из прямых :
1)
; 2) ; 3)
; 4)
.
Построить прямые :
1)
; 2)
; 3)
; 4)
.
5. Уравнения прямых :
1)
; 2)
,
привести к виду в отрезках на осях.
6
.Определить, какие из точек
лежат на прямой
и какие не лежат на ней.
§ 9. Задачи для контрольных работ.
Задание 1.
Вычислить определитель третьего порядка:
;
k-номер варианта.
варианта.
Задание 2.
Векторы
и
образуют угол
.
Найти длину вектора
,
если
.
к- номер варианта.
Задание 3.
Коллинеарны ли
векторы
и
,
если
k-номер варианта.
Задание 4.
Даны вершины
треугольника
.
Найти площадь треугольника АВС.
k- номер варианта.
Задание 5.
Компланарны ли векторы
.
k-номер варианта.
Задание 6.
Вычислить объем пирамиды с вершинами в точках A,B,C,D и длину высоты, опущенной из вершины D.
1.
.
2.
.
3.
.
4.
.
5.
.
6.
.
7.
.
8.
.
9.
.
10.
.