Свойства скалярного произведения.
Скалярное произведение двух векторов обладает переместительным свойством:
.
Скалярное произведение обладает распределительным свойством и сочетательным свойством относительно скалярного множителя:
,
.
Пример 1.
Найти угол между векторами
и
.
Решение.
.
Пример 2.
Определить, при каком
вектор
перпендикулярен вектору
.
Решение.
Пример 3.
Вычислить проекцию вектора
на вектор
,
если
и
.
Решение.
Упражнения.
1.Векторы
и
образуют угол
;
зная, что
.
Вычислить
: 1)
;
2)
;
3)
;
4)
;
5)
; 6)
.
2.Даны
векторы
.
Вычислить: 1)
;
2)
;
3)
;
4)
;
5)
;
6)
.
3.
Вычислить косинус угла, образованного
векторами
и
.
4. Даны
вершины треугольника
и
.
Определить его внутренний угол при вершине А.
5. Вектор
,
коллинеарный вектору
,
образует острый угол с осью OZ.
Зная, что
,
найти его координаты.
6.
Вычислить проекцию вектора
на ось вектора
.
7. Даны
две точки
и
.
Вычислить
проекцию вектора
на
ось вектора
.
8.Найти
модуль вектора
,
если
и векторы
образуют друг с другом углы
.
9.При
каких значениях m векторы
и
перпендикулярны?
10. Даны
три последовательные вершины
параллелограмма:
.
Найти его четвертую вершину D
и угол между векторами
и
.
§6 . Векторное произведение векторов.
Векторным
произведением вектора
на вектор
называется вектор обозначаемый символом
и определяемый следующими тремя
условиями:
Модуль вектора
равен
,
где
- угол между векторами
и
,
т.е.
;
вектор перпендикулярен к каждому из векторов
и
;
направление вектора таково, что упорядоченная тройка векторов
является правой (т.е. если «смотреть»
с конца вектора
,
то вращение от
к
по кратчайшему пути совершается против
движения часовой стрелки).
Замечание.
Если один из векторов
и
нулевой, то полагаем
Свойства векторного произведения.
1.
.
2.
.
3.
Если и коллинеарны, то
Геометрический смысл модуля векторного произведения: длина векторного произведения численно равна площади параллелограмма, построенного на векторах и как на сторонах.
Пример 1.
Найти
площадь параллелограмма, построенного
на векторах
и
как на сторонах, если
и угол между векторами
и
равен
.
Решение.
Площадь S искомого параллелограмма равна модулю векторного произведения.
Упражнения.
1. Векторы
и
образуют угол
.
Зная, что
,
вычислить
.
2. Даны
и
.
Вычислить
.
3. Векторы
и
взаимно перпендикулярны. Зная, что
,
вычислить : 1)
;
2)
.
Векторное произведение в координатной форме.
Пусть даны два вектора и .
Векторное произведение равно:
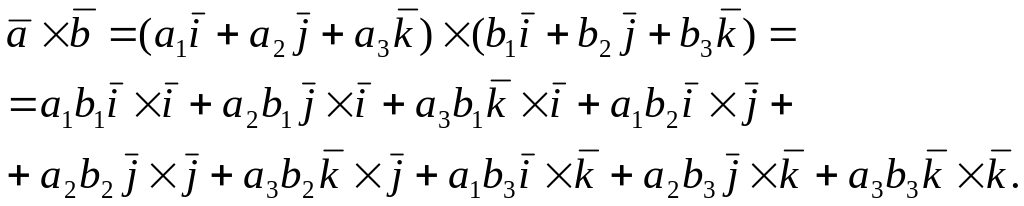
Учитывая
свойство 4,получаем
Тогда
Разности, стоящие в скобках, представляют собой определители второго порядка.
Поэтому
Полученное выражение на основании формулы разложения определителя третьего порядка по элементам первой строки можно символически записать в виде:
.
Следствие. Площадь треугольника, построенного на векторах и как на сторонах, определяется равенством:
.
Пример.
Найти
площадь треугольника, вершины которого
находятся в точках
,
,
.
Решение.
Рассмотрим векторы
и
,
совпадающие со сторонами треугольника:
;
.
Найдем сначала их векторное произведение:
.
.
Упражнения.
1. Даны
векторы
и
.
Найти координаты векторных произведений:
1)
; 2)
; 3)
.
2. Даны
точки
и
.
Вычислить площадь треугольника
.
3.Даны
вершины треугольника
и
.
Вычислить длину его высоты, опущенной
из вершины B на сторону
АС.
4.
Вычислить синус угла, образованного
векторами
и
.
5.
Вычислить площадь параллелограмма,
построенного на векторах
и
.