Методические указания написаны в соответствии с программой курса «Высшая математика».
Рекомендации состоят из 9 параграфов. Сборник содержит варианты контрольных работ, примеры с решениями.
§ 1. Определители второго порядка.
Рассмотрим таблицу вида
, (1)
где
- некоторые числа. Любая такая таблица
называется матрицей второго порядка.
Числа
называются элементами матрицы.
Число,
равное
,
называется определителем матрицы (1)
или определителем второго порядка и
обозначается
.
Итак, по определению = .
Пример 1.
Вычислить
определитель
.
Решение.
.
Пример 2.
Решить
уравнение
.
Решение.
Упражнения.
Вычислить определители:
а)
; б)
; в)
.
Решить уравнения:
а)
; б)
;
в)
.
Свойства определителей второго порядка.
1.Определитель не изменится, если все его строки поменять местами с соответствующими столбцами:
2.При перестановке двух строк (или столбцов) определитель меняет знак:
3.Определитель с двумя одинаковыми строками (столбцами) равен нулю.
4.Общий множитель элементов строки (столбца) можно выносить за знак
определителя:
5.Если к элементам какой-либо строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на один и тот же множитель, то определитель не изменится:
6.Если все элементы какой-либо строки (столбца) равны нулю, то определитель равен нулю.
Все свойства легко доказываются простой проверкой, основанной на правиле вычисления определителей второго порядка.
Докажем, например, свойство 4. Для этого вычислим определитель, стоящий в левой части равенства:
§ 2. Определители третьего порядка.
Рассмотрим квадратную таблицу вида
, (1)
где
- некоторые числа.
Любая такая таблица называется матрицей третьего порядка.
Определитель матрицы (1), или определитель третьего порядка, обозначается
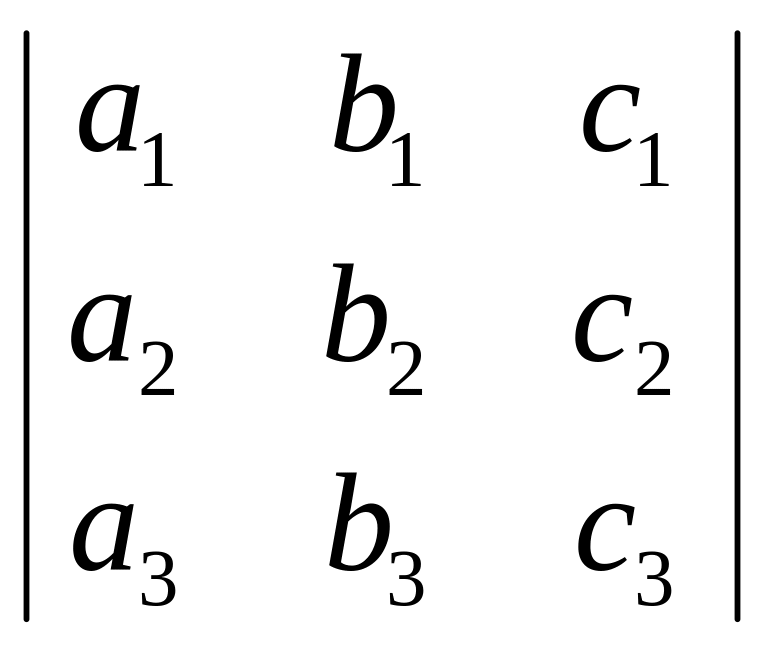
и выражается через определители второго порядка следующим образом:
.
Пример
1. Вычислить определитель
.
Определителем третьего порядка
называется число
Элементы
образуют
главную диагональ, а элементы
-
побочную.
Символически правило вычисления
определителей третьего порядка можно
изобразить следующим образом:
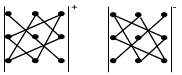
Пример 2. Вычислить определитель:
.
Решение.
Для определителей третьего порядка остаются в силе все свойства определителей второго порядка.
Упражнения.
1.Доказать свойства 1-6 для определителей третьего порядка.
2.Вычислить определители:
1
)
2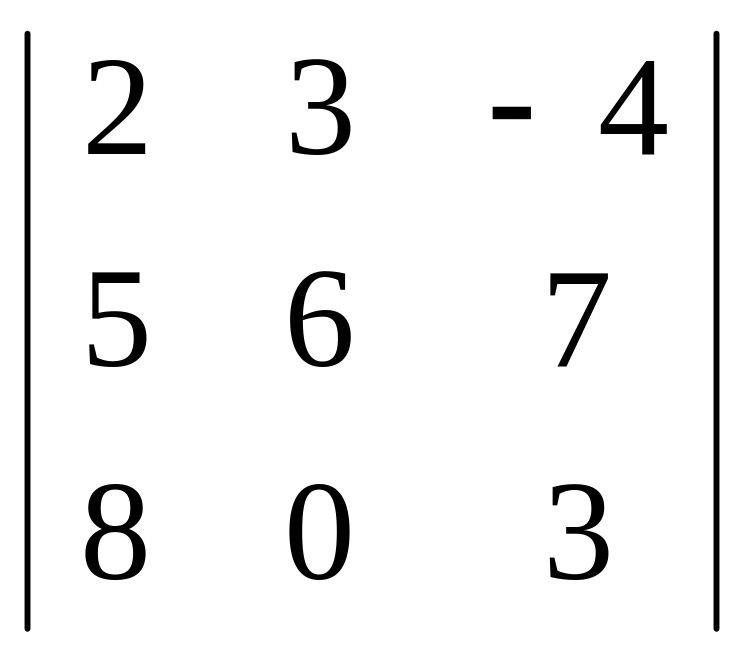
)
3
)
3.Найти
из уравнений :
1
)
2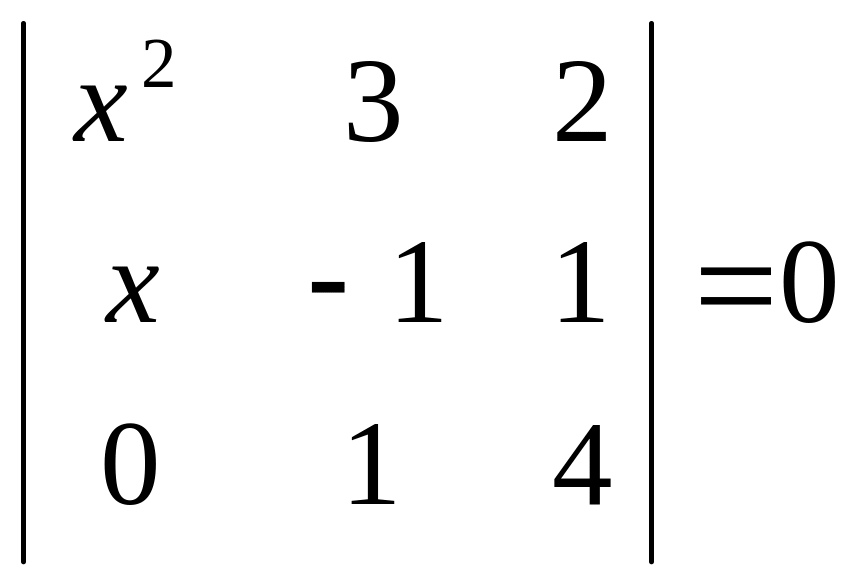
)
§ 3. Понятие вектора. Проекция вектора.
Скалярной называется величина, которая полностью определяется своим числовым значением.
Векторной называется величина, которая, кроме численного значения, характеризуется также направлением в пространстве.
Точка А – начало вектора, точка В – конец.
Вектор обозначаем
или
.
Длиной вектора (модулем)
=
называется число, равное длине отрезка
AB, которое обозначается
.
Если начало и конец вектора совпадают,
то он называется нулевым и обозначается
.
Модуль нулевого векторы равен 0, то есть
.
Два (и
более) вектора
и
называются коллинеарными
,
если они расположены на одной или на
параллельных прямых.
Нулевой вектор коллинеарен любому вектору .
Два вектора называются равными, если они имеют равные модули, коллинеарны и направлены в одну сторону ( = ).
Вектор – равный по модулю и коллинеарный вектору , но направленный в противоположную сторону, называется противоположным вектору .
Если
несколько векторов
,
,…,
параллельны некоторой плоскости, они
называются компланарными.
Если
=1,
то вектор
называется единичным.
Проекцией точки A на ось
u называется точка
,в
которой прямая u пересекается
с прямой, проходящей через A,
перпендикулярной к u.
Проекцией
вектора
на ось
называется вектор
,
где точка
является проекцией на ось
точки
,
а
- проекцией на эту ось точки
.
Проекция
вектора
на
ось
обозначается символом
.
Проекция
вектора
на ось
выражается через его модуль и угол
наклона к оси
формулой:
(1).
Проекции
произвольного вектора
на оси некоторой заданной системы
координат в дальнейшем обозначаются
буквами
.
Равенство
означает, что числа
являются проекциями вектора на
координатные оси.
Проекции
вектора на координатные оси называют
также его координатами. Если даны две
точки
и
,
являющиеся соответственно началом и
концом вектора
,
то его координаты определяются по
формуле:
.
Формула:
(2)
позволяет по координатам вектора определить его модуль.
Если
- углы, которые составляет вектор
с координатными осями, то
называются направляющими косинусами
вектора
.
Вследствие формулы (1)
Отсюда и из формулы (2) следует, что
.
Основные свойства проекций.
1.Равные векторы имеют равные проекции.
2.Проекция суммы векторов равна сумме их проекций.
3.Проекция
произведения вектора
на число равна
произведению числа
на проекцию вектора
Пример 1.
Вычислить
модуль вектора
.
Решение
:
.
Пример 2.
Даны
точки
и
.
Найти
координаты векторов
и
.
Решение :
.
.
Упражнения.
1.Определить
точку
,
с которой совпадает конец вектора
,
если его начало совпадает с точкой
.
2.
Определить начало вектора
,
если его конец совпадает с точкой
.
3.
Вычислить направляющие косинусы вектора
.
4.Может ли проекция ненулевого вектора быть нулевым вектором?
5.Может ли длина проекции вектора быть больше длины этого вектора?