§ 7. Интегрирование рациональных дробей.
Пункт 1. Рассмотрим
интеграл
где
- целый многочлен и а,
в, с –
постоянные
.
Если дробь неправильная, то делим
на
,
получаем в частном некоторый многочлен
и в остатке – линейный двучлен
,
отсюда
.
Пример 1.
Пример 2.
Пример 3.
Пример 4.
Найти интеграл:
.
Решение.
.
Полагаем
,
отсюда
и
.
Следовательно,
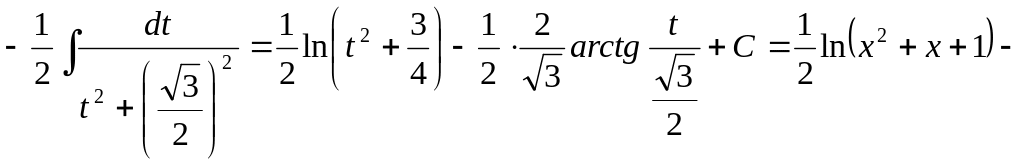
Пример 5.
Найти интеграл
.
Решение. Произведя
деление
на
,
имеем
отсюда
Замечание. Если
квадратный трехчлен
имеет действительные и различные корни
и
,
то для вычисления интеграла можно
воспользоваться разложением подынтегральной
функции на простейшие дроби:
(1)
где А и В – неопределенные коэффициенты. Числа А и В находятся путем приведения равенства (1) к целому виду и приравнивания коэффициентов при одинаковых степенях х в левой и правой частях полученного равенства.
Пример 6.
Найти интеграл
Решение. Приравнивая
знаменатель к нулю, получаем уравнение
;
находим его корни:
и
.
Отсюда, освобождаясь
от знаменателя и учитывая, что
,
получим
,
или
.
Приравнивая друг
к другу коэффициенты при одинаковых
степенях
в правой и в левой частях последнего
равенства, будем иметь
.
Следовательно,
,
.
Получаем
Задачи.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
Если знаменатель
правильной дроби разлагается на множители
вида
и
,
то правильная дробь разлагается на
сумму элементарных дробей следующим
образом:
Пример 7.
Найти интеграл
.
Решение.
Приводя дроби в
правой части к общему знаменателю,
получаем
Сравниваем числители
Раскрывая скобки
в правой части и группируя члены, находим
Сравнивая
коэффициенты при одинаковых степенях
в обеих частях равенства, получим три
уравнения для определения неизвестных
коэффициентов
,
,
:
Решая эту систему,
находим:
,
,
.
Следовательно,
и поэтому
Задачи. Найти интегралы:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
§ 8. Интегрирование тригонометрических функций.
1. Интегралы вида
,
,
находятся с помощью тригонометрических
формул:
2. Интегралы вида
где
и
- четные числа, находятся с помощью
формул:
Если хотя бы одно
из чисел
или
- нечетное, то интеграл находим
непосредственно, отделяя от нечетной
степени один множитель и вводя новую
переменную. В частности, если
,то
3. Интегралы вида
где R
– рациональная
функция от
и
,
приводятся к интегралам от рациональных
функций новой переменной с помощью
подстановки
,
при этом
,
,
.
Доказательство. Имеем:
т.е.
Далее,
т.е.
Наконец,из равенства
имеем:
Таким образом ,
Подынтегральная функция рациональна относительно t.
Пример 1.
Найти интеграл
Решение.
Полагаем
Тогда
Если
,
то целесообразно применить подстановку
,
при этом
,
,
,
.
Пример 2.
Найти интеграл
Решение.
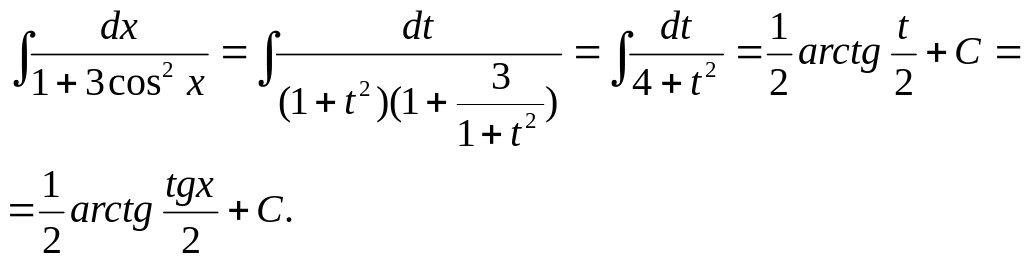
Пример 3.
Найти интеграл
Решение.
Пример 4.
Найти интеграл
Решение.
Задачи. Найти интегралы:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
Вариант 1.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 2.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 3.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 4.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 5.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 6.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 7.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 8.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 9.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 10.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 11.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 12.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 13.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 14.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 15.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 16.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 17.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 18.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 19.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 20.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 21.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
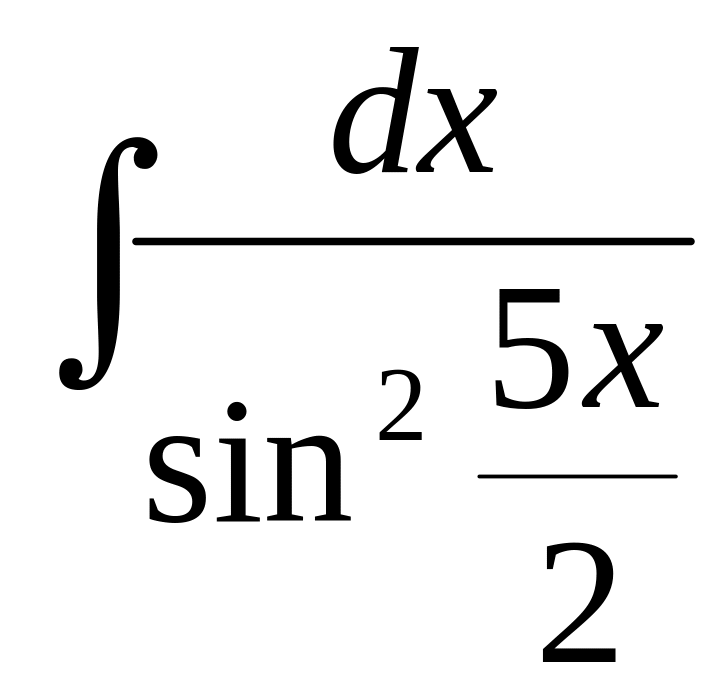
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 22.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 23.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 24.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
Вариант 25.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.