3.Основная формула электронографии

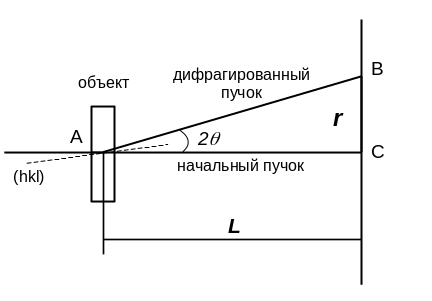
На рис 2 представлена схема дифракции в приборе (электронографе или электронном микроскопе, когда он работает в режиме электронографа) «а» и в обратной решетке «б».

а б

Рис.2.

L – расстояние от объекта до фотопластины.

r – расстояние на фотопластине от следа начального пучка до дифрагированного.

(hkl) – индексы отражающей плоскости.

 - угол Вульфа – Брэгга.

H_hkl - вектор обратной решетки.

Сферу отражения заменяют плоскостью, треугольники ABC и ODE подобны, отсюда:

Из последней записи видно, что электронограмма представляет сечение обратной решетки, проходящее через начальный узел (000), в масштабе L.

Используя свойство вектора обратной решетки

,

где d_hkl – межплоскостное расстояние можно записать:

- Основная формула электронографии.

(На практике удобно измерять 2r, поэтому вводят множитель 2).

2L является константой прибора при данной величине ускоряющего потенциала. Поскольку длина волны в электронографии строго не определена (зависит от ускоряющего потенциала, его стабилизации), то в случае точных измерений 2L вычисляется для каждой электронограммы. Это возможно благодаря использованию эталонного вещества с известным набором межплоскостных расстояний d_hkl. В качестве эталонов будут использоваться вещества: NaCl, MgO, NH₄Cl.

На фото 1 приведена электронограмма эталона NaCl, а таблице 2 – значения межплоскостных расстояний для применяемых эталонов.

Фото 1. Электронограмма от эталона NaCl.

Таблица 2.

Значение индексов интерференции и межплоскостные расстояния для используемых эталонов

NaCl		MgO		NH4Cl
hkl	dhkl (Å)	hkl	dhkl (Å)	hkl	dhkl (Å)
111 200 220 311 222 400 331 420 422	3,25 2,815 1,99 1,695 1,626 1,408 1,29 1,26 1,15	111 200 220 311 222 400 331 420 422 511, 333 440	2,42 2,10 1,485 1,266 1,213 1,05 0,963 0,940 0,937 0,860 0,854	100 110 111 200 210 211 220 300 310 311 222	3,85 2,72 2,22 1,92 1,72 1,57 1,37 1,288 1,221 1,165 1,115

4.Типы электронограмм

В зависимости от характера съемки различают два вида электронограмм – электронограммы на прохождение – когда используемый объект просвечивается электронным лучом и электронограммы на отражение – когда электронный луч почти скользит вдоль исследуемой поверхности образца. В том и другом случае в отражающее положение попадают атомные плоскости почти параллельные падающему пучку электронов.

Различают следующие типы электронограмм.

1. Электронограммы поликристалла – концентрические кольца получаются от беспорядочно расположенных на подложке кристалликов (фото 2).

Фото 2. Электронограмма поликристалла.

2. Точечные электронограммы с рефлексами в виде пятен. Получаются от монокристаллов или монокристаллических сростков (мозаика) с угловым разбросом блоков порядка 2 – 3^о (фото 3).

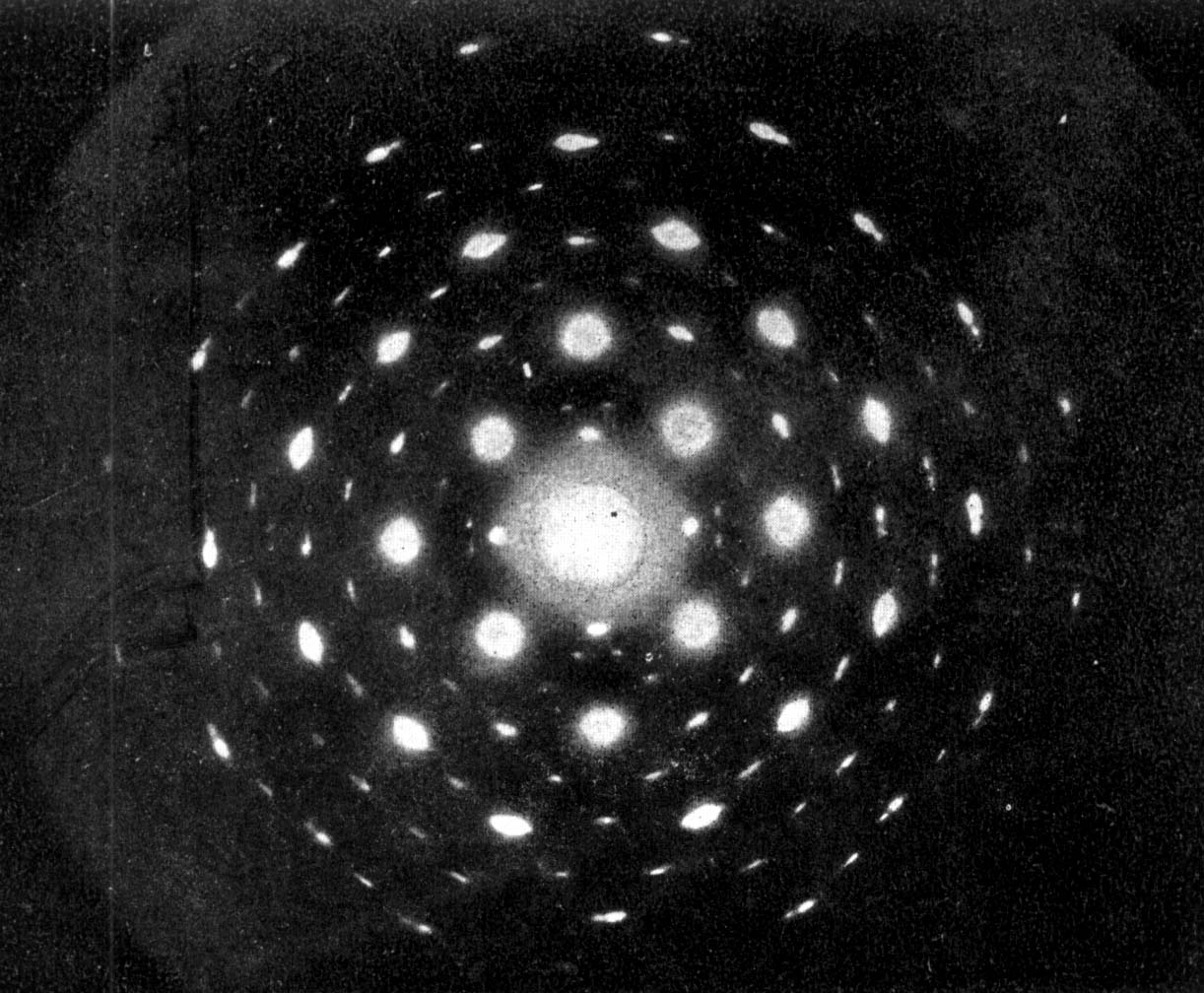
Фото 3. Электронограмма от мозаичного монокристалла.

3. Электронограммы от текстур с рефлексами в виде колец или дуг получаются от закономерно ориентированных на подложке кристалликов, у которых определенная грань параллельна подложке, но сами они беспорядочно распределены по азимуту (фото 4).

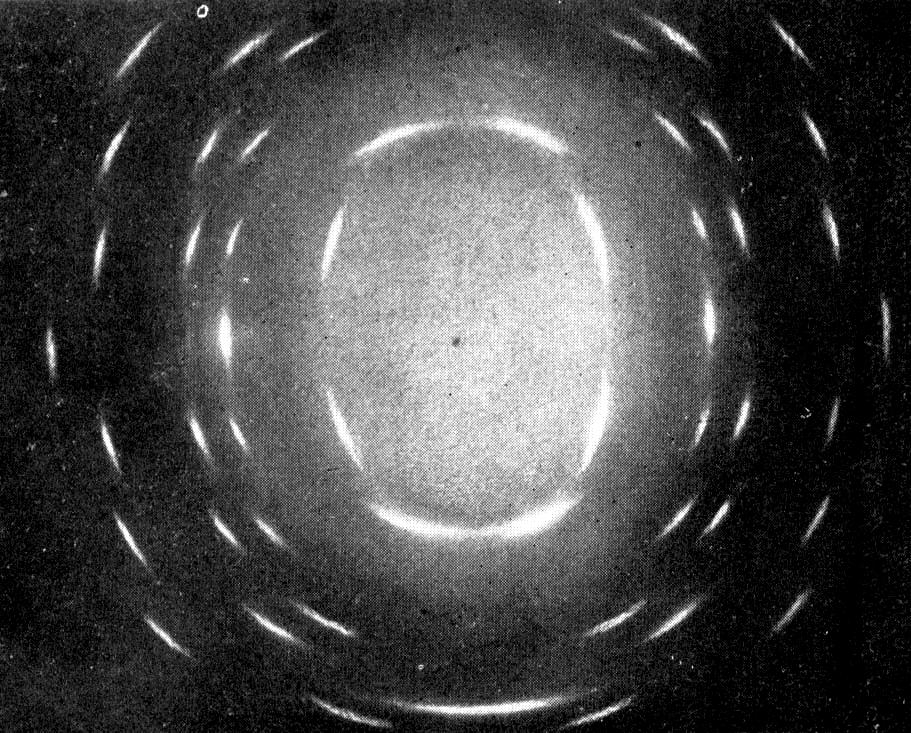
Фото 4. Электронограмма от текстуры.

4. Электронограммы с Кикучи – линиями получаются от совершенных монокристаллов с большим размером блоков и малой разориентацией (фото 5).

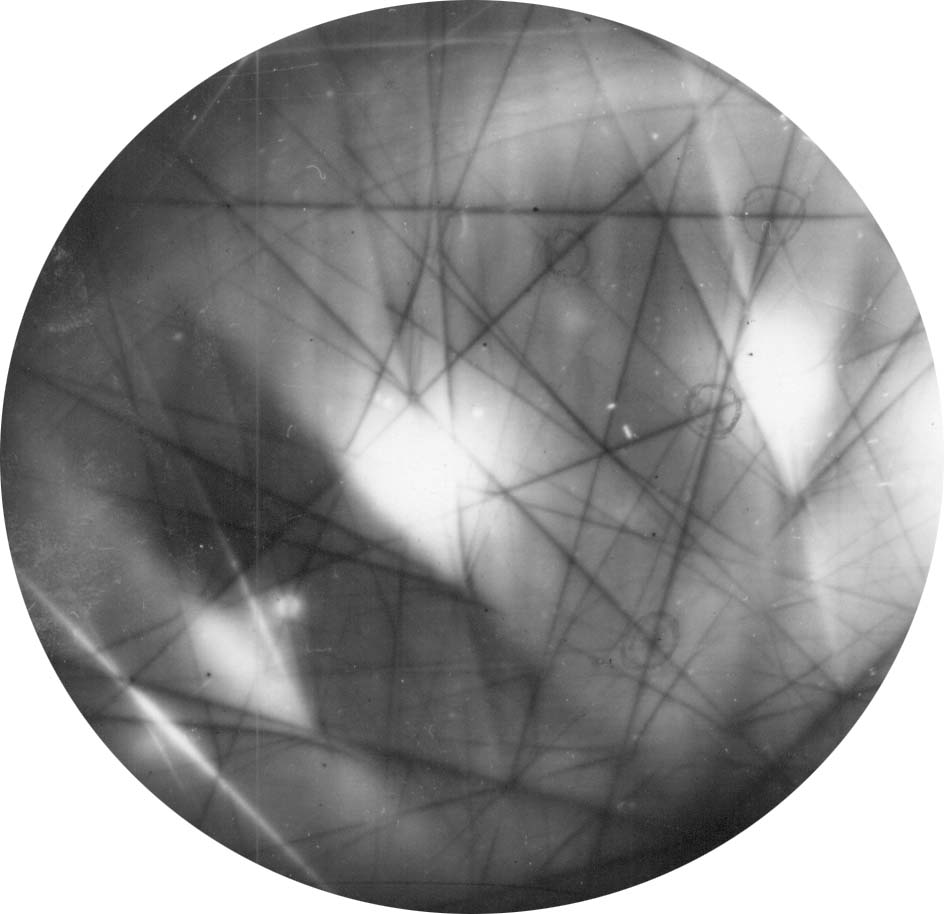
Фото 5. Электронограммы с Кикучи линиями.

Часто получаются электронограммы, являющиеся комбинацией выше перечисленных. Рассмотрим основные типы электронограмм, их геометрию, пользуясь понятием обратной решетки и определением электронограммы.