9) Математическое моделирование и алгоритм расчета процесса многокомпонентной ректификации на произвольной тарелке ректификационной колонны с учетом массопредачи.
Схематическое изображение потоков на тарелке ректификационной колонны:
Для построения компьютерной модели процесса принимаются следующие допущения:
процесс протекает в стационарном режиме,
движение потока жидкости может быть представлено моделью идеального смешения, а пара – идеального вытеснения,
на тарелке протекает многокомпонентная массопередача,
перекрестными эффектами матрицы коэффициентов массопередачи можно пренебречь,
потоки жидкости и пара на тарелке постоянны.
i = 1, …, N
j = 1, …, n
Для многокомпонентных балансов потока жидкости:
j = 1, …, n
j = 1, …, n
- выражение для определения локальных скоростей массопередачи
(L) – верхний индекс, позволяющий отнести переменную к жидкой фазе
M-
матрица коэффициентов массопередачи
FМ – площадь поверхности массопередачи
(s
= 1, …, n)
– равновесный состав жидкости
Концентрация жидкости (мольная доля) не изменяется.
Для покомпонентных балансов потока пара (идеального вытеснения):
j = 1, …, n
(V) – верхний индекс, позволяющий отнести переменную к паровой фазе
n – текущая координата высоты парожидкостного слоя на тарелке колонны
В процессе ректификации при переносе частиц компонентов потока из жидкой фазы в паровую будет справедливо:
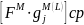определяется
как:
j = 1, …, n
Уравнение покомпонентного баланса:
j = 1, …, n
Уравнение локальной скорости многокомпонентной массопередачи для паровой фазы в математической форме:
* - равновесный
состав паровой фазы
Недиагональные элементы матрицы коэффициентов массопередачи называются ее перекрестными эффектами, и они на 2-3 порядка меньше диагональных элементов, поэтому ими пренебрегают.
Матрица коэффициентов массопредачи становится диагональной:
Следовательно,
j = 1, …, n
Система уравнений, описывающая многокомпонентной массопередачи на тарелке, может быть представлена в виде системы трех уравнений:
j
= 1, …, n
j =
1, …, n
j
= 1, …, n
После подстановки третьего выражения системы во второе получим:
j = 1, …, n
j =
1, …, n
Аналитическое решение дифференциальных уравнений системы дает:
Эффективность
тарелки выражается:
Т. О. эффективность тарелки по каждому компоненту может быть определена:
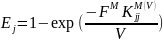j
= 1, …, n
Состав паровой фазы, покидающей тарелку:
j
= 1, …, n
Для теоритической
тарелки, где устанавливается
термодинамическое равновесие жидкость
– пар:
,
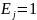Уравнение баланса для жидкой фазы:
j = 1, …, n
Уравнение баланса для паровой фазы:
j
= 1, …, n
Уравнение для эффективности тарелки по компоненту:
j
= 1, …, n
Уравнение для равновесного состава паровой фазы:
Константа фазового равновесия:
j =
1, …, n
(
)
Давление насыщенного пара индивидуального вещества определяется по уравнению Антуана:
Система обычно дополняется стехиометрическими соотношениями для составов фаз, выраженных в долях.