1.2.5. Обработка экспертных оценок, полученных по методу ранжирования

Оценками объектов эксперта i являются ранги объектов .

Анализ оценок каждого эксперта

В методе ранжирования проверка экспертных оценок производится на выполнение следующих условий:

а) все ранги должны быть либо целыми числами, либо кратными 1/2;

б) , (23)

В случае если для оценок какого-либо эксперта эти условия не вы­полняются, производится коррекция рангов аналитиком или программой обработки данных.

Определение групповых оценок объектов

Групповой ранг ( ) объекта j определяется как медиана распределения рангов , присвоенных этому объекту всеми экспертами. Для этого ранги упорядочиваются по воз­растанию и групповой оценкой является среднее по порядку полученного ряда. Например, оценками объекта j являются следующие ранги:

Э¹ Э² Э³ Э⁴ Э⁵

O_j 1 3 2 3 3

После упорядочения получим ряд: 1; 2; 3; 3; 3. Групповой оценкой r_j объекта j будет 3.

Вычисленные групповые оценки r_j еще не будут групповыми ран­гами, так как не всегда выполняется условие (23), определяющее правиль­ность вычисления связанных рангов. Поэтому по ряду r_j необ­ходимо определить групповые ранги объектов . Если, например, , то .

В случае, когда заданы коэффициенты компетентности экспертов , медиана распределения определяется из условия равенства суммы kⁱ слева и справа от r_j. Для этого вычисляется , упорядоченному ряду рангов сопоставляется ряд коэффициентов компетентности экспертов, и находится r_j, соответствующий K_m. Так, если в рассматриваемом выше примере заданы коэффициенты компетентности экспертов , то упо­рядоченному ряду рангов соответствует ряд коэффи­циентов компетентности , а .

Вычисленному K_m по ряду Kⁱ соответствует оценка эксперта с коэф­фициентом компетентности равным 6, т.е. оценка второго эксперта в упо­рядоченном ряду. Значит, r_j = 2 является групповой оценкой объекта.

Анализ достоверности групповых оценок

В методе ранжирования оценку достоверности можно проводить, используя коэффициент согласия или устойчивость групповых оценок.

Оценка согласованности экспертов. Рассмотрим сначала вопрос оценки согласованности двух экспертов i и l. Для сравнения оценок, полученных по методу ранжирования, можно использовать коэффициенты ранговой корреляции по Спирмену и по Кендэлу [6]. Более надежным из них является коэффициент ранговой корреляции по Спирмену, который в дальнейшем и будет использоваться:

. (24)

Получим выражение для Sⁱ и .

. (25)

Среднее значение рангов

(26)

тогда для случая, когда в оценках эксперта нет связанных рангов, выраже­ние (25) будет иметь вид:

.

Учитывая, что , выражение для перепишется в виде:

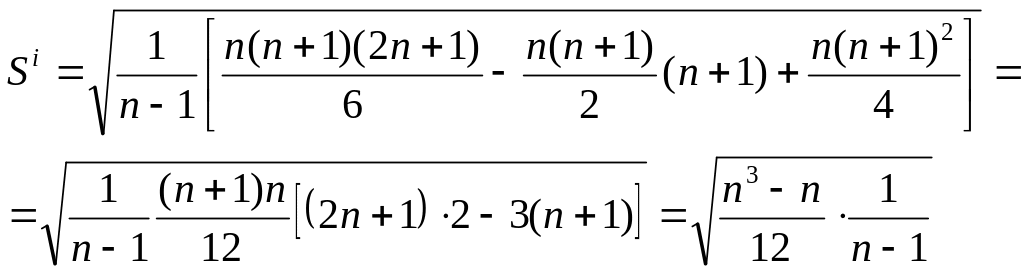(27)

При наличии t связанных ранггов у эксперта значение суммы в выражении (27) уменьшится на

.

Если в оценках эксперта i имеется несколько групп связанных рангов, то уменьшению будет соответствовать

,

где n_i – число различных рангов, присвоенных экспертом i объектам (очевидно, что n_i<n, а при отсутствии связанных рангов n_{i =} n ); – число повторений j ранга в оценках i эксперта.

Обозначим через .

Таким образом, при наличии связанных рангов Sⁱ будет определяться выражением:

. (28)

Следует отметить, что при отсутствии связанных рангов (все и ) и выражение (28) совпадает с (27), значит (28) является общим для вычисления Sⁱ.

Получим выражение для :

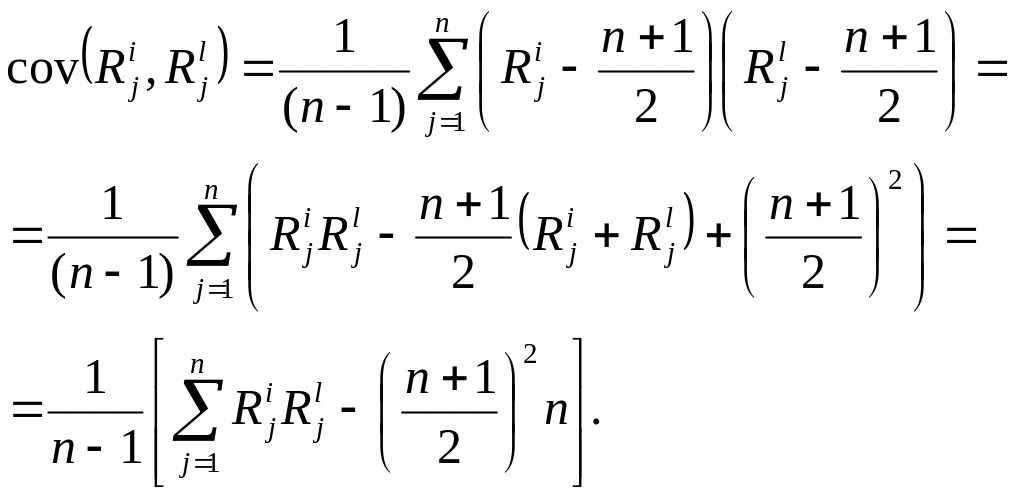(29)

К правой части выражения (29) прибавим и вычтем 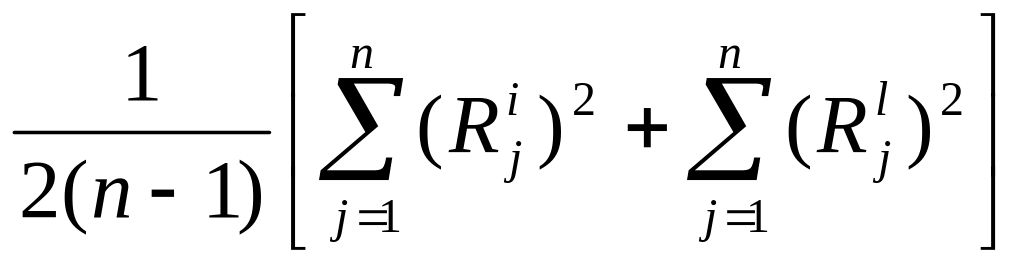, после чего получим:

.

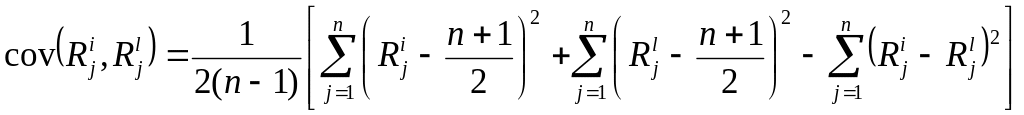Обозначим через , тогда с учетом (26) и (27) последнее выражение примет вид:

. (30)

Если в оценках i или l экспертов присутствуют связанные ранги, то уменьшается на или .

Тогда выражение для ковариации будет иметь вид

. (31)

С учетом (31) и (28) общее выражение для коэффициента корреляции запишется в виде:

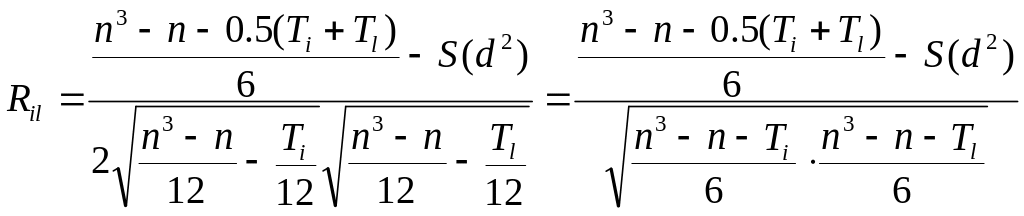. (32)

Преобразуем знаменатель R_il:

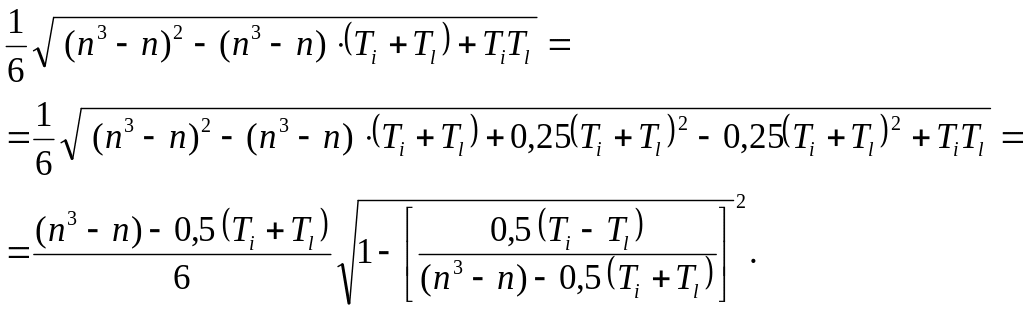
Если много меньше , то тогда

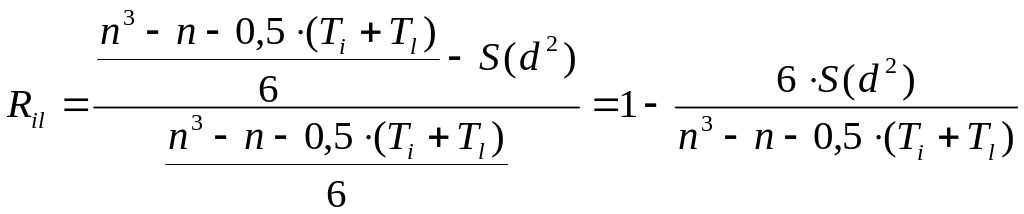. (33)

Если же T_i = T_l = 0 то

. (34)

Для проверки значимости , т.е. проверки гипотезы о независимости оценок i и l экспертов, используем в качестве статистики . При небольшом числе объектов (n < 10) для проверки значимости используются таблицы распределения , приведенные в приложении 1.

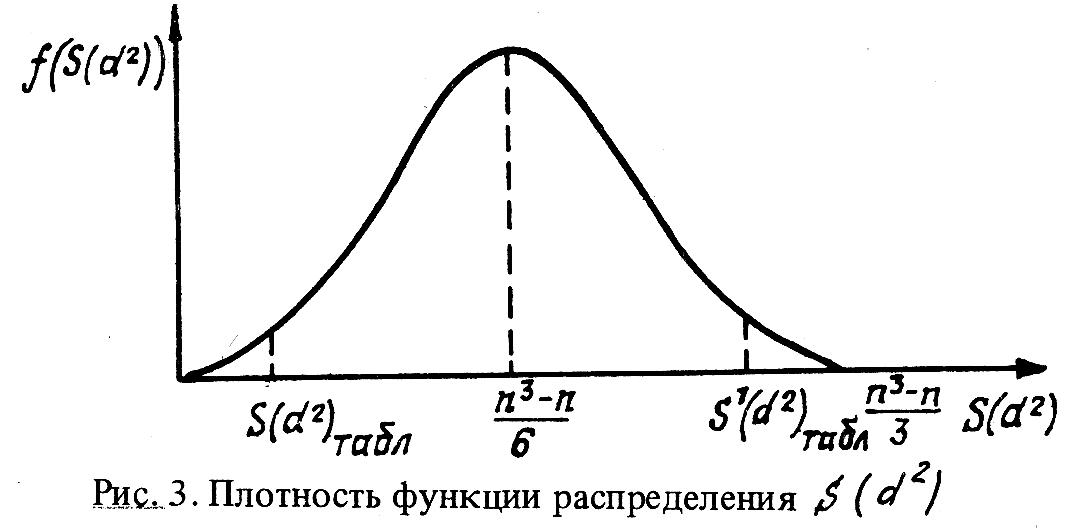
Распределение симметрично (см. рис. 3), соответствует , тогда из (34) и (33) следует, что = . Среднее значение равно .

Задав уровень значимости для проверки гипотезы H₀, по таблице находится α-квантиль (если альтернативная гипотеза заключается в положительной связи) или – (если альтернативная гипотеза H₁ заключается в отрицательной связи).

Решающим правилом для отвержения гипотезы является или

или (35)

Перепишем выражение (24) для в виде

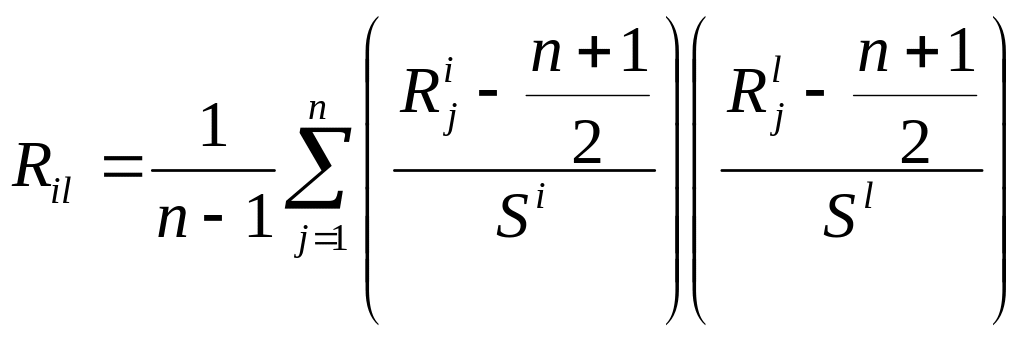. (36)

В соответствии с выдвинутой гипотезой, и независимы, поэтому:

, а . (37)

При достаточно большом числе слагаемых в (36) (n ), в соответствии с центральной предельной теоремой, распределено по нормальному закону. Учитывая первые два момента (37), получаем, что

– (38)

нормально распределенная величина с параметрами N(0;1).

Поэтому при ( ) для проверки значимости коэффициента ранговой корреляции по заданному уровню значимости определяется . Решающее правило для того, чтобы считать коэффициент значимым, имеет вид .

Коэффициент ранговой корреляции используется для оценки связи рангов каждого эксперта с групповыми рангами объектов.

Получим выражение для коэффициента согласия всех экспертов E:

.

Для случая отсутствия связанных рангов в оценках экспертов с учетом (26) и (27) выражение для E перепишется в виде:

.

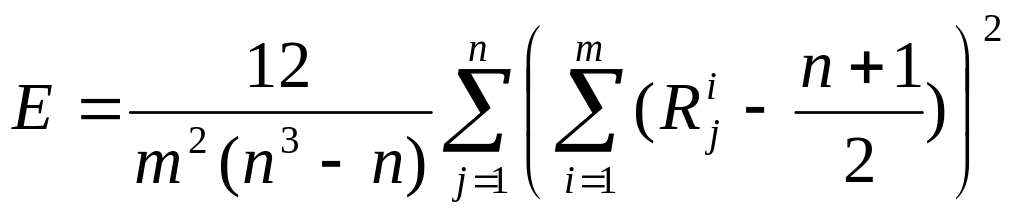Обозначив через , запишем формулу для вычисления коэффициента согласия в виде:

, (39)

где . (40)

Если в оценках всех экспертов присутствуют связанные ранги и T_i одинаковы, то с учетом (28):

.

Если же T_i отличаются друг от друга незначительно, то приближенная формула для E записывается в виде:

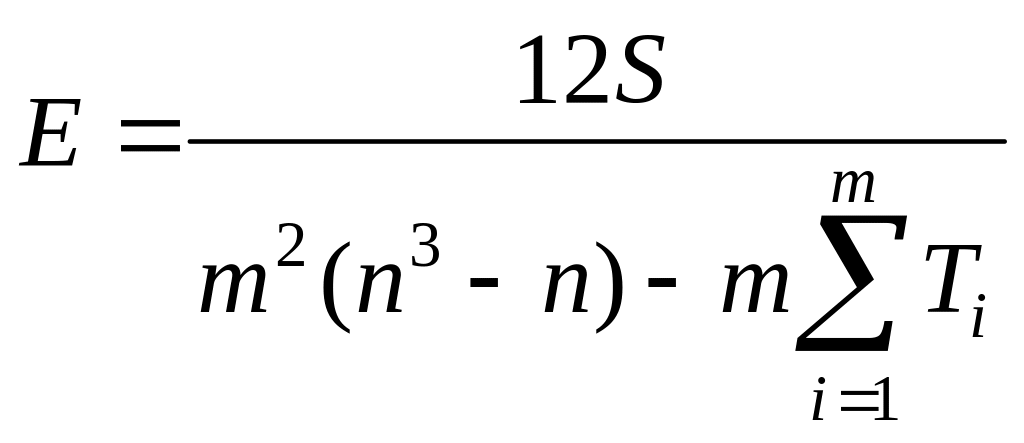. (41)

Выражение (41) обычно и используется при ручном расчете коэффициента согласия.

При малых значениях m и n для проверки значимости коэффициента согласия используются специальные таблицы (см. приложение 2), в которых в качестве статистики выступает величина S, вычисляемая по формуле (40).

При m(n-1 )> 20 и m < 7 для проверки значимости коэффициента согласия используется распределение Фишера:

, (51)

.

при числе степеней свободы

При достаточно большом числе экспертов распределение E стремится к распределению 2 (Пирсона). Покажем это.

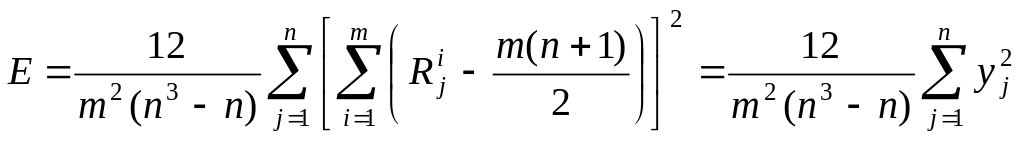, (54)

где .

При достаточно большом m y_j распределено по нормальному закону. Параметры нормального распределения с учетом (27) и (27) будут равны: 

.

Пронормируем y_j в соответствии с выражением:

.

Тогда (54) перепишется в виде , где u_j нормально распределена с и .

Как указывалось в п.5, сумма квадратов независимых нормально распределенных случайных величин распределена по закону 2 с числом степеней свободы .

Получили, что если гипотеза о независимости оценок экспертов (m>7) верна, то статистика

(55)

распределена по закону Пирсона с числом степеней свободы  = n-1. Таким образом, в зависимости от количества экспертов т, числа оцениваемых объектов n, для проверки значимости Е необходимо вос­пользоваться или таблицами распределения S (когда т(п-1)  20 ), или распределением Фишера ( , а т  7 ), или -распределени­ем (т > 7).

В соответствии с заданным уровнем значимости гипотезы о неза­висимости оценок экспертов α находятся или S_табл, или F_табл или _2табл.

Решающими правилами для того, чтобы считать коэффициент согла­сия значимым, т.е. чтобы считать групповые оценки достоверными, являют­ся:

S_расч > S_табл ; F_расч > F_табл ; _2расч > _2табл.

Следует подчеркнуть, что при расчете по формулам (53) числа степеней свободы для F-распределения ₁ и ₂ их следует округлять в большую сторону.