Алгоритм нахождения левого разбора по таблице разбора

Вход: 1. КС-грамматика в нормальной форме Хомского без пустых правил (ВСЕХ!!!) и входная цепочка . Предполагается, что правила из занумерованы числами .

2. Таблица разбора , построенная для цепочки .

Выход: Левый разбор цепочки или сигнал – «ошибка».

Метод:

Опишем рекурсивную процедуру , порождающую левый разбор, соответствующий выводу .

1. Делаем проверку: если , то и переходим к шагу 2, в противном случае, если , выдаем сигнал – «ошибка».

2. Вызываем процедуры . перед вызовом процедуры положим .

3. Если и правило 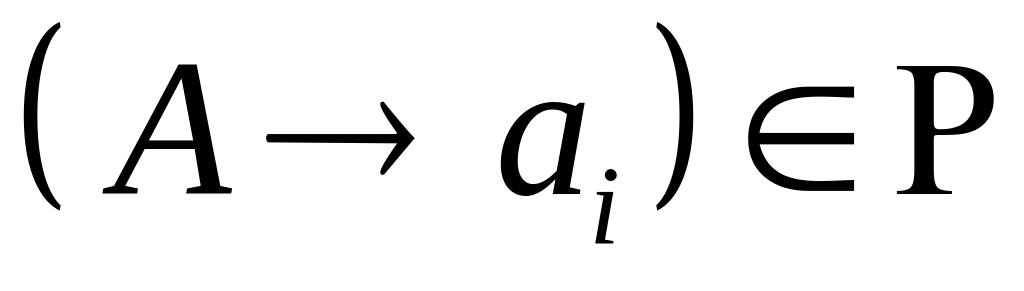имеет номер , то .

4. Пусть и . Пусть это правило имеет номер (если правил несколько, то возьмем любое, например, с наименьшим номером). Тогда выдать номер , т.е. и выполнить , а затем .

Пример №1

Задание.

Пусть задана грамматика в нормальной форме Хомского с правилами

и пусть - входная цепочка. Также задана таблица разбора вида

	1	2	3	4	5
1
2
3
4
`5

Решение.

Пронумеруем правила.

Выполним первый шаг алгоритма. Делаем проверку. Так как , то переходим ко второму шагу алгоритма.

На втором шаге назначаем и вызываем процедуру .

, .

: ,

: ,

: ,

: ,

: ,

: ,

: ,

: ,

Домашнее задание: При определении начать рассмотрение с максимального номера.

Домашнее задание: При выборе номера правила из нескольких выбирают максимальный.

Алгоритм Эрли

Алгоритм работает следующим образом. Пусть – КС-грамматика и - входная цепочка. Объект вида назовем ситуацией к цепочке , если - правило из и . Точка « » между и является метасимволом, для которого имеет место условие . Число может быть любым целым числом от нуля (в этом случае точка – первый символ) до (в этом случае она последний символ. Примечание. Если правило имеет вид , то ситуация будет такой: ).

Для каждого построим такой список ситуаций , что тогда и только тогда, когда для некоторых и существуют выводы и . Таким образом, между второй компонентой ситуации и номером списка, где она появляется, заключена часть входной цепочки, выводимая из . Другие условия, налагаемые на ситуацию, просто гарантируют возможность применения правила в выводе некоторой входной цепочки, совпадающей с до позиции .

Последовательность списков будем называть списком разбора для входной цепочки . Заметим, что принадлежит тогда и только тогда, когда в есть ситуация вида .