2.2.2. Дискретні марковські процеси, їх характеристики

Під системою розуміють множину взаємозв’язаних елементів, які не можна розчленити на незалежні підмножини. Якщо система змінює з часом свій стан випадковим чином, то говорять, що в системі протікає випадковий процес. Нехай – можливі стани системи , причому у будь-який момент часу система знаходиться в одному з них, тобто .

Якщо множина станів скінчена, то говорять, що вона дискретна, інакше – неперервна. Якщо система має дискретну множину станів, то вона переходить зі стану в стан стрибком, якщо ж система має неперервну множину станів – то плавно.

Випадковий процес, що протікає в системі , називається марковським, якщо йому властива відсутність післядії (тобто для кожного моменту часу ймовірність будь-якого стану системи в майбутньому (при ) залежить від її стану в сьогоденні (при ) і не залежить від того, як і скільки часу розвивався цей процес у минулому.

Для аналізу дискретного випадкового процесу зручно користуватися графами станів системи. Під графом станів системи розуміють множину вузлів, що позначають стани системи, і множину гілок можливих безпосередніх переходів зі стану в стан. При вивченні системи слід з’ясувати, в яких станах вона може знаходитися, які переходи зі стану в стан можливі й побудувати граф станів.

Дискретні марковські процеси можуть бути з дискретним та неперервним часом.

Випадковий процес, що протікає у системі називається процесом з дискретним часом, якщо переходи системи зі стану в стан можуть здійснюватися тільки в наперед визначені моменти часу , які називаються кроками (етапами) цього процесу.

Випадковий процес, що протікає у системі, називається процесом з неперервним часом, якщо переходи системи зі стан в стан можливі у будь-які випадкові моменти часу.

Основною характеристикою марковських ланцюгів є ймовірності станів системи на -му кроці, тобто ймовірності того, що система від -го до -го кроку перебуватиме у стані .

Для кожного кроку події несумісні й утворюють повну групу подій, отже,

(2.11)

Перехідними ймовірностями з -го в -й стан системи для -го кроку називаються ймовірності безпосереднього переходу системи у момент часу зі стану в стан . Якщо , то перехідна ймовірність називається ймовірністю затримки системи в стані . Якщо перехідні ймовірності не залежать від номеру кроку , марковський процес називається однорідним і перехідні ймовірності позначаються замість . Якщо ж хоч би одна ймовірність змінюється з номером кроку , то марковський ланцюг називається неоднорідний. Перехідну ймовірність марковського ланцюга записують у вигляді квадратної матриці -го порядку

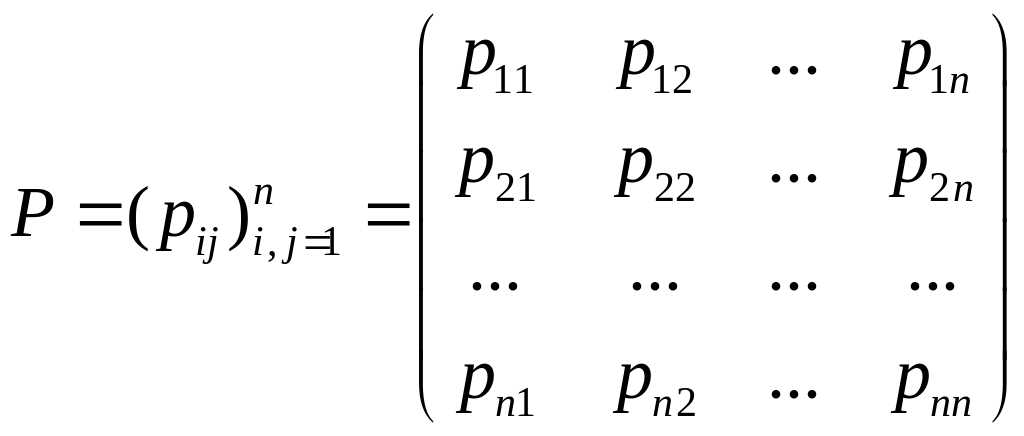. (2.12)

Перехідні ймовірності інтерпретують як умовні ймовірності

(2.13)

подій (з -го до -го кроку система знаходиться в стані ) за умови, що мали місце події .

Враховуючи, що події несумісні й утворюють повну групу подій, матимемо

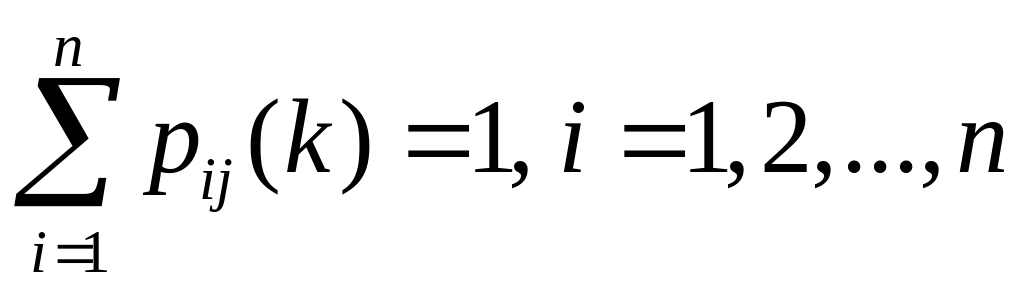(2.14)

Тобто сума елементів кожного рядка матриці перехідних ймовірностей дорівнює 1.

На практиці часто зустрічаються випадкові процеси, в яких система змінює свої стани в будь-який випадковий момент часу  випадкові процеси з неперервним часом.

Нехай  можливі стани системи . Тоді ймовірністю -го стану системи в момент часу називається ймовірність

(2.15)

події , яка полягає у тому, що система у момент часу знаходиться у стані . Марковський дискретний процес з неперервним часом вважається вивченим, якщо знайдені ймовірності всіх станів .

Але ймовірності переходу у випадку процесу з неперервним станом вже не грають тієї визначальної ролі в обчисленні ймовірностей станів, яку вони виконували у випадку процесу з дискретним часом. Замість перехідних імовірностей у процесі з неперервним часом розглядають інші характеристики процесу  так звані щільності ймовірностей переходу зі стану в стан .

Щільністю ймовірностей переходу системи зі стану в стан у момент часу називається величина

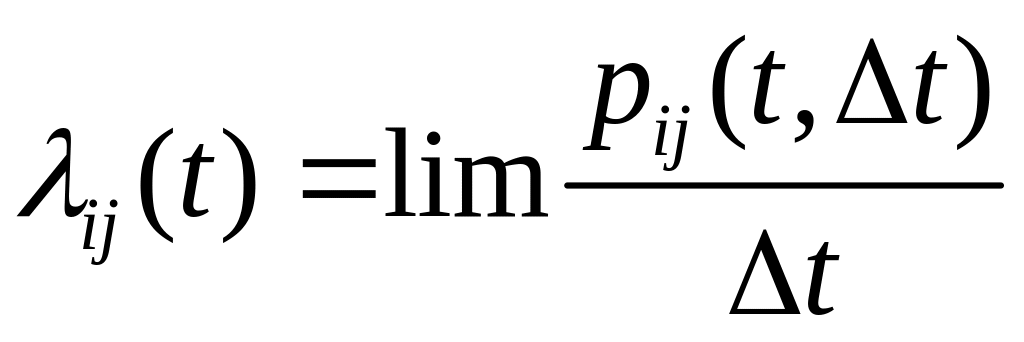. (2.16)

З визначення щільності ймовірностей випливає, що

. (2.17)

Якщо при будь-якому , щільності ймовірностей переходів не залежать від (тоді замість писатимемо просто , марковський процес з неперервним часом називається однорідним.

Якщо ж хоч би при одній парі значень щільність ймовірностей переходів змінюється з часом , то процес називається неоднорідним.

Розглянемо далі однорідний дискретний марковський процес з неперервним часом.

Граф станів марковського однорідного процесу з неперервним часом, у гілок якого вказані щільності ймовірностей переходів, називається розміченим.

Знаючи щільності ймовірностей переходів, можна скласти систему диференціальних рівнянь, щодо ймовірностей станів , а саме, справедлива наступна теорема.

Ймовірність станів (невідомі ймовірнісні функції) є розв’язком наступної системи диференціальних рівнянь:

. (2.18)

Дану теорему довів відомий радянський математик Колмогоров А.М. (1093  1987). Саме він заклав основи теорії марковських випадкових процесів з неперервним часом і отримана ним система називається системою диференціальних рівнянь Колмогорова.

Оскільки шукані функції  функції однієї змінної, а саме, часу , то кожне рівняння є звичайним диференціальним рівнянням. Оскільки невідомі функції та їх похідні входять в рівняння тільки в першому ступені, то кожне рівняння системи називають лінійним.

Оскільки найвищий порядок похідних і шуканих функцій  перший, то рівняння системи є диференціальними першого порядку. Оскільки в кожному рівнянні системи вільні члени дорівнюють 0, то рівняння системи є однорідними. Нарешті, оскільки розглядаємо однорідний процес, то коефіцієнти в рівняннях постійні (щодо часу ).

Отже, система (2.18) є системою звичайних однорідних диференціальних рівнянь першого порядку з постійними коефіцієнтами.

Скласти систему диференціальних рівнянь Колмогорова зручно по одному з наступних правил.

1) Правило складання диференціальних рівнянь Колмогорова за розміченим графом станів.

Для того, щоб скласти диференціальне рівняння Колмогорова для функцій , треба у лівій частині цього рівняння записати похідну функції , а в правій  добуток суми щільності ймовірностей переходів для гілок, що виходять зі стану на ймовірність цього стану зі знаком мінус, плюс суму 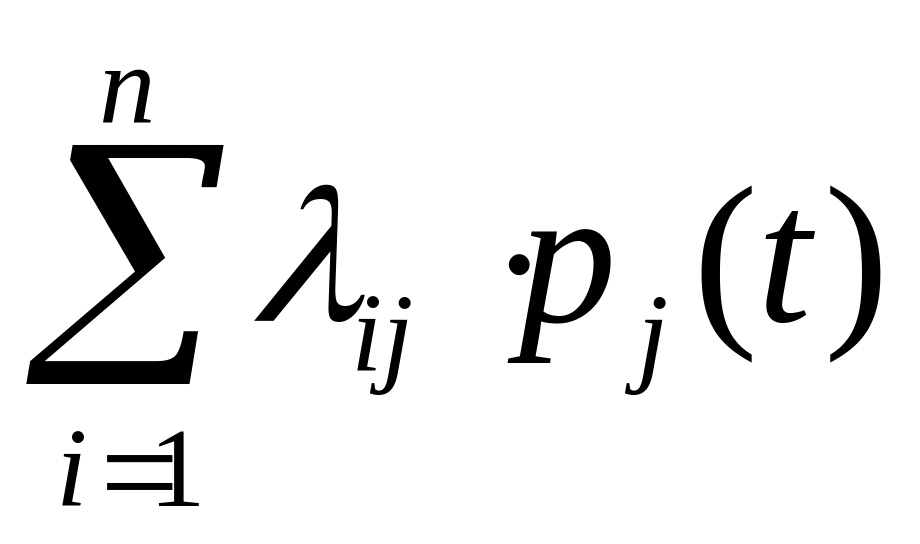, що входять до стану та ймовірностей станів , з яких ці гілки виходять. При цьому щільності ймовірностей переходів , відповідні відсутнім на графі гілкам, дорівнюють нулю.

2) Правило складання диференціальних рівнянь Колмогорова за матрицею щільності ймовірності переходів.

Щоб скласти диференціальне рівняння Колмогорова для функції треба в лівій частині цього рівняння записати похідну функції , а в правій  добуток суми елементів -го рядка матриці та ймовірності стану (номер якого співпадає з номером обраного рядка) за знаком мінус, плюс суму добутків елементів -го стовпця та відповідної ймовірності .

Початкові умови системи диференціальних рівнянь Колмогорова визначаються заданим розподілом ймовірностей станів системи в початкові моменти часу : і задовольняють умовам нормування

(2.19)

Якщо в початкові моменти часу система знаходиться в стані , то з урахуванням умови нормування отримуємо початковий розподіл ймовірностей

. (2.20)

Система диференціальних рівнянь 1-го порядку, розв’язаних щодо похідних шуканих функцій, які входять до неї, називається системою, що має нормальну форму Коші.