2.3.2. Системи масового обслуговування з очікуванням. Одноканальна смо з очікуванням

Найпростіша з усіх можливих СМО з очікуванням – одноканальна система (n – 1), на яку надходить потік заявок з інтенсивністю , інтенсивність обслуговування заявок позначимо через . Заявка, що надходить у момент, коли канал зайнятий, стає у чергу та очікує обслуговування.

Система з обмеженою довжиною черги. Припустимо спочатку, що кількість місць у черзі обмежене числом m, тобто якщо заявка прийшла в момент, коли в черзі вже знаходиться m – заявок, вона залишає систему не обслуженою. Надалі, спрямувавши m до нескінченності, ми одержимо характеристики одноканальної СМО без обмежень довжини черги.

Будемо нумерувати стани СМО по числу заявок, що перебувають у системі, що як обслуговуються, так і очікують обслуговування:

– канал вільний;

– канал зайнятий, черги немає;

– канал зайнятий, одна заявка стоїть в черзі;

– канал зайнятий, k-1 заявок стоять у черзі;

– канал зайнятий, m - заявок стоять у черзі.

Графова модель системи зображена на рисунку 2.6. Усі інтенсивності потоків подій, що переводять у системі по стрілках з ліва на право, рівні , а справа наліво – . Дійсно, по стрілках з ліва на право систему переводить потік заявок (як тільки прийде заявка, система переходить у наступний стан), а справа наліво – потік «звільнень» зайнятого каналу, що має інтенсивність (як тільки буде обслугована чергова заявка, канал або звільниться, або зменшується число заявок у черзі).

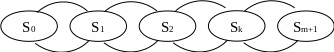
Рисунок 2.6 – Одноканальна СМО з очікуванням

З схеми яка зображена на рисунку 2.6 можна записати наступний вираз для граничних імовірностей станів:

(2.44)

або з використанням

(2.45)

Останній рядок у (2.45) містить геометричну прогресію з першим членом 1 і знаменником , звідки одержуємо:

(2.46)

тому граничні ймовірності має вид:

(2.47)

Вираз (2.46) дійсний тільки при (при воно дає невизначеність типу ). Сума геометричної прогресії із знаменником дорівнює , тоді .

Визначимо характеристики СМО: імовірність відмови , відносну пропускну здатність , абсолютну пропускну здатність А, середню довжину черги , середнє число заявок, пов’язаних із системою , середній час очікування в черги, середній час перебування заявки в СМО .

Імовірність відмови. Очевидно, заявка одержує відмову тільки у випадку, коли канал зайнятий і всі m- місць у черзі теж.

. (2.48)

Відносна пропускна здатність

. (2.49)

Абсолютна пропускна здатність

. (2.50)

Середня довжина черги. Знайдемо середнє число – заявок, що перебувають у черзі, як математичне очікування дискретної випадкової величини R – числа заявок, що перебувають у черзі .

З імовірністю в черзі стоїть одна заявка, з імовірністю – дві заявки, взагалі на загал з імовірністю в черзі стоять заявок, і т.д., звідки

. (2.51)

Оскільки , суму в (2.51) можливо пояснити як похідну по від суми геометричної прогресії

.

Підставляючи даний вираз в (2.49) і використовуючи з (2.47), маємо

. (2.52)

Середнє число заявок, що перебувають у системі. Одержимо далі формулу для середнього числа - заявок, пов’язаних із системою (як стоячих у черзі, що так і перебувають на обслуговуванні). Оскільки , де – середнє число заявок, що перебувають під обслуговуванням, а відомо, то залишається визначити . Оскільки канал один, число заявок, що обслуговуються, може рівнятися 0 (з імовірністю ) або 1 (з імовірністю ), звідки:

. (2.53)

Середнє число заявок, пов’язаних з СМО, дорівнює

. (2.54)

Середній час очікування заявки в черзі. Позначимо його . Якщо заявка проходить у систему в якийсь момент часу, то з імовірністю канал обслуговування не буде зайнятий, і їй не доведеться стояти в черзі (час очікування дорівнює нулю). З імовірністю вона прийде в систему під час обслуговування якоїсь заявки, але перед нею не буде черги, і заявка буде чекати початку свого обслуговування протягом часу (середній час обслуговування однієї заявки). З імовірністю в черзі перед розглянутою заявкою буде стояти ще одна, і час очікування в середньому буде дорівнювати , та ін.

Якщо ж , тобто коли знову заявка, що приходить застає канал обслуговування зайнятим і - заявок у черзі (імовірність цього ), то в цьому випадку заявка не стає в чергу (і не обслуговується), тому час очікування дорівнює нулю.

Середній час очікування буде дорівнювати:

,

якщо підставити сюди вираз для ймовірності (2.47), отримаємо:

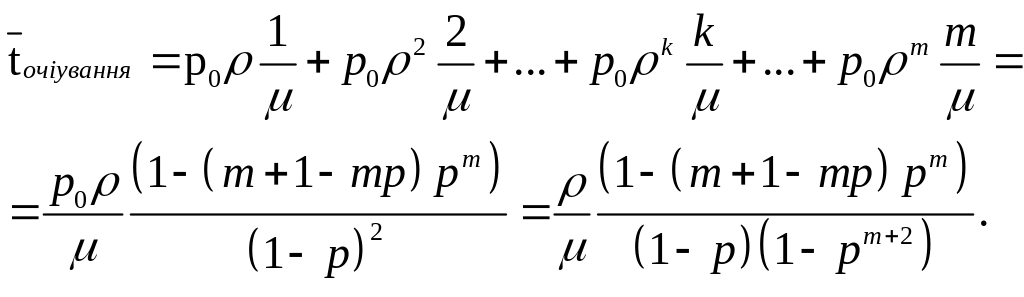(2.55)

Тут використані співвідношення (2.51), (2.52) (похідна геометричної прогресії), а також із (2.4). порівнюючи цей вираз з (2.52), зауважимо, що інакше кажучи, середній час очікування дорівнює середньому числу заявок у черзі, поділеному на інтенсивність потоку заявок

. (2.56)

Середній час перебування заявки в системі. Позначимо – математичне сподівання випадкової величини – час перебування заявки в СМО, яке складається із середнього часу очікування в черзі ( ) й середнього часу обслуговування . Якщо завантаження системи становить 100%, очевидно, , в іншому ж випадку . Звідси

. (2.57)