4. Определение натуральной величины отрезка способом прямоугольного треугольника.

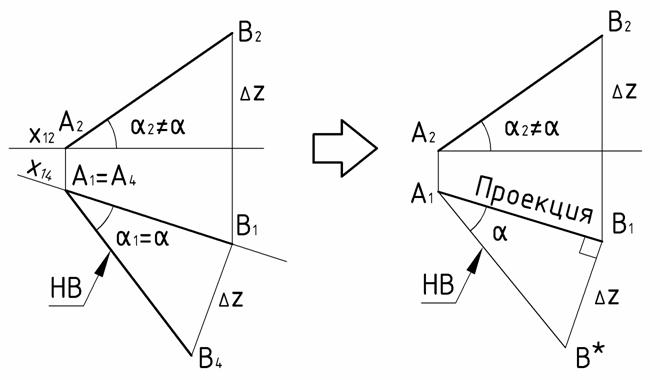
Способ прямоугольного треугольника. Способ прямоугольного треугольника применяется в задачах, в которых требуется определить натуральную величину отрезка, разность координат концов отрезка, углы наклона его к плоскостям проекций и так далее. Посмотрим на способ прямоугольного треугольника как частный случай замены плоскостей проекций. Это тот случай определения длины отрезка, когда один из его концов принадлежит плоскости проекций, а новая плоскость проекций проводится через сам отрезок (Рис.58). На чертеже это новая ось, совпадающая с проекцией отрезка. При этом искомая величина отрезка окажется равной гипотенузе прямоугольного треугольника, один из катетов которого есть проекция отрезка. Помимо длины треугольник содержит в себе и другие сведения об отрезке.Точно такой же треугольник с точно такими же сведениями об отрезке можно получить без операции проецирования и даже – на безосном комплексном чертеже. Применим одну из проекций отрезка за катет прямоугольного треугольника. Второй катет равен разности координат концов отрезка в направлении, в каком была задана выбранная проекция.

1) Длина отрезка равна гипотенузе прямоугольного треугольника, один катет которого – это проекция отрезка, второй катет – равен разности координат концов отрезка, измеренной в направлении получения использованной проекции отрезка.

2) Угол наклона отрезка к плоскости проекций равен углу между гипотенузой и проекцией отрезка на той же плоскости.

Пример (Рис.59). Определить длину отрезка и угол его наклона  к плоскости .

При определении длины отрезка за катет прямоугольного треугольника может быть выбрана любая проекция отрезка. Другое дело, если определяется угол наклона отрезка к той или иной плоскости проекций. Здесь выбор падает на проекцию отрезка, принадлежащую именно той же плоскости проекций.

Решение:

Строим прямоугольный треугольник, приняв за катет фронтальную проекцию отрезка . Второй катет по длине равен разности координат точек  и  в направлении мнимой в данном случае оси y. На чертеже эта разница берется на другой плоскости проекций: на плоскости . Из построенного треугольника делаем выводы:

1) ,

2) .

Выносной элемент - дополнительное отдельное изображение (обычно увеличенное) какой-либо части предмета, требующей пояснений в отношении формы, размеров и иных данных. Геликоид - линейчатая поверхность, образованная при винтовом движении прямолинейной образующей.

5. Взаимное положение прямых в пространстве. Конкурирующие точки. Определение видимости на эпюре.

В разделе прямая на плоскости мы дали представление о точке и прямой на плоскости. Прямую линию в пространстве следует представлять абсолютно аналогично: мысленно отмечаем две точки в пространстве и проводим с помощью линейки линию от одной точки до другой и за пределы точек в бесконечность.

Все обозначения точек, прямых и отрезков в пространстве аналогичны случаю на плоскости.

Вообще, прямая линия целиком принадлежит некоторой плоскости в пространстве. Это утверждение вытекает из аксиом:

• через две точки проходит единственная прямая;

• если две точки прямой лежат в некоторой плоскости, то все точки прямой лежат в этой плоскости.

Существует еще одна аксиома, которая позволяет рассматривать прямую в пространстве как пересечение двух плоскостей: если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

Перейдем к вариантам взаимного расположения двух прямых в пространстве.

Во-первых, две прямые могут совпадать, то есть, иметь бесконечно много общих точек (по крайней мере две общие точки).

Во-вторых, две прямые в пространстве могут пересекаться, то есть, иметь одну общую точку. В этом случае эти две прямые лежат в некоторой плоскости трехмерного пространства. Если две прямые в пространстве пересекаются, то мы приходим к понятию угла между пересекающимися прямыми.

В-третьих, две прямые в пространстве могут быть параллельными. В этом случае они лежат в одной плоскости и не имеют общих точек. Рекомендуем к изучению статью параллельные прямые, параллельность прямых.

После того как мы дали определение параллельных прямых в пространстве, следует сказать о направляющих векторах прямой линии в силу их важности. Любой ненулевой вектор, лежащий на этой прямой или на прямой, которая параллельна данной, будем называть направляющим вектором прямой. Направляющий вектор прямой очень часто используется при решении задач, связанных с прямой линией в пространстве.

Наконец, две прямые в трехмерном пространстве могут быть скрещивающимися. Две прямые в пространстве называются скрещивающимися, если они не лежат в одной плоскости. Такое взаимное расположение двух прямых в пространстве приводит нас к понятию угла между скрещивающимися прямыми.

Особое практическое значение имеет случай, когда угол между пересекающимися или скрещивающимися прямыми в трехмерном пространстве равен девяноста градусам. Такие прямые называют перпендикулярными (смотрите статью перпендикулярные прямые, перпендикулярность прямых).

Конкурирующие точки. Две точки в пространстве могут быть расположены по-разному. В отдельном случае они могут быть расположены так, что проекции их на какой-нибудь плоскости проекций совпадают. Такие точки называются конкурирующими. На рис. 64, а приведен комплексный чертеж точек А и В. Они расположены так, что проекции их совпадают на плоскости П₁ [А₁ == В₁]. Такие точки называются горизонтально конкурирующими. Если проекции точек A и В совпадают на плоскости

Рис. 64

П₂(рис. 64, б), они называются фронтально конкурирующими. И если проекции точек А и В совпадают на плоскости П₃ [А₃ == B₃] (рис. 64, в), они называются профильно конкурирующими. По конкурирующим точкам определяют видимость на чертеже. У горизонтально конкурирующих точек будет видима та, у которой больше высота, у фронтально конкурирующих — та, у которой больше глубина, и у профильно конкурирующих — та, у которой больше широта.