8.5. Оценка достоверности выборочных показателей
Чтобы по данным какой-либо выборки можно было судить о всей генеральной совокупности, следует учитывать величины, которые в статистике называют ошибками параметров [3, с. 172–176].
Характеристика генеральной совокупности на основе выборочного исследования всегда будет неточной, т. е. будет иметь большую или меньшую ошибку. Такие ошибки являются ошибками обобщения, связанными с перенесением результатов, полученных при изучении выборки, на всю генеральную совокупность. Они определяют меру точности данного параметра.
Среднеарифметическая величина выборки характеризует среднеарифметическую генеральной совокупности лишь приближенно и может отличаться от нее на некоторую величину. Если взять ряд выборок из одной и той же совокупности, то среднеарифметические величины этих выборок не будут совпадать друг с другом. Одни среднеарифметические величины будут несколько больше, другие – несколько меньше. Значения cpедних отдельных выборок будут обладать вариацией, которая может быть измерена среднеквадратическим отклонением. Оно получило название ошибки средней для выборочной средней величины m (x), которая позволяет определить достоверность выборочных показателей и определить, в каких пределах лежат параметры генеральной совокупности. Ошибку средней арифметической величины вычисляют по формуле:
Как видно из формулы, ошибка среднеарифметической величины зависит от численности выборки (числа наблюдений n) и oт большей или меньшей изменчивости признака в выборке, т. е. от среднеквадратического отклонения. Чем меньше изменчивость признака и больше численность выборки, тем точнее будут выборочные данные, меньше будет ошибка среднеарифметической величины и расхождение между значениями признаков в выборочной и генеральной совокупности.
8.6. Корреляция между антропометрическими признаками
Известно, что у людей с одинаковым ростом все другие размерные признаки могут отличаться. Однако между признаками может быть отмечена определенная связь. Так, у людей с большим обхватом груди чаще будут встречаться большие обхваты талии и бедер, чем маленькие. Можно сказать также, что у невысоких людей чаще встречаются меньшие обхваты груди, чем у высоких. Вместе с тем при одном и том же обхвате груди люди могут иметь различную длину тела и в значительной степени варьирующиеся обхваты талии и бедер.
Связь признаков, при которых каждому определенному значению одного признака может соответствовать не одно значение второго признака, а целое распределение этих значений, называется стохастический (корреляционной) связью, или корреляцией [5, с. 185–187].
Причина того, что между антропометрическими признаками существует корреляция, заключается в том, что организм человека развивается под действием очень большого числа факторов, которые по-разному определяют развитие признаков и их связь друг с другом. Корреляция не предполагaeт точную зависимость одного признака от другого, поэтому эта связь может иметь различную степень тесноты. Так, например, очень тесно связаны между собой длиннотные размеры тела, а также обхватные. В качестве примера малой степени тесноты корреляции можно привести зависимость между длиной тела и обхватом груди.
Кроме того, характер корреляции между признаками может быть различным, т. е. с увеличением одного признака другой признак может либо увеличиваться, либо уменьшаться. В первом случае корреляция будет положительной, или прямой, во втором – отрицательной, или обратной.
Большинство антропометрических признаков связано между собой положительной корреляцией. В качестве примера отрицательной корреляции можно привести связь обхватых размеров с глубинами позвоночника. С увеличением обхватов величина некоторых глубин уменьшается.
Статическую величину степени тесноты корреляции между признаками характеризует коэффициент корреляции r.
Формула для вычисления коэффициента корреляции имеет вид:
Как видно из этой формулы, в числителе – сумма произведений отклонений каждого из признаков от своих среднеарифметических величин, а в знаменателе – произведение среднеарифметических отклонений каждого из признаков.
Условно о большой степени тесноты корреляции (связи) можно говорить, если коэффициент корреляции находится в интервале от ±0,750 до ±0,999, о средней связи – от ±0,450 до ±0,749 и о малой – oт 0 до ±0,449. При коэффициенте корреляции, равном нулю, корреляция между признаками отсутствует.
Помимо степени тесноты корреляции и ее направления определяют еще и форму корреляции – прямолинейная и криволинейная.
Прямолинейная корреляция – это такая связь, при которой равномерным изменениям первого признака соответствуют равномерные изменения второго признака. При криволинейной корреляции равномерным изменениям первого признака соответствуют неравномерные изменения второго, причем эта неравномерность имеет определенный закономерный характер (рис. 29, 30).
Степень тесноты корреляции может быть определена не только между двумя признаками, но и одновременно между тремя, четырьмя и т. д. В этом случае применяется коэффициент множественной, или совокупной, корреляции.
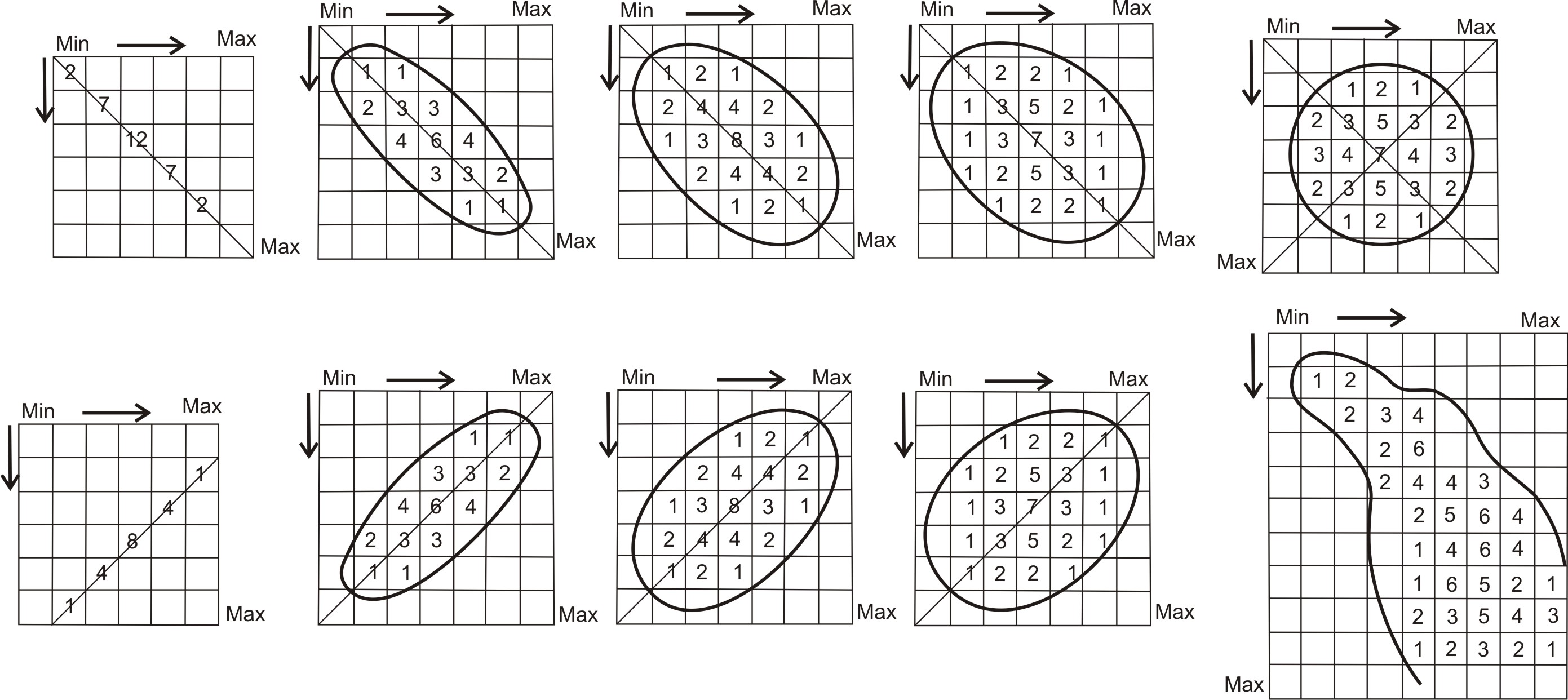
rxy = +1,0 rxy = +0,75 rxy = +0,50 rxy = +0,25
а
rxy = –1,0 rxy = –0,75 rxy = –0,50 rxy = –0,25
б
rxy = 0,0
в
Рис. 29. Схема степеней прямолинейно корреляции: а – при прямой корреляции;
б – при обратной; в – при ее отсутствии
Рис. 30. Схема корреляционного поля при криволинейной связи