Прототип b11 № 318146

В правильной четырёхугольной пирамиде с основанием боковое ребро равно 5, сторона основания равна . Найдите объём пирамиды.

Решeние:

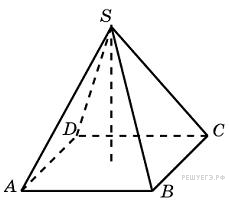В основании правильной четырехугольной пирамиды лежит квадрат, вершина пирамиды проецируется в его центр. Введем обозначения, как показано на рисунке. Диагонали квадрата перпендикулярны друг другу, треугольник прямоугольный и равнобедренный. В нем

Тогда из прямоугольного треугольника находим, что

Откуда для объема пирамиды имеем:

Ответ: 24.

Прототип b11 № 245344

Найдите объем многогранника, вершинами которого являются точки правильной шестиугольной призмы , площадь основания которой равна 6, а боковое ребро равно 3.

Решeние:

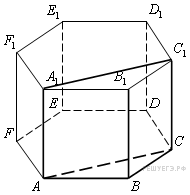Многогранник, объем которого требуется найти, является прямой треугольной призмой. Объем призмы равен произведению площади основания на высоту. Основанием призмы является треугольник, его площадь равна одной шестой площади основания шестиугольной призмы. Высотой прямой призмы является боковое ребро, его длина равна 3. Таким образом, искомый объем равен 3.

Прототип b11 № 245349

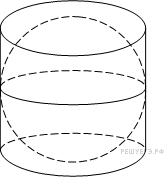Цилиндр описан около шара. Объем шара равен 24. Найдите объем цилиндра.

Решeние:

Объем цилиндра равен произведению площади основания ны высоту. Площадь основания цилиндра равна площади большого круга вписанного шара, а высота цилиндра равна диаметру вписанного шара. Поэтому

Ответ: 36.

Прототип b11 № 27204

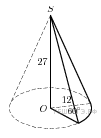Найдите объем части конуса, изображенной на рисунке. В ответе укажите .

Решeние:

Объем данной части конуса равен

.

Ответ: 216.

Прототип b11 № 27215

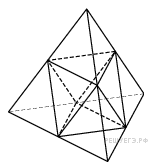Площадь поверхности тетраэдра равна 1,2. Найдите площадь поверхности многогранника, вершинами которого являются середины сторон данного тетраэдра.

Решeние:

Искомая поверхность состоит из 8 равносторонних треугольников со стороной, вдвое меньшей ребра исходного тетраэдра. Поверхность исходного тетраэдра состоит из 16-ти таких треугольников (см. рис.), поэтому искомая площадь равна половине площади поверхности тетраэдра и равна 0,6.

Ответ: 0,6.

Прототип B11 № 27214

Объем тетраэдра равен 1,9. Найдите объем многогранника, вершинами которого являются середины сторон данного тетраэдра.

Решeние:

Объем данного многогранника равен разности объемов исходного тетраэдра и четырех тетраэдров, одни из вершин которых совпадают с вершинами исходного:

.

Ответ: 0,95.

Прототип B11 № 27209

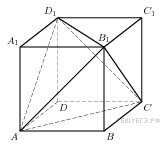Объем параллелепипеда равен 4,5. Найдите объем треугольной пирамиды .

Решeние:

Искомый объем равен разности объемов параллелепипеда со сторонами , и и четырех пирамид, основания которых являются гранями данной треугольной пирамиды:

Ответ: 1,5.

Прототип B11 № 27207

Середина ребра куба со стороной 1,9 является центром шара радиуса 0,95. Найдите площадь части поверхности шара, лежащей внутри куба. В ответе запишите .

Решeние:

Так как середина ребер куба является центром сферы, диаметр которой равен ребру куба, в кубе содержится 1/4 сферы и, соответственно, 1/4 ее поверхности. Имеем:

.

Ответ: 0,9025.

Прототип B11 № 245345

Найдите объем многогранника, вершинами которого являются точки , , , , , , , правильной шестиугольной призмы , площадь основания которой равна 6, а боковое ребро равно 2.

Решeние:

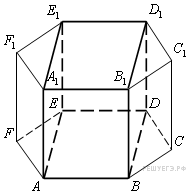Площадь основания четырехугольной призмы равна двум третьим площади основания правильной шестиугольной призмы, а высота у них общая. Поэтому

.

Ответ: 8.

Прототип B11 № 245346

Найдите объем многогранника, вершинами которого являются точки , , , , , , , правильной шестиугольной призмы , площадь основания которой равна 6, а боковое ребро равно 2.

Решeние:

Площадь основания четырехугольной призмы равна половине площади основания правильной шестиугольной призмы, а высота у них общая. Поэтому

.

Ответ: 6.

Прототип B11 № 245348

Цилиндр описан около шара. Объем цилиндра равен 33. Найдите объем шара.

Решeние:

,

Выразим из формулы для объёма цилиндра и подставим в формулу для объёма шара

Ответ: 22.

Прототип B11 № 245347

Найдите объем многогранника, вершинами которого являются точки , , , правильной шестиугольной призмы , площадь основания которой равна 6, а боковое ребро равно 3.

Решeние:

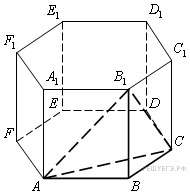Площадь основания треугольной пирамиды равна одной шестой площади основания правильной шестиугольной призмы, а высота у них общая. Поэтому

.

Ответ: 1.

Прототип B11 № 245335

Найдите объем многогранника, вершинами которого являются точки , , , , , прямоугольного параллелепипеда , у которого , , .

Решeние:

Из рисунка видно, что многогранник является половиной данного прямоугольного параллелепипеда. Следовательно, объём искомого многогранника

Ответ: 30.

Прототип B11 № 245336

Найдите объем многогранника, вершинами которого являются точки , , , прямоугольного параллелепипеда , у которого , , .

Решeние:

Площадь основания пирамиды в два раза меньше площади основания пареллелепипеда, а высота у них общая. Поэтому

Ответ: 8.

Прототип B11 № 27114

Объем правильной четырехугольной пирамиды равен 12. Точка – середина ребра . Найдите объем треугольной пирамиды .

Решeние:

Площадь основания пирамиды по условию в 2 раза меньше площади основания пирамиды . Также высота данной треугольной пирамиды в 2 раза меньше высоты пирамиды (т.к. точка – середина ребра ). Поскольку объем пирамиды равен , то объем данной треугольной пирамиды в 4 раза меньше объема пирамиды и равен 3.

Ответ: 3.

Прототип B11 № 27136

Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 3 раза?

Решeние:

Площадь боковой поверхности конуса равна , где – длина окружности основания, а – образующая. При увеличении образующей в 3 раза площадь боковой поверхности конуса увеличится в 3 раза.

Ответ: 3.

Прототип B11 № 27162

Объем одного шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?

Решeние:

Объемы шаров соотносятся как

,

Откуда Площади их поверхностей соотносятся как

.

Ответ: 9.

Прототип B11 № 27139

Диагональ куба равна 1. Найдите площадь его поверхности.

Решeние:

Сторона куба меньше диагонали в раз и равна в данном случае . Тогда площадь поверхности куба

.

Ответ: 2.

Прототип B11 № 27110

Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60 . Высота пирамиды равна 6. Найдите объем пирамиды.

Решeние:

В треугольниках и сторона — общая, и , поэтому эти треугольники равны; треугольник — равносторонний, и . Тогда объем пирамиды

Ответ: 48.

Прототип B11 № 27161

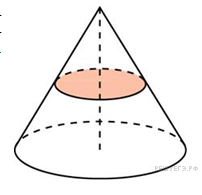Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.

Решeние:

Исходный и отсеченный конус подобны с коэффициентом подобия 2. Площади поверхностей подобных тел относятся как квадрат коэффициента подобия. Поэтому площадь отсеченного конуса в 4 раза меньше площади поверхности исходного. Тем самым, она равна 3.

Ответ: 3.

Прототип B11 № 27157

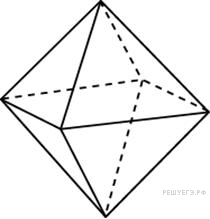Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 3 раза?

Решeние:

При увеличении ребер в 3 раза площади треугольников, образующих грани октаэдра, увеличатся в 9 раз, поэтому суммарная площадь поверхности также увеличится в 9 раз.

Ответ: 9.

Прототип B11 № 27201

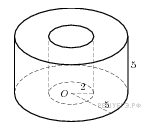Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите .

Решeние:

Объем данной фигуры равен разности объемов цилиндра с радиусом основания 5 и высотой 5 и цилиндра с той же высотой и радиусом основания 2:

.

Ответ: 105.

Прототип B11 № 27196

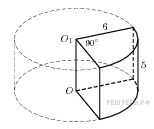Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите  .

Решeние:

Объем данной части цилиндра равен

.

Ответ: 45.

Прототип B11 № 27127

Около куба с ребром  описан шар. Найдите объем этого шара, деленный на .

Решeние:

Пусть длина ребра куба равна а, а его диагональ равна d. Радиус описанного шара R равен половине диагонали куба:

.

Поэтому объем шара равен

Тогда

Ответ: 4,5.

Прототип B11 № 27199

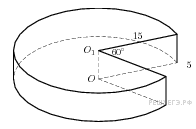Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите  .

Решeние:

Объем данной части цилиндра равен

.

Ответ: 937,5.

Прототип B11 № 27200

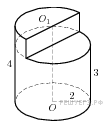Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите .

Решeние:

Объем данной фигуры равен сумме объемов цилиндра с радиусом основания 2 и высотой 3 и половины цилиндра с тем же радиусом основания и высотой 1:

.

Ответ: 14.

Прототип B11 № 27183

Объем куба равен 12. Найдите объем треугольной призмы, отсекаемой от него плоскостью, проходящей через середины двух ребер, выходящих из одной вершины и параллельной третьему ребру, выходящему из этой же вершины.

Решeние:

Поскольку высота куба равна высоте призмы, их объемы пропорциональны площадям их оснований. Площадь основания построенной призмы в 8 раз меньше площади основания исходной, поэтому искомый объем призмы равен 12 : 8 = 1,5.

Ответ: 1,5.

Прототип B11 № 27130

Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в три раза?

Решeние:

Площади подобных тел относятся как квадрат коэффициента подобия, поэтому при увеличении ребра в 3 раза, площадь поверхности увеличится в 9 раз.

Ответ: 9.

Прототип B11 № 27167

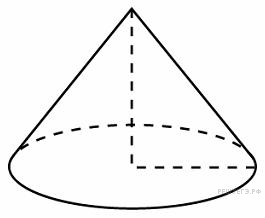Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на .

Решeние:

Найдем образующую по теореме Пифагора: . Площадь полной поверхности конуса

.

Ответ: 24.

Прототип B11 № 27180

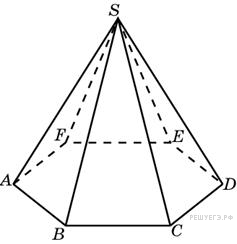Объем правильной шестиугольной пирамиды 6. Сторона основания равна 1. Найдите боковое ребро.

Решeние:

Площадь основания равна

.

Из формулы для объема пирамиды найдем высоту:

.

В правильном шестиугольнике сторона равна радиусу описанной окружности, поэтому найдем боковое ребро пирамиды по теореме Пифагора:

.

Ответ: 7.

Прототип B11 № 27175

Ребра тетраэдра равны 1. Найдите площадь сечения, проходящего через середины четырех его ребер.

Решeние:

Каждая сторона сечения является серединной линией соответствующей грани, которая, как известно, в 2 раза меньше параллельной ей стороны и равна поэтому 0,5. Тогда площадь сечения .

Ответ: 0,25.

Прототип B11 № 27101

Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 3. Объем параллелепипеда равен 36. Найдите его диагональ.

Решeние:

Объем параллелепипеда равен

.

Отсюда найдем третье ребро:

.

Длина диагонали параллелепипеда равна

.

Ответ: 7.

Прототип B11 № 27113

Объем треугольной пирамиды , являющейся частью правильной шестиугольной пирамиды , равен 1. Найдите объем шестиугольной пирамиды.

Решeние:

Данные пирамиды имеют общую высоту, поэтому их объемы соотносятся как площади их оснований. Площадь правильного шестиугольника со стороной равна Площадь же равнобедренного треугольника с боковой стороной и углах при основании равна Получаем, что площадь шестиугольника больше площади треугольника    в   раз и равна 6.

Ответ: 6.

Прототип B11 № 27176

Найдите объем пирамиды, высота которой равна 6, а основание – прямоугольник со сторонами 3 и 4.

Решeние:

Объем пирамиды с площадью основания и высотой равен

.

Ответ: 24.

Прототип B11 № 27122

Конус получается при вращении равнобедренного прямоугольного треугольника вокруг катета, равного 6. Найдите его объем, деленный на .

Решeние:

Треугольник – так же равнобедренный, т.к. углы при основании . Тогда радиус основания равен 6, и объем конуса, деленный на :

Ответ: 72.

Прототип B11 № 27155

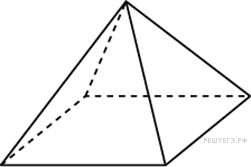Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 и высота равна 4.

Решeние:

Площадь поверхности складывается из площади основания и площади четырех боковых граней: . Апофему найдем по теореме Пифагора: . Тогда площадь поверхности пирамиды:

.

Ответ: 96.

Прототип B11 № 27171

Найдите площадь боковой поверхности правильной четырехугольной пирамиды, сторона основания которой равна 6 и высота равна 4.

Решeние:

Высоту треугольника, образующего грани пирамиды, найдем по теореме Пифагора:

.

Тогда площадь боковой поверхности пирамиды:

.

Ответ: 60.

Прототип B11 № 27125

Радиусы трех шаров равны 6, 8 и 10. Найдите радиус шара, объем которого равен сумме их объемов.

Решeние:

Объем такого шара

,

откуда получим, что .

Ответ: 12.

Прототип B11 № 27159

Высота конуса равна 6, образующая равна 10. Найдите площадь его полной поверхности, деленную на .

Решeние:

Площадь поверхности складывается из площади основания и площади боковой поверхности:

.

Радиус основания найдем по теореме Пифагора для треугольника, образованного высотой, образующей и радиусом: . Тогда площадь поверхности

Ответ: 144.

Прототип B11 № 27104

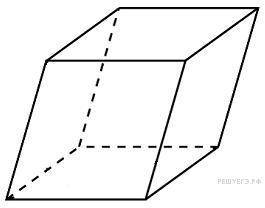Гранью параллелепипеда является ромб со стороной 1 и острым углом 60 . Одно из ребер параллелепипеда составляет с этой гранью угол в 60 и равно 2. Найдите объем параллелепипеда.

Решeние:

Объем параллелепипеда , где – площадь одной из граней, а – длина ребра, составляющего с этой гранью угол . Площадь ромба с острым углом в равна двум площадям равностороннего треугольника. Вычислим объем:

.

Ответ: 1,5.