Прототип B11 № 25561

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решeние:

Площадь поверхности заданного многогранника равна разности площади поверхности прямоугольного параллелепипеда с ребрами 3, 3, 5 и двух площадей квадратов со стороной 1:

.

Ответ: 76.

Прототип B11 № 25581

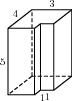Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решeние:

Площадь поверхности заданного многогранника равна разности площади поверхности прямоугольного параллелепипеда с ребрами 3, 4, 5 и площади двух квадратов со стороной 1:

.

Ответ: 92.

Прототип B11 № 25621

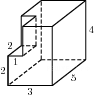Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решeние:

Площадь поверхности заданного многогранника равна площади поверхности прямоугольного параллелепипеда с ребрами 3, 5, 4:

.

Ответ: 94.

Прототип B11 № 25881

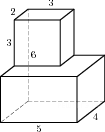Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решeние:

Площадь поверхности заданного многогранника равна сумме площадей параллелепипедов со сторонами 2, 3, 3 и 5, 4, 3 уменьшенной на удвоенную площадь прямоугольника со сторонами 3, 2:

.

Ответ: 124.

Прототип B11 № 27041

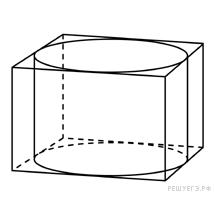Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.

Решeние:

Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому площадь основания равна 4, а объем параллелепипеда равен

.

Ответ: 4.

Прототип b11 № 27042

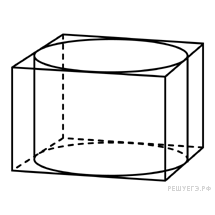Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.

Решeние:

Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому сторона основания равна 8, а площадь основания равна 64. Тогда высота цилиндра равна

Прототип B11 № 27043

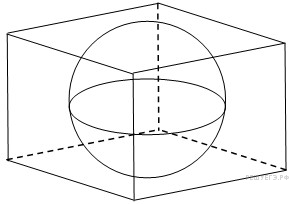В куб вписан шар радиуса 1. Найдите объем куба.

Решeние:

Ребро куба равно диаметру вписанного в него шара, а объем куба равен кубу его ребра. Отсюда имеем:

.

Ответ: 8.

Прототип B11 № 27044

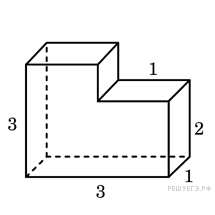Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).

Решeние:

объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).

.

Ответ: 8.

Прототип B11 № 27045

В цилиндрический сосуд налили 2000 воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в .

Решeние:

По закону Архимеда объем детали равен объему вытесненной ею жидкости. Объем вытесненной жидкости равен 9/12 исходного объема:

.

Ответ: 1500.

Прототип B11 № 27046

В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в раза больше первого? Ответ выразите в см.

Решeние:

Объем цилиндрического сосуда выражается через его диаметр и высоту как . При увеличении диаметра сосуда в 2 раза высота равного объема жидкости уменьшится в 4 раза и станет равна 4.

Ответ: 4.

Прототип b11 № 27047

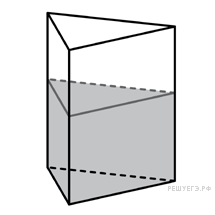Сосуд, имеющий форму правильной треугольной призмы, налили 2300   воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 25 см до отметки 27 см. Найдите объем детали. Ответ выразите в .

Решeние:

По закону Архимеда объем детали равен объему вытесненной ею жидкости. Объем вытесненной жидкости равен 2/25 исходного объема:

Ответ: 184.

Прототип b11 № 27048

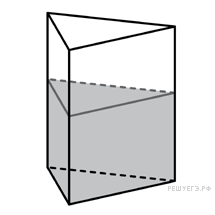В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в см.

Решeние:

Объем сосуда выражается через его высоту и сторону основания как . При увеличении стороны основания в 4 раза уровень воды уменьшится в 16 раз и будет равен 5 см.

Ответ: 5.

Прототип B11 № 27049

В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.

Решeние:

По теореме Пифагора длина гипотенузы треугольника в основании . Поскольку гипотенуза является диаметром основания описанного цилиндра, его объем

.

Ответ: 125.

Прототип B11 № 27050

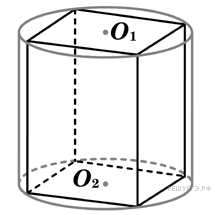В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.

Решeние:

Диагональ квадрата в основании призмы является диаметром описанного вокруг призмы цилиндра. Тогда его объем:

.

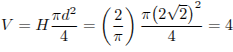Ответ: 4.

Прототип B11 № 27051

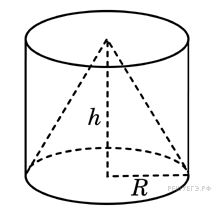Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 25.

Решeние:

Объем цилиндра равен произведению площади основания на высоту, а объем конуса равен одной трети произведения площади основания на высоту. Поскольку они имеют общее основание и высоту, объем цилиндра в три раза больше объема конуса.

Ответ: 75.

Прототип B11 № 27052

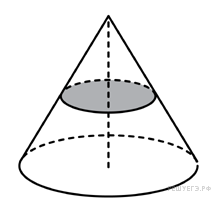Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

Решeние:

Меньший конус подобен большему с коэффициентом 0,5. Объемы подобных тел относятся как куб коэффициента подобия. Поэтому объем меньшего конуса в восемь раз меньше объема большего конуса.

Ответ: 2.