30. Система геодезических координат 1995 года (ск-95)

Единая государственная система геодезических координат 1995 года (СК-95) получена в результате совместного уравнивания трех самостоятельных, но связанных между собой, геодезических построений различных классов точности: КГС, ДГС, АГС по их состоянию на период 1991-93 годов. Объем измерительной астрономо-геодезической информации, обработанной для введения системы координат 1995 года, превышает на порядок соответствующий объем информации, использованной для установления системы координат 1942 года (СК-42).

Космическая геодезическая сеть предназначена для задания геоцентрической системы координат, доплеровская геодезическая сеть – для распространения геоцентрической системы координат, астрономо-геодезическая сеть – для задания системы геодезических координат и доведения системы координат до потребителей.

В совместном уравнивании АГС представлена в виде пространственного построения. Высоты пунктов АГС относительно референц-эллипсоида Красовского определены как сумма их нормальных высот и высот квазигеоида, полученных из астрономо-гравиметрического нивелирования. В процессе нескольких приближений совместного уравнивания высоты квазигеоида для территории отдаленных восточных регионов дополнительно уточнялись с учетом результатов уравнивания. С целью контроля геоцентричности системы координат в совместное уравнивание включены независимо определенные геоцентрические радиус-векторы 35 пунктов КГС и ДГС, удаленных один от другого на расстояния около 1000 км, для которых высоты квазигеоида над общим земным эллипсоидом получены гравиметрическим методом, а нормальные высоты - из нивелирования.

Система координат 1995 года установлена так, что ее оси параллельны осям геоцентрической системы координат. Положение начала СК-95 задано таким образом, что значения координат пункта ГГС Пулково в системах СК-95 и СК-42 совпадают.

Между единой государственной системой геодезических координат 1995 года (СК-95) и единой государственной геоцентрической системой координат «Параметры Земли 1990 года» (ПЗ-90) установлена связь, определяемая параметрами взаимного перехода (элементами ориентирования). Направления координатных осей Z Y X, используемой геоцентрической системы координат определены координатами пунктов КГС; начало координат этой системы установлено под условием совмещения с центром масс Земли.

31 Вынос точек в натуру Способ прямоугольных координат

Способ прямоугольных координат (перпендикуляров) обычно применяют при наличии строительной сетки. В качестве исходных данных для разбивки точки этим способом используются прямоугольные координаты пунктов строительной сетки и точек сооружения. Пусть требуется найти на местности положения точек С и D основной оси сооружения от пунктов 3А4B и 3А5В строительной сетки (рис. 1.20). Координаты точек С и D в системе строительной сетки соответственно , ; , . По координатам пунктов 3А4B и 3А5В и точек С и D вычисляют расстояния , , и : = 425,0 – 400,0 = 25,0 м; = 500,0 – 475,0 = 25,0 м; = 332,5 – 300,0 = 32,5 м; = 332,5 – 300,0 = 32,5 м. От пунктов 3А4B и 3А5В откладывают отрезки и . В полученных точках с помощью теодолита строят прямые углы и по перпендикулярам откладывают отрезки , . Точность отложения углов и линий выбирают по характеристике сооружения (см. табл. 1.2). 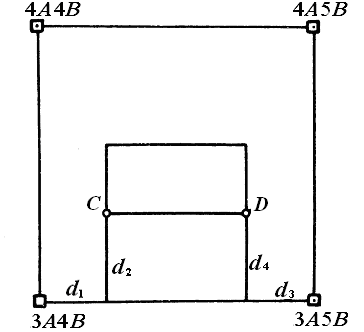Рис. 1.20. Вынос точек способом перпендикуляров При необходимости средняя квадратическая погрешность выноса на местность точки С может быть предвычислена по формул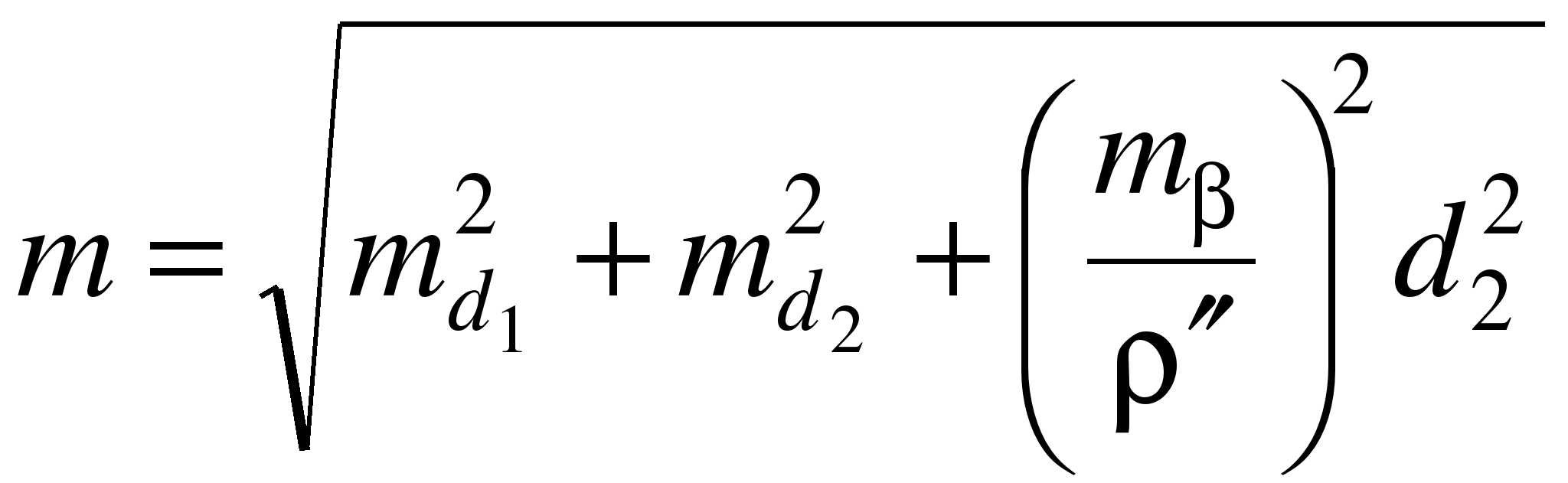е , (1.25) где и – средние квадратические погрешности отложения расстояний и ; – средняя квадратическая погрешность построения прямого угла. 1.6.2. Способ прямой угловой засечки На пересеченной местности линейные измерения и построения мерными лентами и рулетками затруднены или даже невозможны. В этом случае точки проекта рекомендуется выносить способом прямой угловой засечки, требующей построения на местности только двух горизонтальных углов. Преимущества способа проявляются и в том случае, когда расстояния до пунктов разбивочной сети велики.

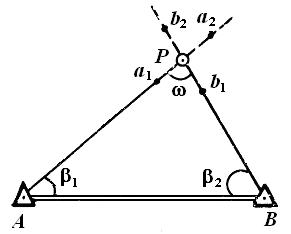
	Пример выноса точки Р в натуру способом прямой угловой засечки показан на рис. 1.21. От стороны разбивочной сети строительной площадки на пункте А откладывают угол и направление визирной оси фиксируют на местности точками и . На пункте В откладывают от этой же стороны угол и фиксируют направление точками и .
Рис. 1.21. Построение точки способом прямой угловой засечки

Между точками и , и натягивают проволоки и в точке их пересечения находят положение выносимой точки Р. Угол засечки должен быть от 30 до 150. Углы и вычисляют с использованием формул обратной геодезической задачи: (1.26) (1.27) ^