Запитання для самоперевірки:

7. Що називається вектором?

8. Який вектор називається нульовим?

9. Який вектор називається протилежним до даного?

10. Що називається сумою, різницею двох векторів?

11. Що називається добутком вектора на число?

12. Що називається скалярним добутком векторів?

13. Як знайти кут між двома векторами?

14. Які вектори називаються лінійно незалежними?

15. У якому випадку вектори утворююють базис?

Завдання для виконання:

Завдання 1. Знайти вектор , його довжину та кут між векторами і , якщо:

1. , ;

2. , ;

3. , ;

4. , ;

5. , ;

6. , ;

7. , ;

8. , ;

9. , ;

10. , .

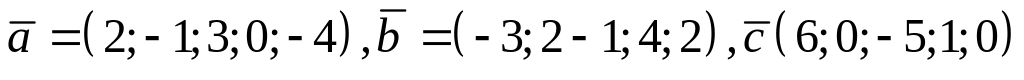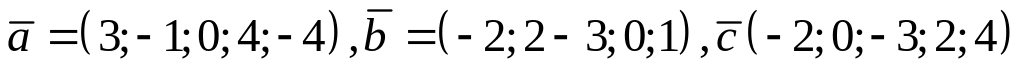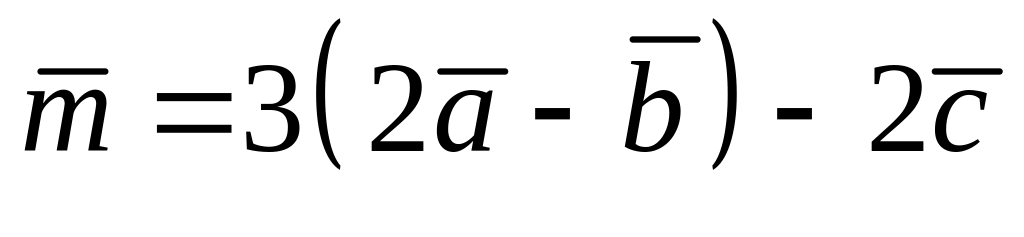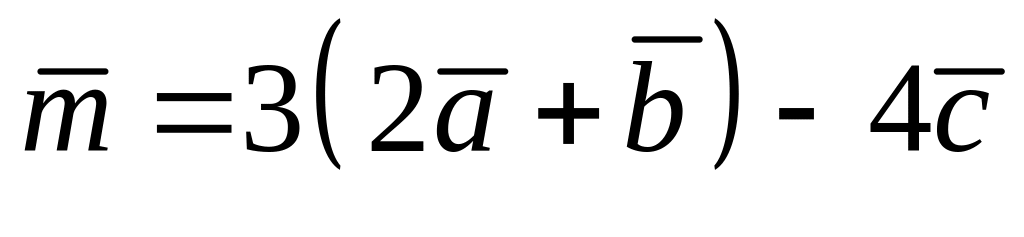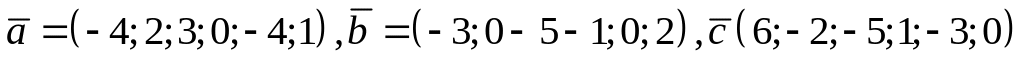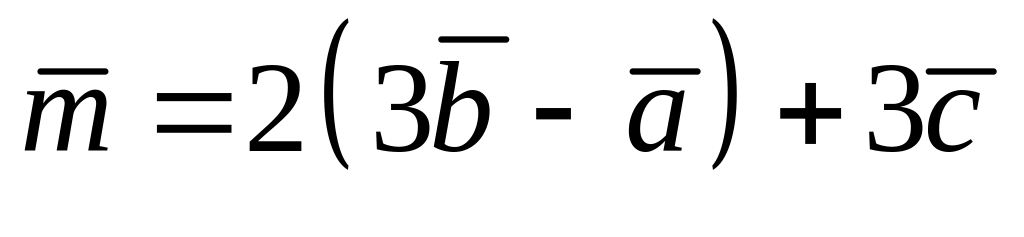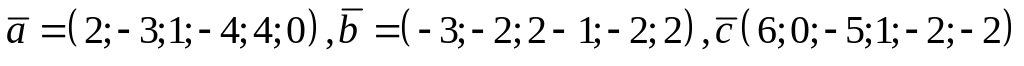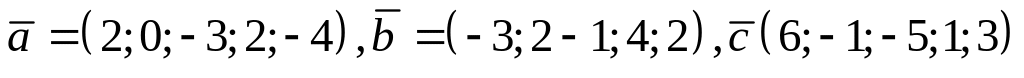Питання 2. Визначники і їх властивості.

Методичні рекомендації:

Визначником (детермінантом) 2-го порядку, записаним у вигляді виразу

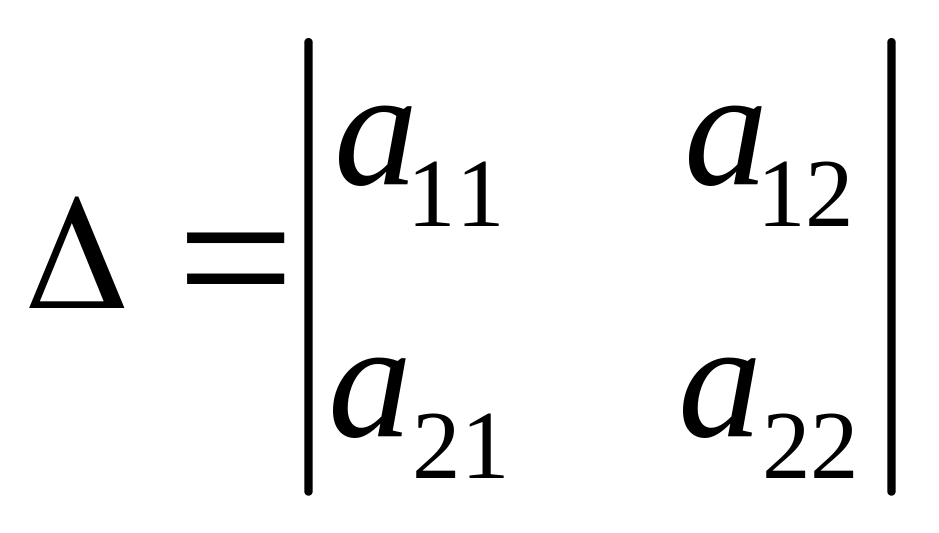
називається число .

Кожний елемент визначника можна записати у вигляді виразу ,

де і – номер рядка, j - номер стовпця.

Вираз:

– визначник третього порядку, причому

.

Способи обчислення визначників:

1. Обчислення визначників за правилом Саррюса (Сарруса, Саріуса):

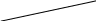
a ₁₁ a₁₂ a₁₃

a ₂₁ a₂₂ a

a₃₁ a₃₂ a₃₃

2. Правило дописування стовпців:

Для обчислення визначників вищого порядку використовують таке поняття як алгебраїчні доповнення.

Означенн: Мінором елемента визначника називатимемо новий визначник, який дістанемо з даного визначника викреслюванням рядка і стовпця, які містять даний елемент.

Мінор елемента –

Означення: Алгебраїчним доповненням елемента називається мінор цього елемента, який береться із знаком і позначається :

. Визначник п –го порядку має вигляд:

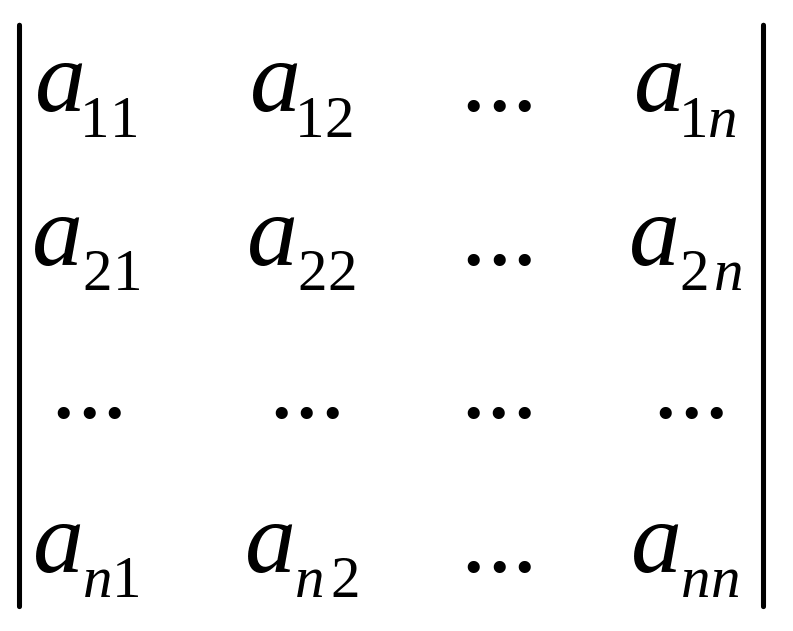
Теорема Лапласа: Визначник п – го порядку дорівнює сумі добутків елементів будь-якого рядка (або стовпця) на їхні відповідні алгебраїчні доповнення.

Властивості визначників.

1. Властивість рівноправності рядків і стовпців.

Визначник не змінюється, якщо в ньому рядки змінити на стовпці, а стовпці - на рядки.

2. Якщо у визначнику поміняти місцями два рядки (або стовпці), то визначник змінить знак на протилежний.

3. Визначник у якого елементи одного рядка (стовпця) відповідно рівні елементам другого рядка (стовпця), дорівнює нулю.

4. Якщо всі елементи рядка (стовпця) визначника мають спільний множник, то його можна винести за знак визначника.

5. Визначник, у якого елементи двох рядків (стовпців) є відповідно пропорційними, дорівнює нулю.

6. Якщо у визначнику всі елементи якого-небудь рядка (стовпця) є сумою двох доданків, то визначник дорівнює сумі двох визначників в одному з яких суми замінено їхніми першими доданками, а в другому - другими.

1. Якщо до елементів якого-небудь рядка (стовпця) відповідно додати елементи другого рядка (стовпця), помножені на одне й те саме число, то визначник не зміниться.

2. Визначник у якого всі елементи, розміщенні вище (або нижче) головної діагоналі є нулі, дорівнює добуток елементів головної діагоналі

Спосіб обчислення визначників порядку п≥3:

• розклад за елементами рядка або стовпця, причому вибираємо рядок або стовпець де є нулі;

• зводимо визначник до трикутної форми.

Приклад 1.

Обчислити визначник:

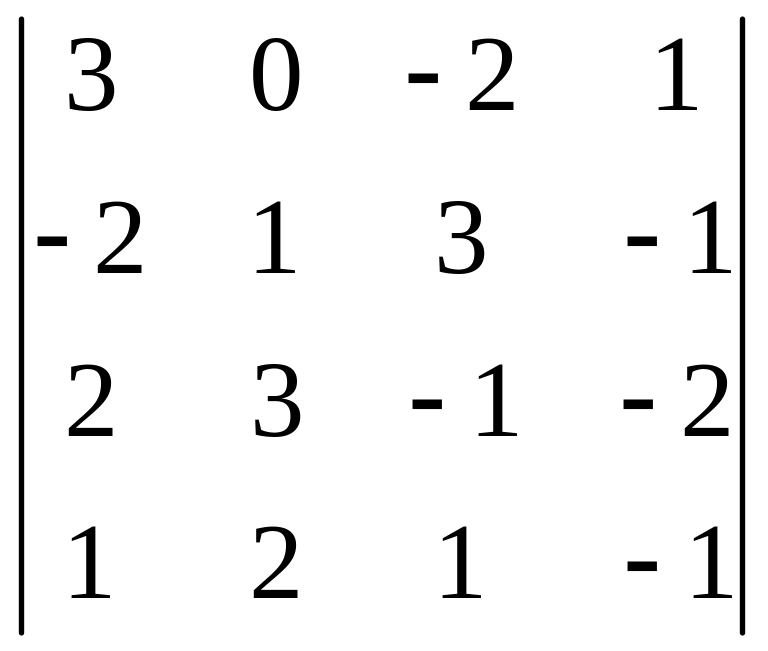
Розв’язання:

1 – ий спосіб:

2 – ий спосіб: