
- •Розділ 1
- •Самостійна робота №1
- •Методичні рекомендації:
- •Запитання для самоперевірки:
- •Завдання для виконання:
- •Методичні рекомендації:
- •Запитання для самоперевірки:
- •Завдання для виконання:
- •Література:
- •Розділ 2
- •Самостійна робота № 2
- •Методичні вказівки:
- •Запитання для самоперевірки:
- •Завдання для виконання:
- •Методичні вказівки:
- •Запитання для самоперевірки:
- •Завдання для виконання:
- •Література:
- •Розділ 3 самостійна робота № 3
- •Методичні вказівки:
- •Запитання для самоперевірки:
- •Завдання для виконання:
- •Методичні рекомендації:
- •Запитання для самоперевірки:
- •Завдання для виконання:
- •Методичні рекомендації:
- •Запитання для самоперевірки:
- •Завдання для виконання:
- •Методичні рекомендації:
- •Запитання для самоперевірки:
- •Завдання для виконання:
- •Література:
- •Запитання для самоперевірки:
- •Завдання для виконання:
- •Методичні рекомендації:
- •Запитання для самоперевірки:
- •Завдання для виконання:
- •Запитання для самоперевірки:
- •Завдання для виконання:
- •Література:
- •Розділ 5 Тема: Диференціальне та інтегральне числення самостійна робота № 5
- •Методичні рекомендації:
- •Запитання для самоперевірки:
- •Завдання для виконання:
- •Методичні рекомендації:
- •Запитання для самоперевірки:
- •Завдання для виконання
- •Методичні рекомендації:
- •Запитання для самоперевірки:
- •Завдання для виконання:
- •Питання 4. Диференціальні рівняння Методичні рекомендації:
- •Запитання для самоперевірки:
- •Завдання для виконання:
- •Література
- •Розділ 6 Тема: Елементи теорії ймовірностей та математичної статистики самостійна робота № 6
- •Методичні рекомендації:
- •Запитання для самоперевірки:
- •Завдання для виконання:
- •Питання 2. Залежні та незалежні випадкові події. Теореми множення ймовірностей. Методичні рекомендації:
- •Запитання для самоперевірки:
- •Завдання для виконання:
- •Питання 3. Дискретні випадкові величини, поняття про закон розподілу дискретної випадкової величини. Числові характеристики випадкових величин. Методичні рекомендації:
- •Запитання для самоперевірки:
- •Завдання для виконання:
- •Питання 4. Елементи математичної статистики Методичні рекомендації:
- •Запитання для самоперевірки:
- •Завдання для виконання:
- •Література:
Запитання для самоперевірки:
Що називається допустимим розв’язком ЗЛП?
Що таке базисний розв’язок ЗЛП?
Сформулюйте алгоритм розв’язування ЗЛП симплекс-методом.
Який стовпець береться за ключовий?
Як вибираємо ключовий рядок?
Як перевірити оптимальність розв’язку?
Завдання для виконання:
Завдання
2.
Знайти максимум лінійної форми, якщо
змінні
![]() задовольняють
наступні умови:
задовольняють
наступні умови:
1.
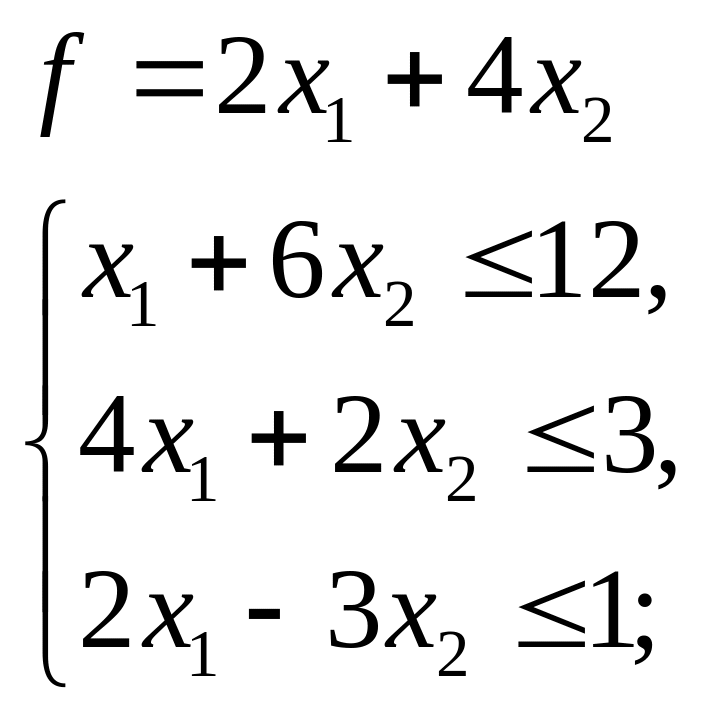 2.
2.

3.
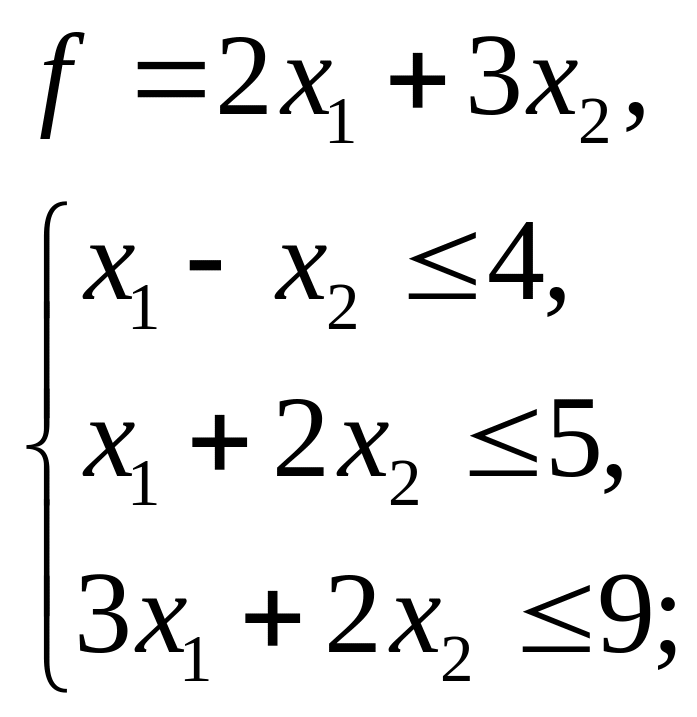 4.
4.

5.
 6.
6.

7.
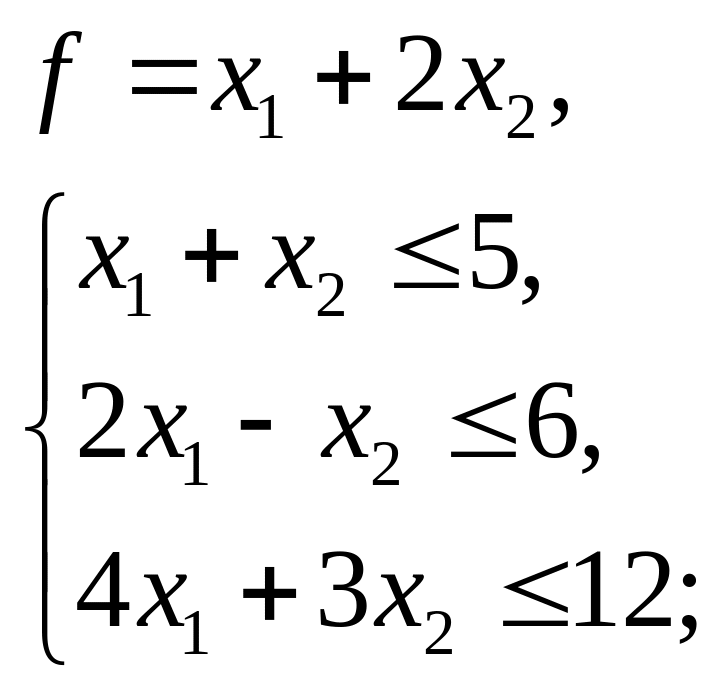 8.
8.
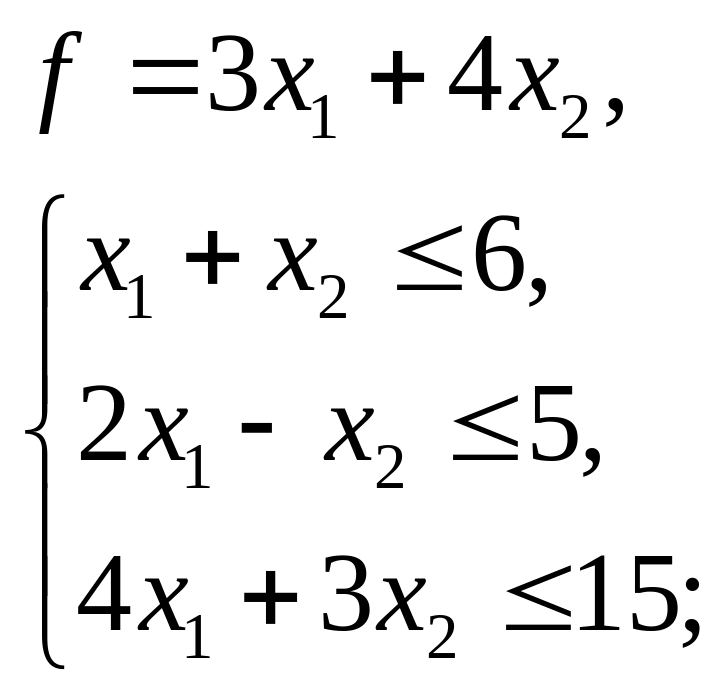
9.
 10.
10.
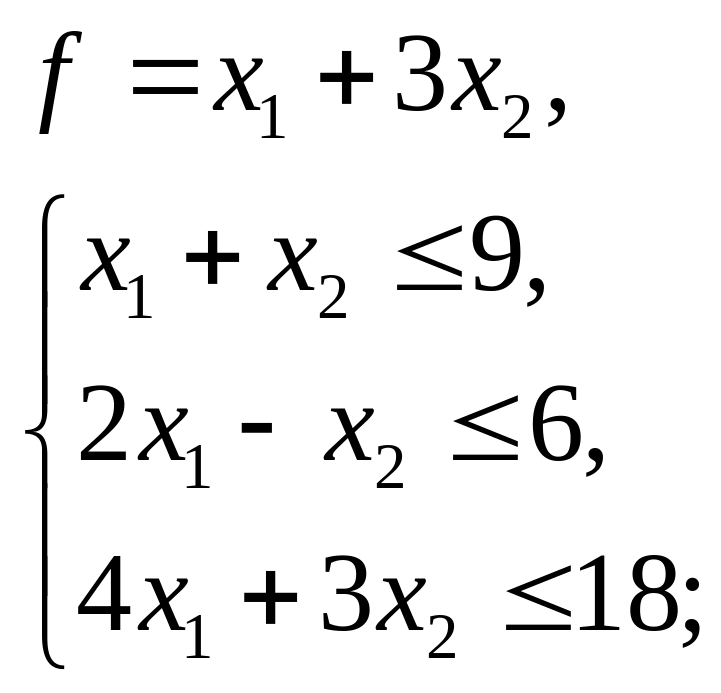
Питання 3. Транспортна задача.
Серед задач лінійного програмування особливе місце займає транспортна задача. Це обумовлено, по-перше, практичним значенням транспортної задачі, по-друге, транспортна задача має такі специфічні особливості, які дозволяють суттєво спростити загальні методи розв’язування. Формулюється транспортна задача так:
Є m
постачальників
![]() однорідної продукції. Максимальні
об’єми поставок продукції задані і
рівні
однорідної продукції. Максимальні
об’єми поставок продукції задані і
рівні
![]() .
Ця продукція використовується n
споживачами
.
Ця продукція використовується n
споживачами
![]() .
Об’єми споживання задані і рівні
.
Об’єми споживання задані і рівні
![]() .
Вартість перевезення одиниці продукції
від і-го
постачальника до j-го
споживача
відома для
.
Вартість перевезення одиниці продукції
від і-го
постачальника до j-го
споживача
відома для
![]() і дорівнює
.
Ставиться задача – встановити такі
об’єми перевезень
і дорівнює
.
Ставиться задача – встановити такі
об’єми перевезень
![]() від кожного постачальника
від кожного постачальника
![]() до кожного споживача
до кожного споживача
![]() ,
щоб сумарні затрати на перевезення
були мінімальними і потреби всіх
споживачів були задоволені (якщо це
можливо). Математична модель задачі
має вигляд:
,
щоб сумарні затрати на перевезення
були мінімальними і потреби всіх
споживачів були задоволені (якщо це
можливо). Математична модель задачі
має вигляд:

Якщо
виконується умова
![]() ,
то транспортна задача називається
задачею з правильним балансом або
закритою. В іншому випадку задача
називається задачею з неправильним
балансом або відкритою. Якщо потреби
споживачів перевищують можливості
постачальників, то вводиться m+1
пункт відправлення (постачання) з
можливістю
,
то транспортна задача називається
задачею з правильним балансом або
закритою. В іншому випадку задача
називається задачею з неправильним
балансом або відкритою. Якщо потреби
споживачів перевищують можливості
постачальників, то вводиться m+1
пункт відправлення (постачання) з
можливістю
![]() ,
якщо ж можливості постачальників більші
за потреби споживачів, то вводиться
,
якщо ж можливості постачальників більші
за потреби споживачів, то вводиться
![]() пункт споживання з потребою
пункт споживання з потребою
![]() .
.
При
розв’язанні транспортної задачі
базисні розв’язки (вершини многокутника)
грають особливу роль. Не вироджений
базисний розв’язок транспортної задачі
містить рівно
![]() ненульових перевезень
.
В іншому випадку базисний розв’язок
містить менше ніж
перевезень. Дані транспортної задачі
і обчислення заносяться в транспортну
таблицю. Від звичайної симплекс-таблиці
вона відрізняється тим, що в ній заповнені
тільки ті клітинки, де перевезення
ненульові. Вихідна транспортна таблиця
має вигляд:
ненульових перевезень
.
В іншому випадку базисний розв’язок
містить менше ніж
перевезень. Дані транспортної задачі
і обчислення заносяться в транспортну
таблицю. Від звичайної симплекс-таблиці
вона відрізняється тим, що в ній заповнені
тільки ті клітинки, де перевезення
ненульові. Вихідна транспортна таблиця
має вигляд:
|
Q1 |
Q2 |
... |
Qn |
аі |
Р1 |
|
|
|
|
|
Р2 |
|
|
|
|
|
... |
|
|
|
|
|
Pm |
|
|
|
|
|
bj |
|
|
|
|
|
Метод розв’язування транспортної задачі
Метод північно-західного кута (діагональний).
Даний
метод полягає в тому, що транспортну
таблицю заповнюють ненульовими
перевезеннями, починаючи з верхньої
лівої (північно-західної) клітинки. При
цьому розподіляють продукцію першого
постачальника, максимально задовольняючи
першого споживача, потім другого і т.д.
до повного розподілу продукції першого
постачальника. Потім розподіляють
продукцію другого постачальника,
причому якщо в деякому пункті
потреби не були задоволені, то поставки
будуть здійснюватись і від другого
постачальника. І так далі. Сума перевезень
в і-му
рядку рівна
![]() ,
в
,
в
![]() -
стовпці –
-
стовпці –
![]() .
Одержаний, таким чином, план перевезень
буде допустимим (опорним) розв’язком
транспортної задачі.
.
Одержаний, таким чином, план перевезень
буде допустимим (опорним) розв’язком
транспортної задачі.
Метод мінімального елемента (мінімальних тарифів).
Ідея
методу полягає в тому, щоб максимально
загрузити перевезеннями комунікації
з мінімальними транспортними витратами.
Тут таблицю будемо заповнювати, починаючи
з “дешевих” кліток. Метод реалізується
наступним чином: на першому кроці
визначаємо мінімальний елемент матриці
С.
Нехай це буде
![]() .
Покладаємо
.
Покладаємо
![]() .
Можливі два випадки:
.
Можливі два випадки:
1)
![]() (можливості
постачальника менші потреб споживача).
Тоді нулями заповнюється
(можливості
постачальника менші потреб споживача).
Тоді нулями заповнюється
![]() -
рядок, крім елемента
-
рядок, крім елемента
![]() .
Далі в обчисленнях
.
Далі в обчисленнях
![]() не
використовується.
не
використовується.
2)
![]() (можливості
постачальника більші потреб споживача).
Тоді нулями заповнюється
- стовпець, крім елемента
.
Далі не використовується споживач
(можливості
постачальника більші потреб споживача).
Тоді нулями заповнюється
- стовпець, крім елемента
.
Далі не використовується споживач
![]() .
.
На
другому кроці з матриці С
викреслюється відповідний рядок чи
стовпець. Одержуємо матрицю
![]() .
Вважаємо, що
.
Вважаємо, що
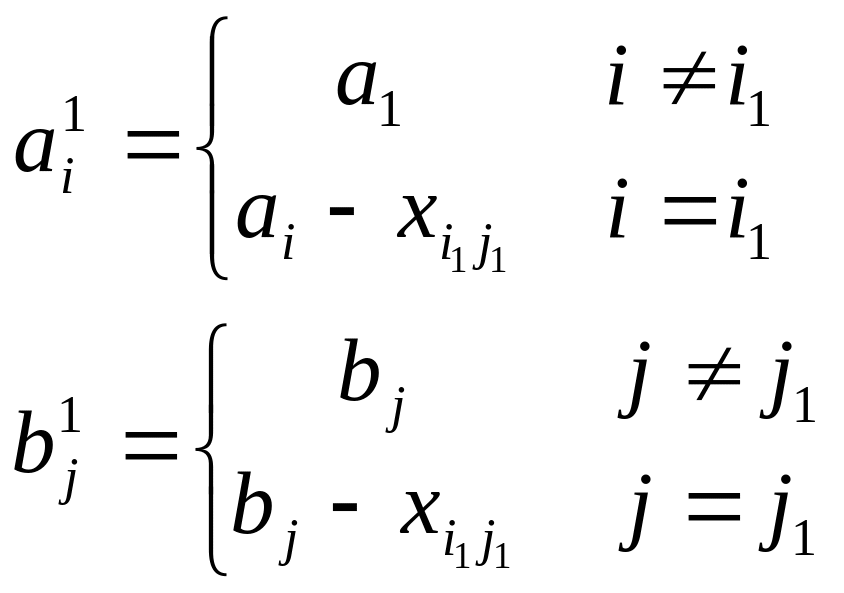
Другий крок – це виконання описаних операцій з матрицею . Продовжуємо до повного заповнення транспортної таблиці або викреслювання рядків чи стовпців матриці С.
Метод квадратів.
Щоб пояснити в чому полягає метод квадратів, введемо в розгляд поняття квадрата транспортної таблиці. Чотири клітинки, що розміщені в кутах виділеного прямокутника матриці перевезення, в яких хоча б на одній діагоналі розміщені базисні клітинки, будемо називати квадратом. Квадрат будемо називати неправильним, якщо сума вартостей базисних клітинок діагоналі білтша суми двох інших вартостей, і правильним, якщо сума менша. В іншому випадку квадрат називається нейтральним. Метод квадратів базується на такій необхідній умові оптимальності опрного плану.
Теорема: В оптимальній матриці перевезень не існує неправильних квадратів, тобто сума вартостей всіх базисних клітинок повинна бути меншою суми двох інших вартостей.
Отже, всі неправильні квадрати слід замінити правильними. Перетворення здійснюється у такий спосіб: за базисною діагоналлю знаходимо найменше базисне значення. Від базисних значень базисної діагоналлі, а до значень іншої діагоналлі додаємо це число. Відмітимо, що будь-яка заміна неправильного квадрата правильним зменшує загальну вартість перевезень.
Зауваження: Якщо виявиться, що в таблиці не один, а декілька неправильних квадратів, то необхідно послідовно замінити неправильні квадрати на правильні. Якщо в матриці перевезень немає неправильних квадратів, то знайдений розв’язок необхідно перевірити за критерієм оптимальності на оптимальність, оскільки відсутність неправильних квадратів ще не гарантує оптимальності розв’язку. Якщо всі неправильні квадрати виписати важко, то слід брати до уваги ті клітинки, в яких порушується умова оптимальності.
Метод потенціалів.
Нехай
![]() - потенціали пунктів
- потенціали пунктів
![]()
![]() .
Назвемо величину
.
Назвемо величину
![]() відносною оцінкою змінної
.
відносною оцінкою змінної
.
Теорема: Для того, щоб опорний план був оптимальним, необхідно і достатньо, щоб виконувались умови:
![]() – для
базисних клітинок;
– для
базисних клітинок;
![]() – для
вільних клітинок.
– для
вільних клітинок.
Тоді
базисний розв’язок
![]() оптимальний тоді і тільки тоді, коли
існують потенціали
такі, що відносні оцінки
оптимальний тоді і тільки тоді, коли
існують потенціали
такі, що відносні оцінки
![]() для базисних (зайнятих) кліток транспортної
таблиці і
для базисних (зайнятих) кліток транспортної
таблиці і
![]() для не базисних (вільних) кліток. Суть
методу потенціалів полягає в наступному:
для не базисних (вільних) кліток. Суть
методу потенціалів полягає в наступному:
В якості першого наближення до оптимального розв’язку береться довільний початковий базисний розв’язок (побудований будь-яким методом).
Визначаються потенціали так, щоб в кожній базисній клітці виконувалась умова або
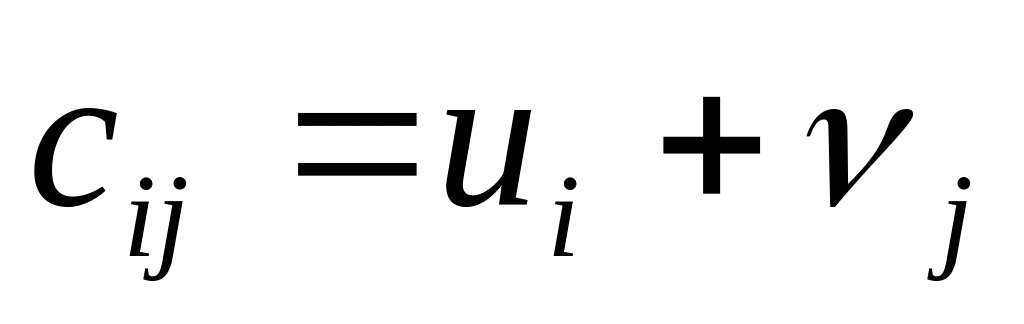 .
Відмітимо, що така система містить
рівняння (по кількості базисних кліток)
і
.
Відмітимо, що така система містить
рівняння (по кількості базисних кліток)
і
 невідомих. Тому одну із змінних задають
довільно (наприклад
невідомих. Тому одну із змінних задають
довільно (наприклад
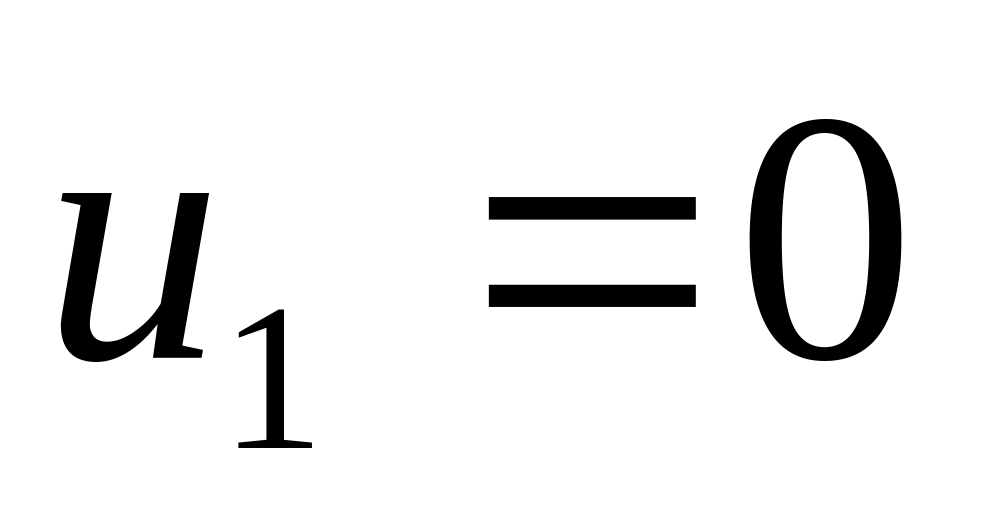 ),
інші знаходять з вказаної системи.
),
інші знаходять з вказаної системи.Обчислюються відносні оцінки
 для не базисних (вільних кліток). Якщо
хоча б для однієї з цих кліток
для не базисних (вільних кліток). Якщо
хоча б для однієї з цих кліток
 ,
то досліджуваний базисний розв’язок
можна покращити, вводячи в число
базисних одну із вказаних кліток
(зазвичай ту, для якої відносна оцінка
мінімальна). Нехай це
,
то досліджуваний базисний розв’язок
можна покращити, вводячи в число
базисних одну із вказаних кліток
(зазвичай ту, для якої відносна оцінка
мінімальна). Нехай це
 .
Розглянемо питання про те, яка із
базисних кліток виводиться із числа
базису. Із кліток транспортної таблиці
створюємо цикл (замкнутий ланцюжок)
так, щоб він містив не базисну клітку,
а інші клітки були базисними. Циклом
в матриці перевезень будемо називати
замкнену ламану лінію, вершини якої
розміщені в клітинках матриці перевезень
і з кожної вершини виходять два відрізки:
один по рядку, другий по стовпцю. Можливі
цикли зображені на малюнку:
.
Розглянемо питання про те, яка із
базисних кліток виводиться із числа
базису. Із кліток транспортної таблиці
створюємо цикл (замкнутий ланцюжок)
так, щоб він містив не базисну клітку,
а інші клітки були базисними. Циклом
в матриці перевезень будемо називати
замкнену ламану лінію, вершини якої
розміщені в клітинках матриці перевезень
і з кожної вершини виходять два відрізки:
один по рядку, другий по стовпцю. Можливі
цикли зображені на малюнку:

Перпендикулярні
ламані циклу можуть перетинатись, а
точки перетину не будуть вершинами
циклу. Вершини одного і того самого
відрізку циклу будемо називати сусідніми.
Помітимо клітки циклу наступним чином:
небазисну знаком “+”, інші знаком “+”
чи “-”, але так, щоб сусідні по рядку
чи по стовпцю клітинки мали різні знаки.
Збільшуємо тепер об’єм перевезень, що
знаходяться в клітинках з знаком “+”
на величину
![]() ,
а об’єм перевезень, що стоять в клітинках
з знаком “-” зменшимо на ту ж величину.
Очевидно, що в якості
слід вибрати мінімум серед від’ємних
кліток, тоді в результаті такого
перерозподілу вантажу одна із базисних
кліток стане вільною, а клітка
увійде в базис. Слід зауважити, що для
кожної вільної клітинки існує лише
один цикл перерахунку. Значення базисних
клітинок, які не бралт участі в перерахунку
не змінюється.
,
а об’єм перевезень, що стоять в клітинках
з знаком “-” зменшимо на ту ж величину.
Очевидно, що в якості
слід вибрати мінімум серед від’ємних
кліток, тоді в результаті такого
перерозподілу вантажу одна із базисних
кліток стане вільною, а клітка
увійде в базис. Слід зауважити, що для
кожної вільної клітинки існує лише
один цикл перерахунку. Значення базисних
клітинок, які не бралт участі в перерахунку
не змінюється.
4) За допомогою описаної процедури перерозподілу вантажів по циклу, одержимо новий базисний розв’язок, який треба перевірити на оптимальність. Процес повторюється і т.д. аж поки для певного базисного розв’язку не буде виконаний критерій оптимальності.
В невиродженому випадку метод потенціалів приводить до оптимального розв’язку за скінченну кількість кроків. У виродженому випадку, якщо зайнятих клітинок менше ніж , можливе зациклювання, для попередження якого необхідні додаткові міри.
