
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФИЛИАЛ ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ
«МЭИ»» в г. Смоленске
Кафедра вычислительной техники
Расчетное задание
по курсу «Теория передачи информации»
тема: «Построение кодирующих и декодирующих устройств»
Группа: АС-10
Студент: Крылов О. А.
Преподаватель: Пучков Ю. И.
Вариант: 1А
Смоленск, 2013
Содержание
Введение 3
Задание на расчет 4
Описание алгоритмов кодирования и декодирования 5
Решение поставленной задачи 6
Вычисление энтропии и избыточности сообщений 7
Пример декодирования унарного кода 8
Заключение 10
Список использованной литературы 11
Приложение 12
Введение
Когда мы передаем сообщение от источника к приемнику, при передаче данных может произойти ошибка (помехи, неисправность оборудования и пр.). Чтобы обнаружить и исправить ошибку, применяют помехоустойчивое кодирование, т.е. кодируют сообщение таким образом, чтобы принимающая сторона знала, произошла ошибка или нет, и при могла исправить ошибки в случае их возникновения.
По сути, кодирование — это добавление к исходной информации дополнительной, проверочной, информации. Для кодирования на передающей стороне используются кодер, а на принимающей стороне — используют декодер для получения исходного сообщения.
Проверка четности – очень простой метод для обнаружения ошибок в передаваемом пакете данных. С помощью данного кода мы не можем восстановить данные, но можем обнаружить только лишь одиночную ошибку.
Избыточность кода — это количество проверочной информации в сообщении, Рассчитываемое по формуле:
, (1)
где r – количество избыточных данных, n – длина исходной комбинации, k – длина кодовой комбинации
Энтропией системы называется сумма произведений вероятностей различных состояний системы на логарифмы этих вероятностей, взятая с обратным знаком:
![]() ,
(2)
,
(2)
Для представления каждого символа алфавита в бинарном виде будем использовать американский стандартный код для обмена информацией (ASCII). Таблица символов ASCII приведена в приложении.
Для расчета приведенных формул использован математический пакет MATCHAD.
Задание на расчет
Закодировать, используя код с проверкой на четность, следующую фразу русского языка: «Теория передачи дискретных сообщений.»;
Приняв частость повторения в предложенной фразе букв за их вероятности, вычислить энтропию сообщения;
Определить избыточность передаваемой информации;
Составить и описать алгоритмы кодирования и декодирования для предложенного кода;
Привести закодированный вариант первой половины предложенной фразы и ее декодирование.
Описание алгоритмов кодирования и декодирования
Алгоритм кодирования кодом с проверкой на четность
В каждом пакете данных есть один бит четности, или, так называемый, паритетный бит. Этот бит устанавливается во время записи (или отправки) данных, и затем рассчитывается и сравнивается во время чтения (получения) данных. Он равен сумме по модулю 2 всех бит данных в пакете. То есть число единиц в пакете всегда будет четно. Изменение этого бита (например с 0 на 1) сообщает о возникшей ошибке.
На
рис. 1 показана структурная схемы кодера
для данного кода.
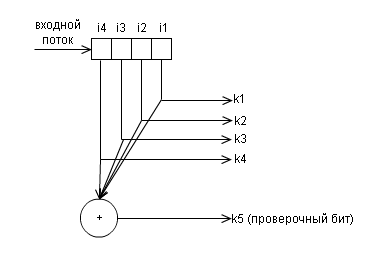
Рисунок 1 – структурная схема кодера
Алгоритм декодирования унарного кода
Декодирование будет осуществляться следующим образом: в декодируемой последовательности вычисляется новый бит паритета и сравнивается с принятым. Если бит изменился, то сообщение передано с ошибкой. Иначе отбрасываем последний бит и по таблице символов находим соответствующий данному коду символ.
На рис. 2 показана структурная схема декодера для данного кода.
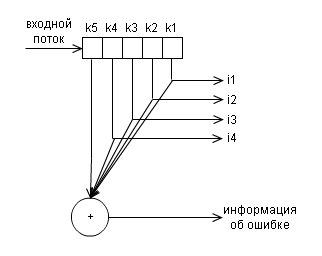
Рисунок 2 – структурная схема декодера
