1.5 Статистична обробка даних

Розрахуємо коефіцієнти дисперсії, кореляції та коваріації.

Визначимо коефіцієнти дисперсії значень часу та функції, за такими формулами:

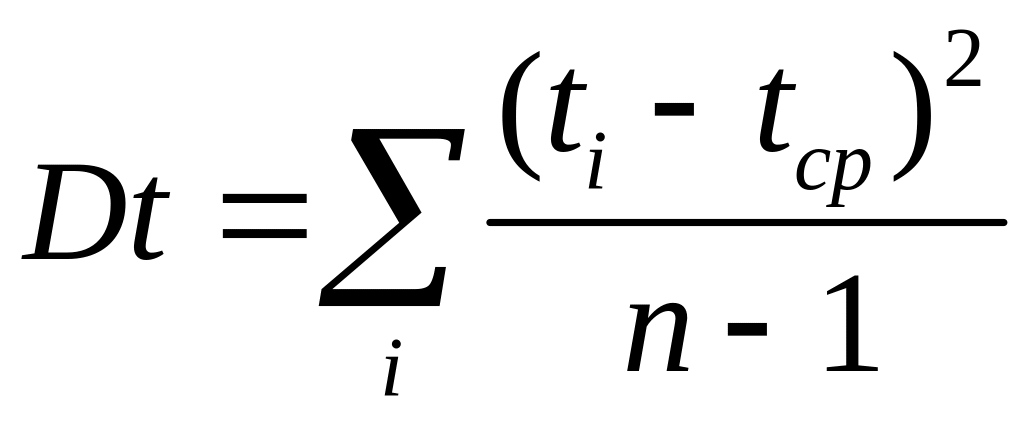
Коефіцієнт коваріації за такою формулою:

Коефіцієнт кореляції за такою формулою:

Використовуючи математичний пакет Matlab, виконаємо розрахунок і нижче наведено лістинг програмного модуля:

clear;

load data.mat;

n=121;

i=1:n;

tser=sum(n1t)/n;

fser=sum(n1ut)/n;

cov=sum((n1t-tser).*(n1ut-fser))/(n-1)

Dt=sum((n1t-tser).^2)/(n-1);

Du=sum((n1ut-fser).^2)/(n-1)

r=cov/sqrt(Dt*Du)

Після виконаного розрахунку отримаємо:

cov = 0.4674;

Dt = 1.7822e+003;

Du = 0.4754;

r = 0.0161.

1.6 Знаходження періодограми сигналів

Періодограма сигналу – це оцінка спектральної щільності потужності (СЩП) сигналу по певній кількості відліків реалізації випадкового процесу, заснована на обчисленні квадрата модуля перетворення Фур'є послідовності даних з використанням статистичного усереднення:

де X_T (iω) – перетворення Фур'є функції x(t) на кінцевому часовому інтервалі, T_r –інтервал фінітності, E – оператор статистичного усереднення (математичне очікування).

Слід зауважити, що дане співвідношення виконується тільки при нескінченному числі використовуваних відрахунків, тому при будь-якому кінцевому N періодограмна оцінка спектральної щільності потужності виявляється зміщеною – виходить, що всередині суми співвідношення кореляційна функція сигналу множиться на трикутну вагову функцію.

Для побудови періодограми сигналу розрахуємо середній спектр потужності , що розраховується за такими залежностями:

де n – загальна кількість точок.

Використовуючи математичний пакет Matlab, виконаємо розрахунок і побудуємо періодограму.

Нижче наведено лістинг програмного модуля:

clear;

load data.mat;

n=121;

for k=1:n

w(k,1)=(2*pi*(k))/n;

U(k,1)=(1/sqrt(n))*sum(n1ut.*exp(-j*w(k).*n1t));

end

Ui=imag(U);

Ur=real(U);

subplot(1,2,1);

plot(w,Ui);

title('а)');

xlabel('Нормована частота (Гц)');

ylabel('Спектр щільності (Дб/Гц)');

grid on

subplot(1,2,2);

plot(w,Ur);

title('б)');

xlabel('Нoрмована частота (Гц)');

ylabel('Спектр щільності (Дб/Гц)');

grid on

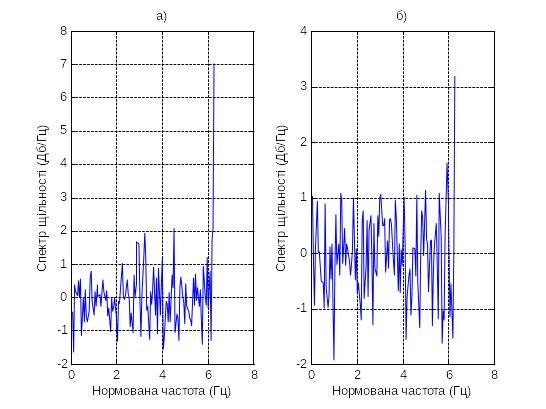
Рис. 1.4 - Періодограма вхідного сигналу U(t), де а) – уявна частина,

б) – дійсна частина

1.7 Вибір оптимальної моделі

Оптимальна модель вибирається згідно критерію, що відповідає похибці побудови моделі до вихідної характеристики в співвідношенні до кількості аналізованих даних:

Використовуючи математичний пакет Matlab, виконаємо розрахунок і запишемо результати до таблиці 5.2.

Нижче наведено лістинг програмного модуля:

SPol_Ut=sqrt((sum(n1ut-rot90(f)).^2)/(n-2))

SCheb_Ut=sqrt((sum(n1ut-Cheb').^2)/(n-2))

SFur_Ut=sqrt((sum(n1ut-FS).^2)/(n-2))

Оптимальні значення моделей

Таблиця 1.2

Вид функції	Поліном	Поліном Чебишева	Функція Фур’є
Значення критерію	0.1115	1.6237	0.0027

Як видно з таблиці 2.2, значення критерію мінімальне у тому випадку, коли апроксимуючою функцією виступає перетворення Фур’є, отже модель побудована даним чином буде оптимальною.