Лекция №11 определение периода приработки и технического ресурса

Обработка статистических данных эксплуатации об отказах и неисправностях показывает, что для многих систем интенсивность отказов λ(t) как функция времени имеет характер, показанный на рис. 7.5. Первый период соответствует отрезку (0, t₁) и характеризуется уменьшением λ(t). Второй период— отрезок (t₁, t₂) характеризуется практическим постоянством λ(t). Третий период — (t₂ , ∞) — характеризуется возрастанием λ(t).

λ

0 t₁ t₂ t

рис. 7.5 Изменение интенсивности отказов в зависимости от срока эксплуатации

При таком характере изменения λ(t) одним из основных вопросов является выбор такого момента t_нач начала эксплуатации, при котором объект обладал бы максимально возможным уровнем надежности. Промежуток времени (0, t_нач) называется периодом приработки объекта. Обозначим период приработки t_пр. Очевидно, величина t_пр соответствует такому моменту t, в который

(7.22)

Такой подход справедлив в случае, если время t_э эксплуатации объекта, в течение которого требуется обеспечить его безотказную работу, удовлетворяет условию:

τ_э≤(t₁, t₂) (7.23)

Если условие (7.23) не выполняется, то период приработки, определяемый по (7.22), нельзя считать оптимальным, так как его реализация может привести к необоснованному снижению надежности объекта при последующей эксплуатации.

Задача определения периода приработки в общем виде может быть сформулирована следующим образом.. Период приработки оптимален, если для поступившего в эксплуатацию объекта по окончании времени t_пр показатель надежности, определенный на интервале τ_э, установленного времени эксплуатации, имеет максимальное значение.

В качестве показателя надежности примем вероятность безотказной работы объекта в течение времени τ_э. Обозначим эту вероятность p(t_пр,t_пр + τ_э). Тогда

p(t_пр,t_пр + τ_э)=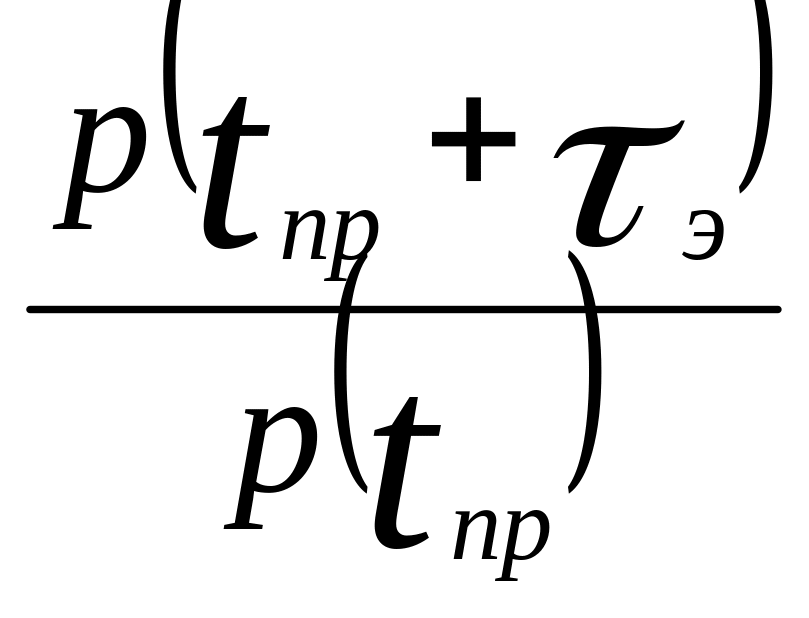 (7.24)

где p(t_пр + τ_э) – вероятность безотказной работы объекта в течение времени t_пр + τ_э;

p(t_пр) – вероятность безотказной работы объекта за время t_пр.

В общем случае

p(t_пр,t_пр + τ_э)=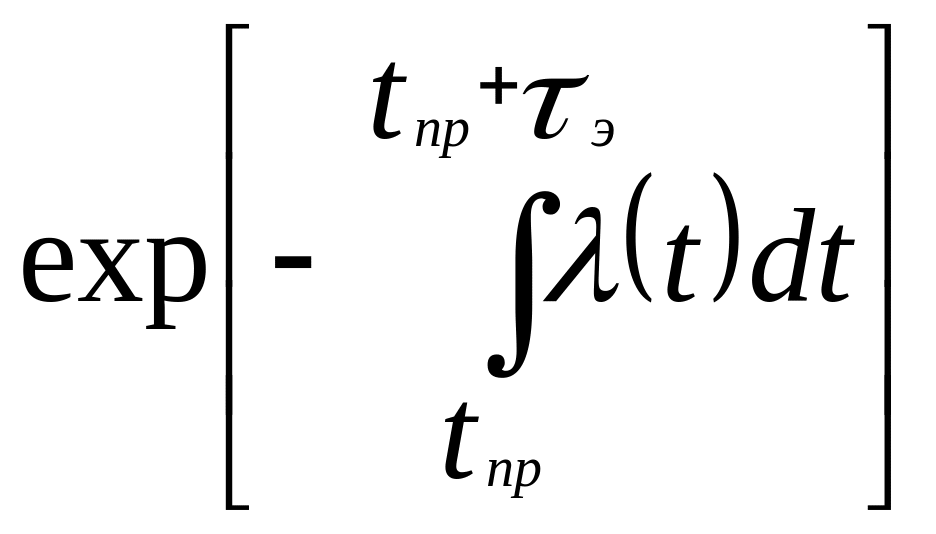 (7.25)

Период приработки, если интенсивность отказов λ(t) имеет зависимость, соответствующую рис. 7.5, будет иметь оптимум при условии

.

Решение этого уравнения соответствует условию:

λ(t_пр+τ_э)λ(t_пр)=0 (7.26)

Из (7.26) следует, что если проводить выбор приработки путем максимизации вероятности p(t_пр,t_пр + τ_э), то величина t_пр будет иметь оптимальное значение при условии равенства интенсивности отказов в начале и в конце эксплуатации.

Таким образом, если λ = const, выбор величины t не влияет на вероятность p(t_np,t_np + τ_э) и можно принять t_пр = 0. При монотонно возрастающем характере зависимости λ(t) необходимо назначить t_np = 0. Если же λ(t) — монотонно убывающая функция, необходимо выбрать наибольшее из возможных значений t_пр, обеспечивающих эксплуатацию объекта на протяжении времени τ_э. Так как эти случаи приводят к тривиальным решениям, рассмотрим случай, когда λ(t) - вогнутая функция (рис. 7.5, например).

Из сказанного раньше следует, что величина t зависит от длительности времени эксплуатации. Поэтому, если уравнение (7.26) дополнить некоторым условием, включающим переменную τ_э, то представляется возможным определить и время эксплуатации τ_э.

λ (t_пр+τ_э)λ(t_пр)=0

=р_треб (7.27)

При наличии аналитической зависимости λ(t) система уравнений (7.27) может быть решена аналитически, если же зависимость λ(t) представлена только графиком - решение можно получить графически.