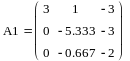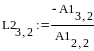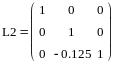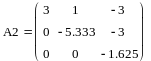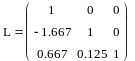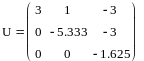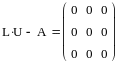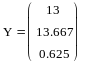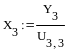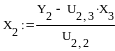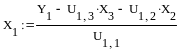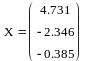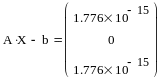- •Для решения системы линейных алгебраических уравнений Описание метода
- •Требования к отчету
- •Задания для самостоятельной работы:
- •Описание метода
- •Пример:
- •Требования к отчету
- •Задания для самостоятельной работы
- •Описание метода
- •Требования к отчету
- •Задания для самостоятельной работы
- •Библиографический список
- •Методы решения систем линейных алгебраических уравнений
- •153005, Г. Иваново, ул. Рабфаковская, 34.
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования
«Ивановский государственный энергетический
университет имени В.И. Ленина»
Пяртли А.С., Кузнецова Д.С.
Методы решения систем линейных
алгебраических уравнений
Методическое пособие к выполнению
лабораторных работ
Иваново 2013
УДК
П99
Пяртли А.С., Кузнецова Д.С. Методы решения систем линейных алгебраических уравнений: Метод. пособие/ ФГБОУВПО «Ивановский государственный энергетический университет имени В.И. Ленина». – Иваново, 2013. – 60 с.
Методическое пособие создано для студентов, обучающихся по направлению 010400 «Прикладная математика и информатика» изучающих дисциплину «Алгебра и аналитическая геометрия». Цель пособия – помощь студентам при подготовке к лабораторным работам по теме «Решение систем линейных уравнений» и при их выполнении. В пособии приведены также системы линейных уравнений, которые студенты должны решить на лабораторной работе. Достаточно подробно рассмотрена последовательность действий, выполняемых при решении систем уравнений тем или иным методом. Решение систем основано на разложении матрицы коэффициентов в произведение двух или трех сомножителей, а именно, LU-разложение, LUP-разложение, QR-разложение, разложение Холецкого. Пособие может быть также использовано при изучении численных методов студентами других специальностей.
Библиогр.: 8 назв.
Печатается по решению редакционно-издательского совета ФГБОУВПО «Ивановский государственный энергетический университет имени В.И.Ленина»
Научный редактор
В.Ю.Киселев
Рецензент
кафедра высшей математики ФГБОУВПО «Ивановский государственный энергетический университет имени В.И.Ленина»
© А.С. Пяртли, Д.С. Кузнецова, 2013
ОГЛАВЛЕНИЕ
1. LU-разложение матрицы и его использование 8
для решения системы линейных алгебраических уравнений 8
Описание метода 8
Лабораторная работа №1 11
Цель работы: 12
Постановка задачи 12
Ход лабораторной работы: 12
Пример 14
Требования к отчету 17
Задания для самостоятельной работы: 17
Описание метода 21
Лабораторная работа №2 25
Цель работы: 25
Постановка задачи 26
Ход лабораторной работы 26
Пример: 27
Требования к отчету 32
Задания для самостоятельной работы 33
3. QR-разложение матрицы и его использование для решения системы линейных алгебраических уравнений 36
Описание метода 36
Лабораторная работа №3 40
Цель работы: 40
Постановка задачи 40
Ход лабораторной работы 41
Пример 42
Требования к отчету 49
Задания для самостоятельной работы 49
4. Разложение Холецкого симметричной матрицы коэффициентов и его использование для решения системы линейных алгебраических уравнений 53
Описание метода 53
Лабораторная работа №4 55
Цель работы: 55
Постановка задачи 55
Ход лабораторной работы 56
Пример 56
Требования к отчету 58
Задания для самостоятельной работы 58
Введение
Проблема численного решения систем линейных алгебраических уравнений интересует математиков уже несколько столетий. Первые результаты появились в XVIII веке. В 1750 году Г. Крамер (1704 – 1752) опубликовал способ решения систем линейных алгебраических уравнений с ненулевым определителем основной матрицы, известный как правило Крамера. Гаусс в 1809 году опубликовал работу, посвященную движению небесных тел, в которой был изложен метод для решения линейных систем, известный как метод исключения.
В 40-х годах XX века с появлением компьютеров сильно возрос интерес к численным методам. Тогда же началось активное исследование существующих методов для их реализации на ЭВМ и предпринимались активные попытки увеличить их точность. Вплоть до 80-х годов решение вычислительных задач было ограничено ресурсами ЭВМ, поэтому особое значение придавалось экономичности алгоритмов. В настоящее время ограничения по оперативной памяти и быстродействию ЭВМ потеряли актуальность в связи с появлением относительно дешевых мини- и суперкомпьютеров, но только при небольшом числе переменных систему линейных уравнений можно решать любым способом. Если же число переменных большое, то при неудачном выборе метода решения линейной системы уравнений время, затраченное компьютером на вычисления, может быть слишком большим. Для решения системы из n уравнений с n неизвестными приходится выполнять порядка n3 операций. Кроме того, при большом числе операций могут сильно возрастать погрешности, связанные с округлениями в компьютере результата каждой операции.
Для решения системы n линейных уравнений с n неизвестными и невырожденной матрицей коэффициентов используется разложение матрицы коэффициентов в произведение более простых матриц. Пусть дана система линейных уравнений
![]() ,
(1)
,
(1)
где
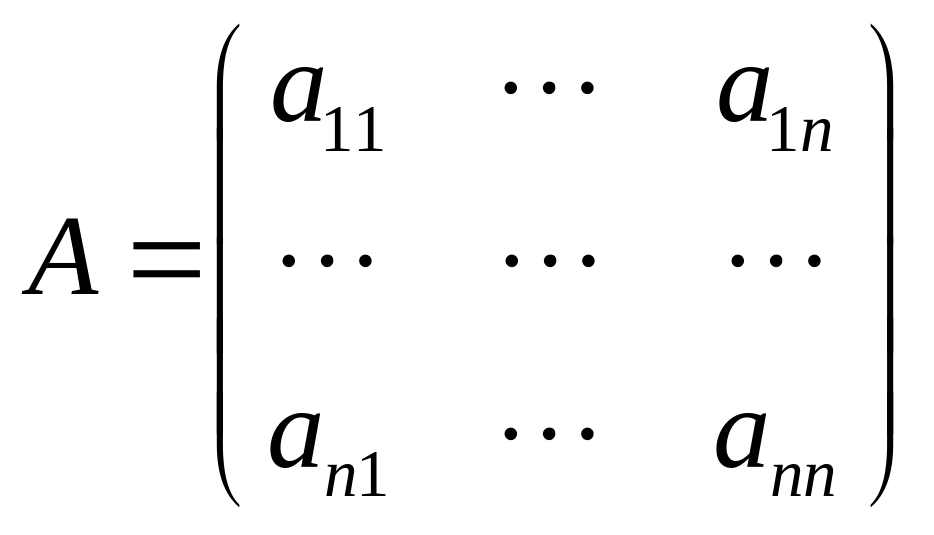 ,
,
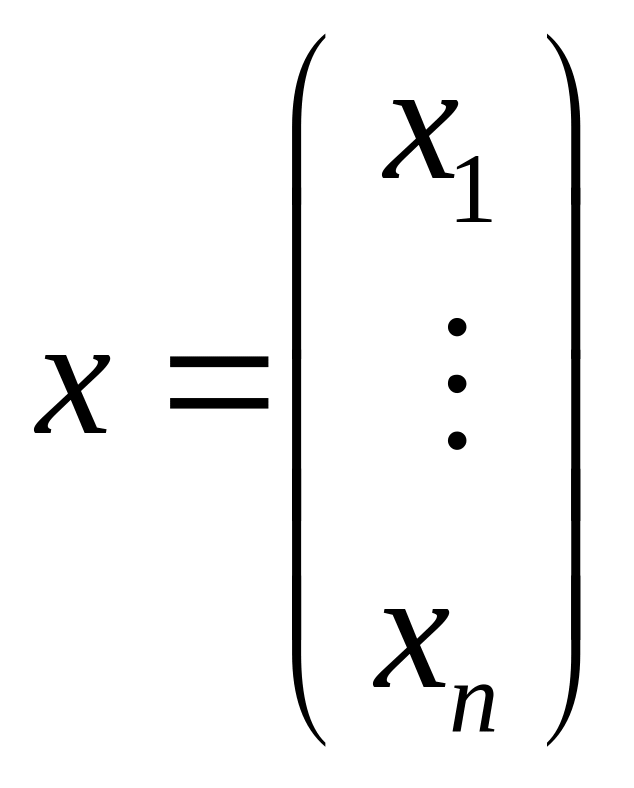 ,
,
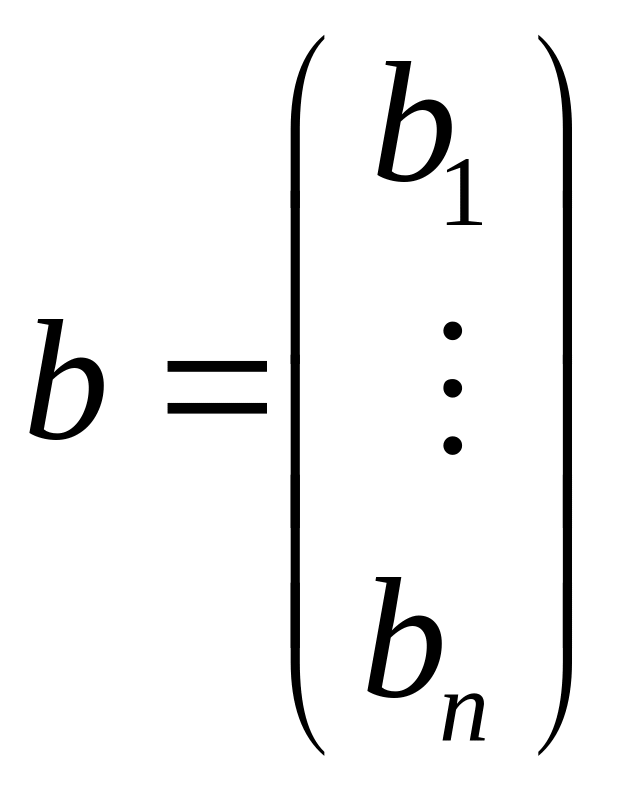 – соответственно матрица коэффициентов,
столбец неизвестных и столбец свободных
членов. Пусть матрица
– соответственно матрица коэффициентов,
столбец неизвестных и столбец свободных
членов. Пусть матрица
![]() невырожденная, т.е.
невырожденная, т.е.
![]() .
Пусть
.
Пусть
![]() ,
где
,
где
![]() и
и
![]() – квадратные матрицы порядка n,
такие, что системы
– квадратные матрицы порядка n,
такие, что системы
![]() ,
,
![]() легко решаются. Тогда система (1) принимает
вид
легко решаются. Тогда система (1) принимает
вид
![]() .
(2)
.
(2)
Обозначим
![]() .
Система (2) запишется в виде
.
Система (2) запишется в виде
![]() ,
и ее решение легко найти. Пусть ее решение
уже найдено. Тогда из системы
,
и ее решение легко найти. Пусть ее решение
уже найдено. Тогда из системы
![]() находим x.
Эта система тоже легко решается. Мы
рассмотрим только четыре способа
разложения матриц, разложения LU,
LUP,
QR
и Холецкого. Разложения LU
и QR
можно применять для любых систем,
разложение Холецкого применимо только
к системам с симметрической положительно
определенной матрицей коэффициентов.
Задумываться о выборе определенного
метода имеет смысл в том случае, если
необходимо найти решение системы
линейных уравнений с большим числом
неизвестных. Для систем с небольшим
числом неизвестных выбор метода не
играет существенной роли.
находим x.
Эта система тоже легко решается. Мы
рассмотрим только четыре способа
разложения матриц, разложения LU,
LUP,
QR
и Холецкого. Разложения LU
и QR
можно применять для любых систем,
разложение Холецкого применимо только
к системам с симметрической положительно
определенной матрицей коэффициентов.
Задумываться о выборе определенного
метода имеет смысл в том случае, если
необходимо найти решение системы
линейных уравнений с большим числом
неизвестных. Для систем с небольшим
числом неизвестных выбор метода не
играет существенной роли.
1. LU-разложение матрицы и его использование
Для решения системы линейных алгебраических уравнений Описание метода
Метод LU-разложения
является одной из разновидностей метода
Гаусса и заключается в представлении
матрицы коэффициентов
A
в виде
![]() ,
где L
– нижняя треугольная матрица с единицами
на диагонали, U
– верхняя треугольная матрица:
,
где L
– нижняя треугольная матрица с единицами
на диагонали, U
– верхняя треугольная матрица:
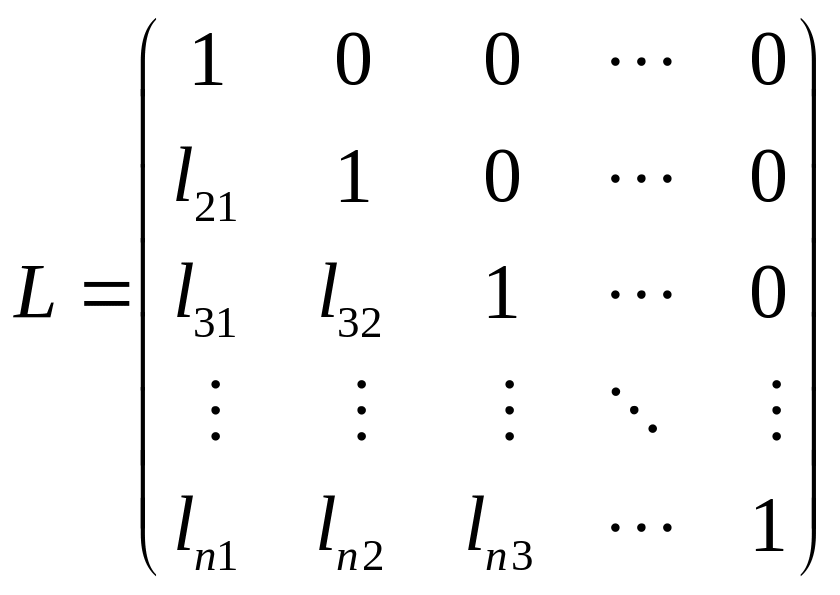 ,
,
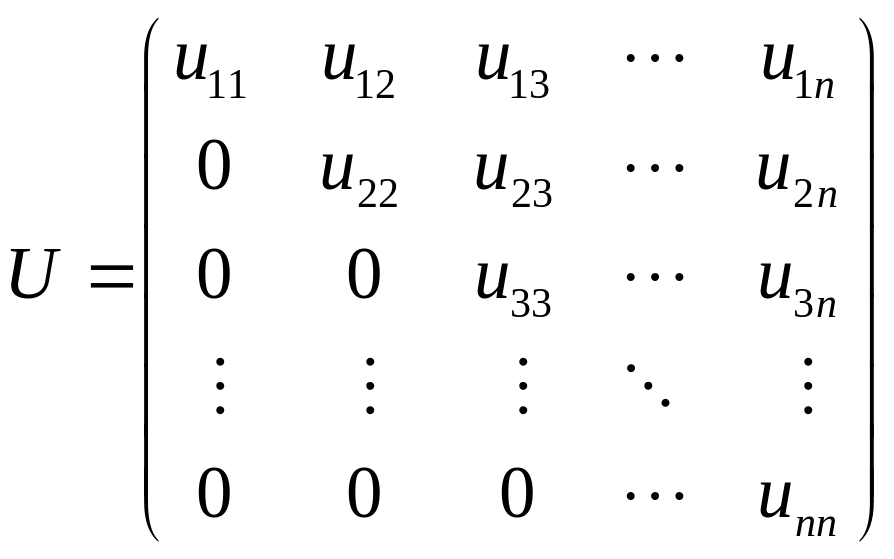 .
.
Доказано, что если главные миноры матрицы A отличны от нуля, то разложение всегда возможно и единственно.
При наличии
LU-разложения
решение системы
сводится к решению двух систем с
треугольной матрицей:
![]() .
Первая система имеет вид:
.
Первая система имеет вид:
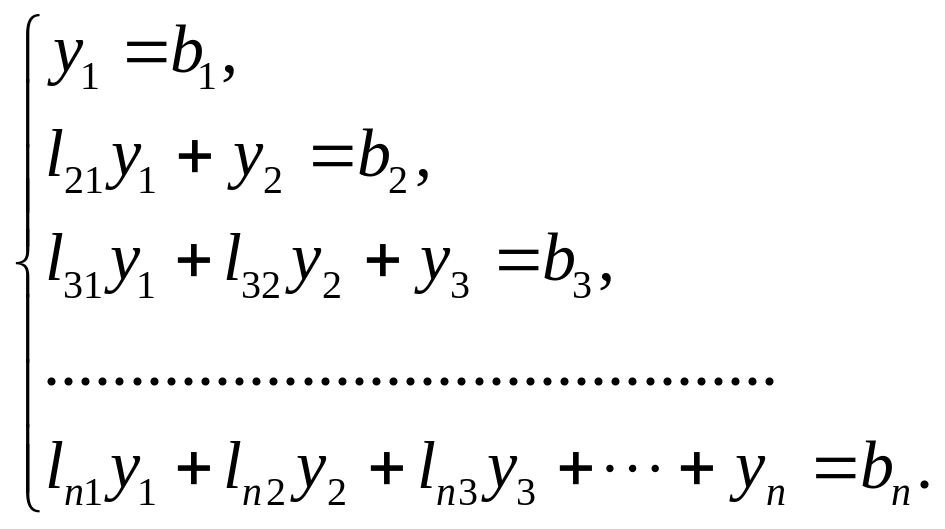
Из первого уравнения
находим
![]() ,
из второго –
,
из второго –
![]() ,
и т.д. Запишем общую формулу:
,
и т.д. Запишем общую формулу:
![]() .
.
Затем составляется
система
![]() :
:
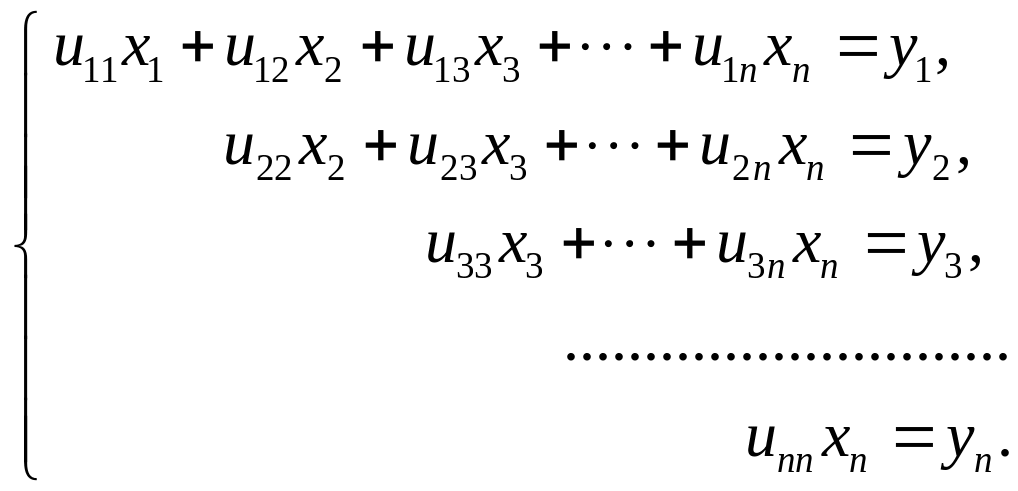
Из последнего
уравнения этой системы найдем
![]() ,
из предпоследнего –
,
из предпоследнего –
![]() ,
и т.д. Получим формулу для решения системы
,
и т.д. Получим формулу для решения системы
![]() :
:
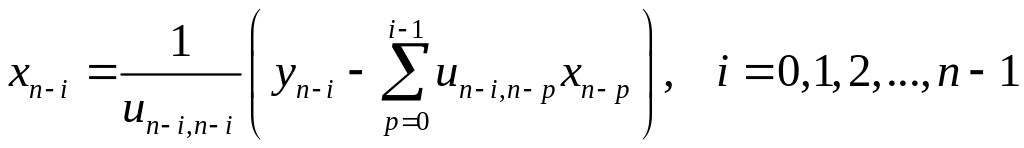 .
.
Для построения LU-разложения матрицы A создаются последовательно матрицы , где
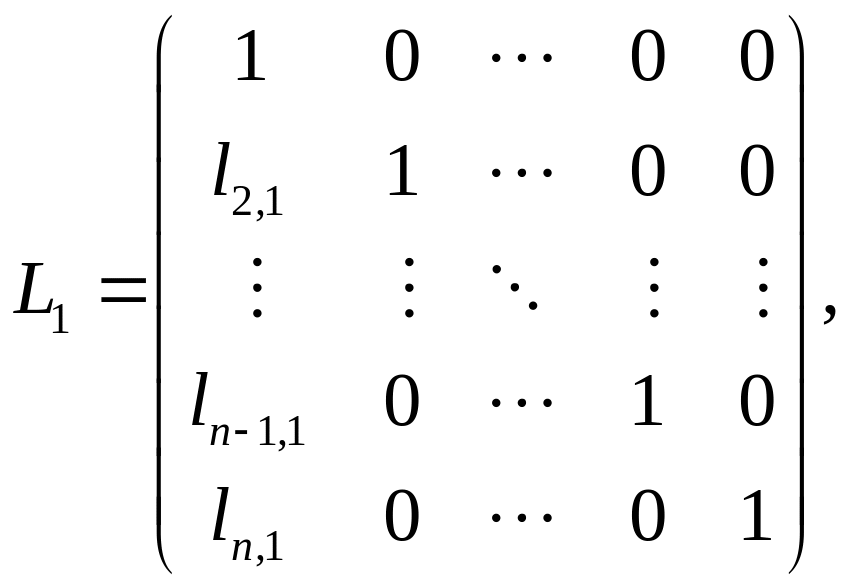
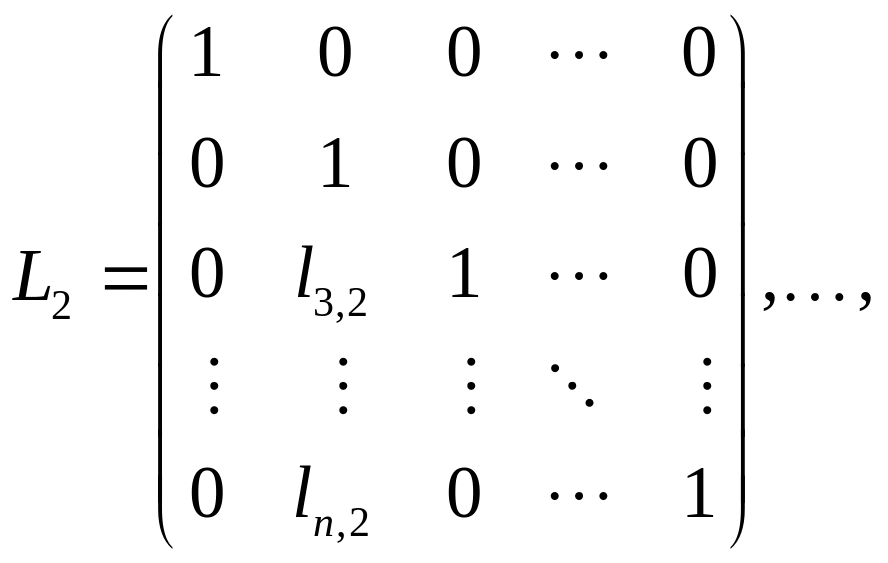
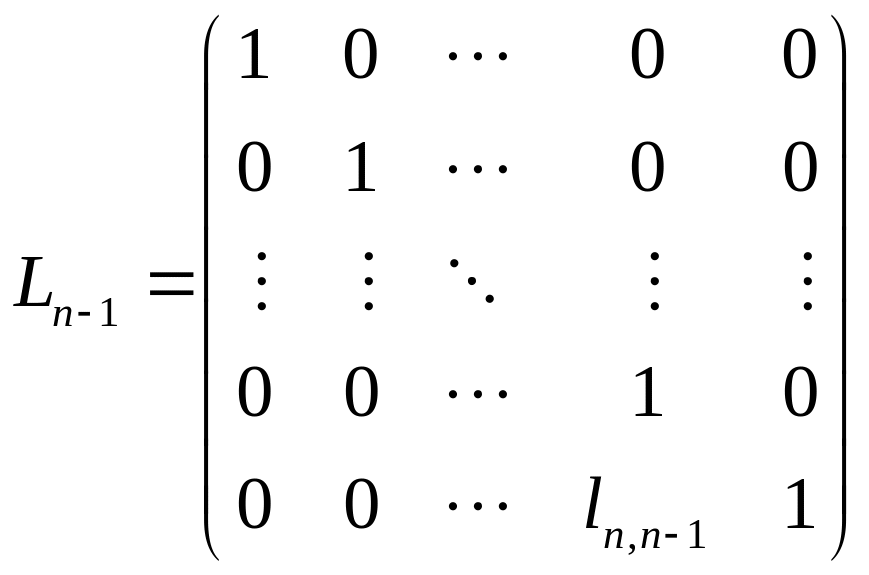
и вычисляются
матрицы
![]() .
Легко проверить, что умножение произвольной
матрицы М
порядка n
на
.
Легко проверить, что умножение произвольной
матрицы М
порядка n
на
![]() слева означает, что к строке с номером
k,
слева означает, что к строке с номером
k,
![]() ,
прибавляется строка с номером j,
умноженная на
,
прибавляется строка с номером j,
умноженная на
![]() .
Умножая матрицу
на
.
Умножая матрицу
на
![]() мы добиваемся, чтобы в j-ом
столбце матрицы
мы добиваемся, чтобы в j-ом
столбце матрицы
![]() под диагональю стояли нули. Для этого
берем
под диагональю стояли нули. Для этого
берем
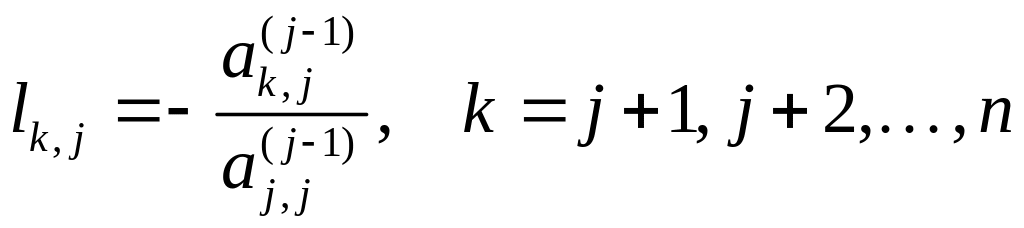 .
.
Последняя матрица
![]() будет верхней треугольной. Она выражается
через исходную матрицу
будет верхней треугольной. Она выражается
через исходную матрицу
![]() .
Пусть
.
Пусть
![]() .
Тогда
.
Тогда
![]() ,
откуда
,
откуда
![]() .
Пусть
.
Пусть
![]() ,
,
![]() .
Так как произведение нижних треугольных
матриц дает нижнюю треугольную матрицу
и обратная к нижней треугольной матрице
будет нижней треугольной, то матрица L
– нижняя треугольная. Нужное разложение
.
Так как произведение нижних треугольных
матриц дает нижнюю треугольную матрицу
и обратная к нижней треугольной матрице
будет нижней треугольной, то матрица L
– нижняя треугольная. Нужное разложение
![]() получено.
получено.
Основное преимущество метода LU-разложение заключается в том, что столбец свободных членов при решении системы линейных алгебраических уравнений используется только на заключительном этапе, а наиболее трудоемкие операции по вычислению матриц L и U не требуют знания вектора свободных членов b. Таким образом, если решается серия СЛАУ (систем линейных алгебраических уравнений) с одной и той же матрицей коэффициентов A, но разными правыми частями b, то очень выгодно один раз вычислить LU-разложение матрицы A, а уже за тем решать конкретные системы, меняя столбец свободных членов.
Если матрица A СЛАУ содержит много нулей, то использование LU-разложения может существенно сократить объем вычислений. Можно проверить, что если какая-то строка матрицы A до первого ненулевого элемента содержит m нулей, то та же строка в матрице L будет содержать в начале m нулей. Если какой-то столбец в матрице A содержит до первого ненулевого элемента p нулей, то в матрице U этот столбец в своем начале будет иметь p нулей.
Но наряду с
достоинствами метод LU-разложения
имеет и недостатки. Алгоритм LU-разложения
может остановиться даже при невырожденной
матрице A
из-за деления на нуль, если
![]() .
При ненулевом, но малом значении
.
При ненулевом, но малом значении
![]() ошибки
округлений в результате деления на
могут сильно возрастать и искажать
получаемое решение.
ошибки
округлений в результате деления на
могут сильно возрастать и искажать
получаемое решение.
Лабораторная работа №1
Цель работы:
знакомство с алгоритмом LU-разложения матрицы коэффициентов;
применение метода LU-разложения к решению систем линейных уравнений;
использование возможностей системы MATHCAD для выполнения LU-разложения.
Постановка задачи
Найти решение системы
линейных уравнений
![]() с
помощью метода LU-разложения,
где
с
помощью метода LU-разложения,
где
 – невырожденная матрица коэффициентов
размера
– невырожденная матрица коэффициентов
размера
![]() ,
,
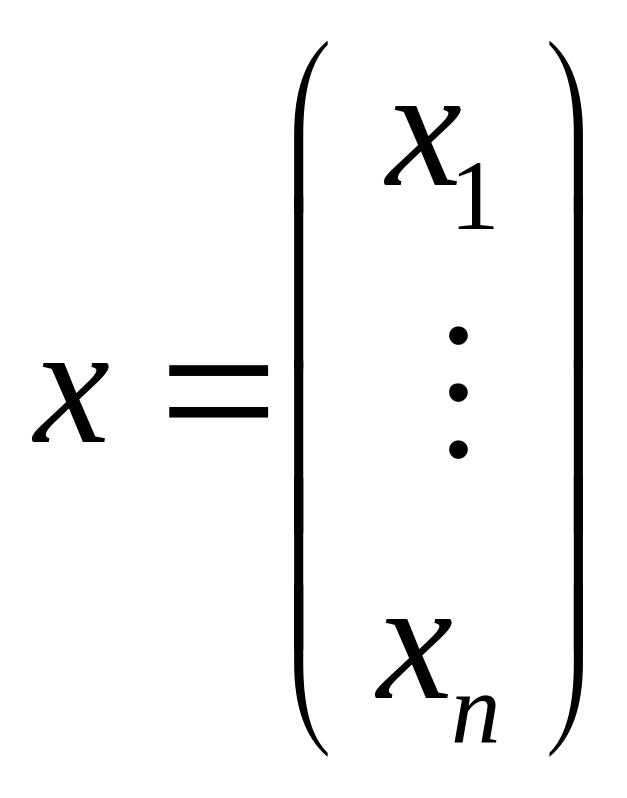 ,
,
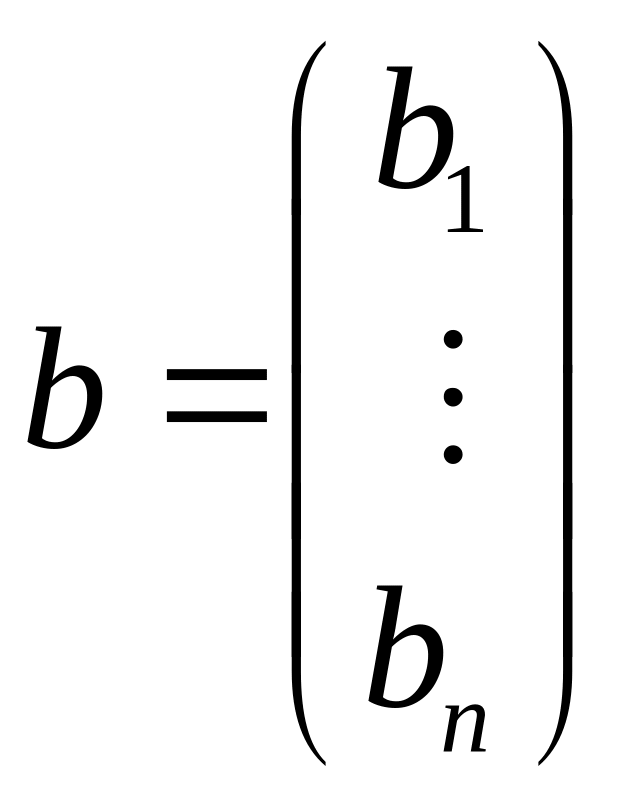 – столбец неизвестных и столбец свободных
членов соответственно.
– столбец неизвестных и столбец свободных
членов соответственно.
Ход лабораторной работы:
Ввести матрицу коэффициентов A (n×n) и столбец свободных членов b (см. задания для самостоятельной работы).
Последовательно создать матрицы и вычислить матрицы
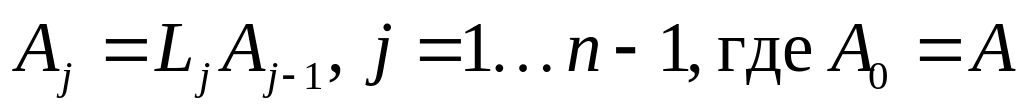 .
Элементы матриц
находятся по формулам:
.
Элементы матриц
находятся по формулам:
 ;
;
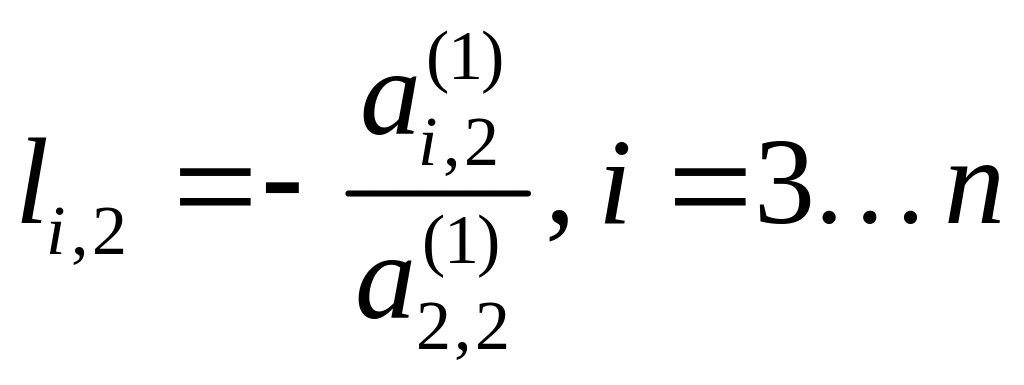 ;
…;
;
…;
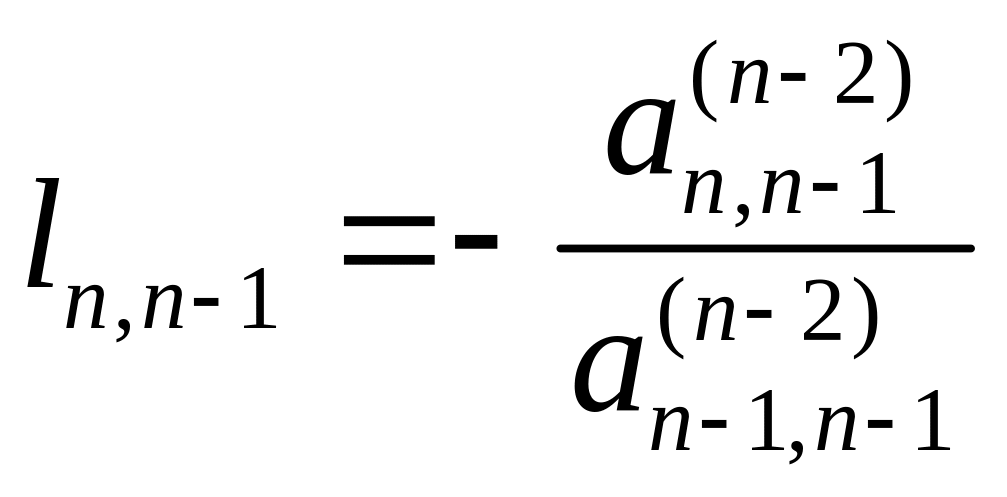 ,
где верхний индекс j
элемента
,
где верхний индекс j
элемента
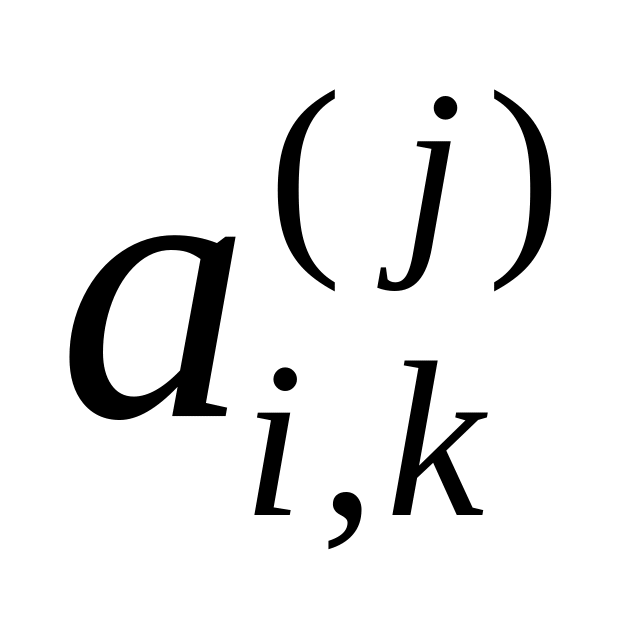 –
индекс матрицы
,
а нижние индексы
i,k
–
номер строки и номер столбца соответственно.
–
индекс матрицы
,
а нижние индексы
i,k
–
номер строки и номер столбца соответственно.Переобозначить .
Найти матрицу
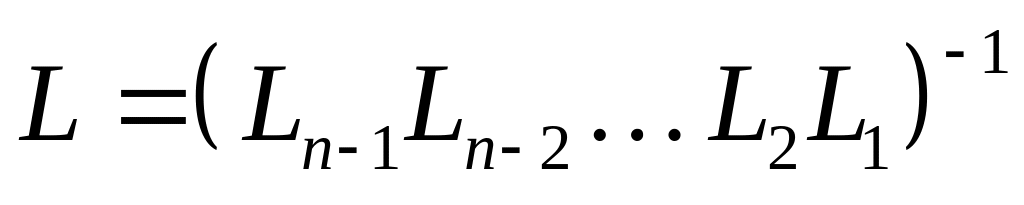 .
Заметим, что в действительности обратную
матрицу вычислять не приходится.
По правилу обращения произведения
получим
.
Заметим, что в действительности обратную
матрицу вычислять не приходится.
По правилу обращения произведения
получим
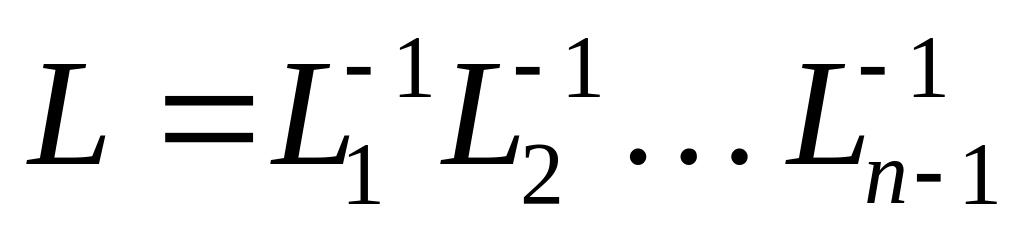 .
Легко проверяется,
что
.
Легко проверяется,
что
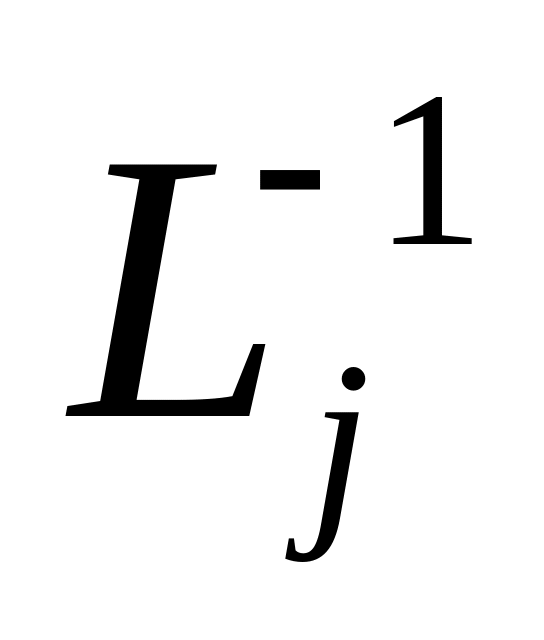 получается из
сменой
знака у ненулевых элементов j-o
столбца, стоящих ниже диагонали. По
смыслу умножения на матрицу вида
получим, что при вычислении произведения
получается из
сменой
знака у ненулевых элементов j-o
столбца, стоящих ниже диагонали. По
смыслу умножения на матрицу вида
получим, что при вычислении произведения
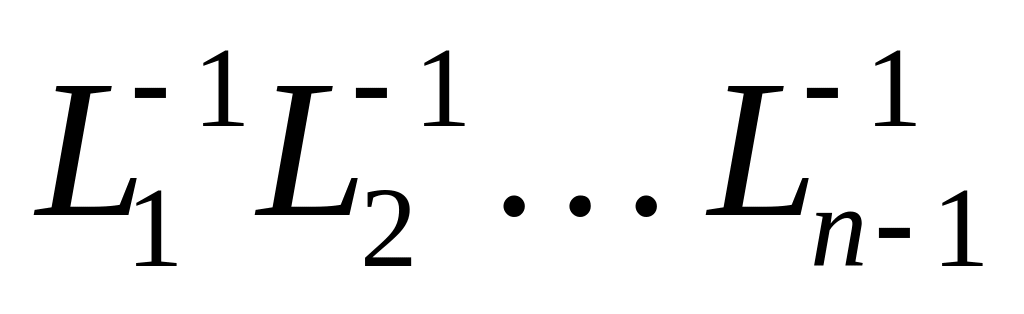 ненулевые элементы матрицы
дописываются в столбец j
матрицы L
ниже диагонали.
В результате получается матрица
ненулевые элементы матрицы
дописываются в столбец j
матрицы L
ниже диагонали.
В результате получается матрица
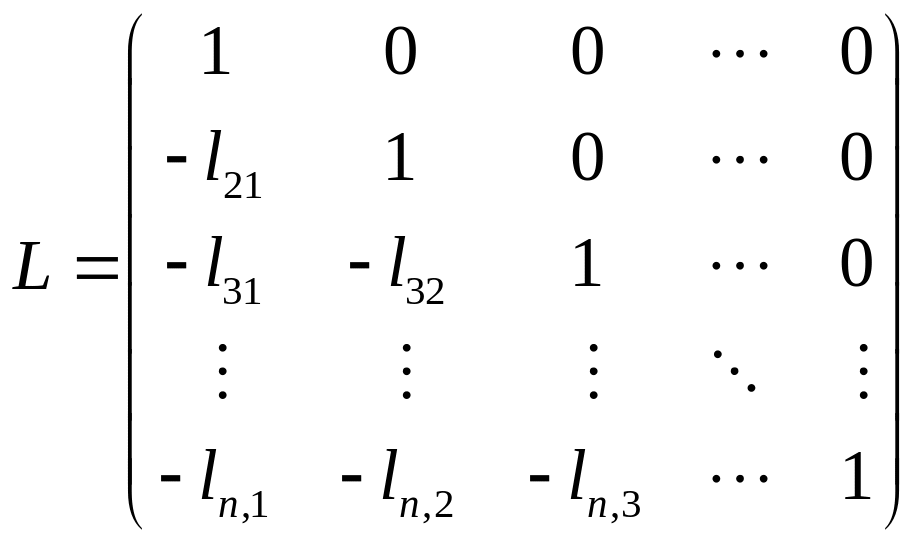 .
.Найти решение системы
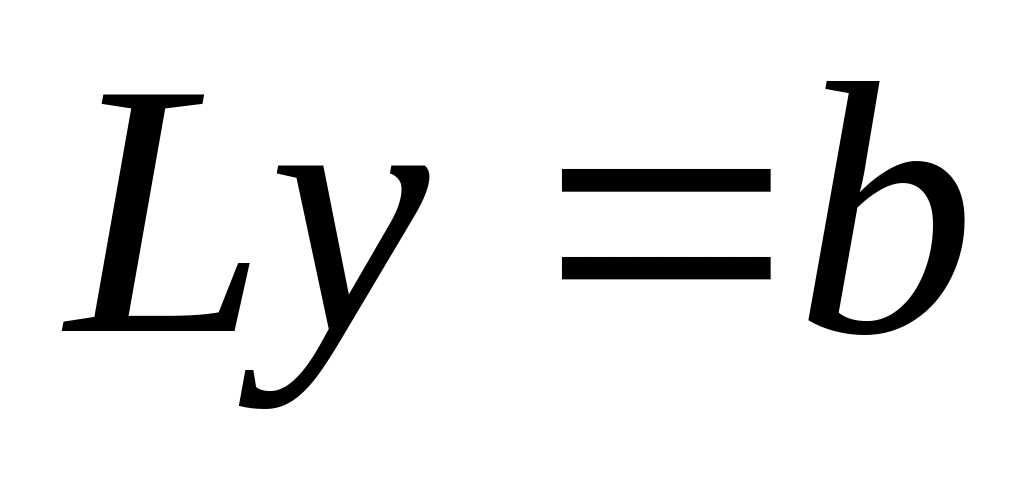 .
.Найти решение системы , записать решение исходной системы линейных уравнений.
Выполнить проверку.
1) Для проверки разложения вычислить произведение матриц LU, сравнить с исходной матрицей A.
2) Для
проверки решения посмотреть, выполняется
ли равенство
![]() .
.
Пример
Найти решение системы
линейных уравнений
,
где
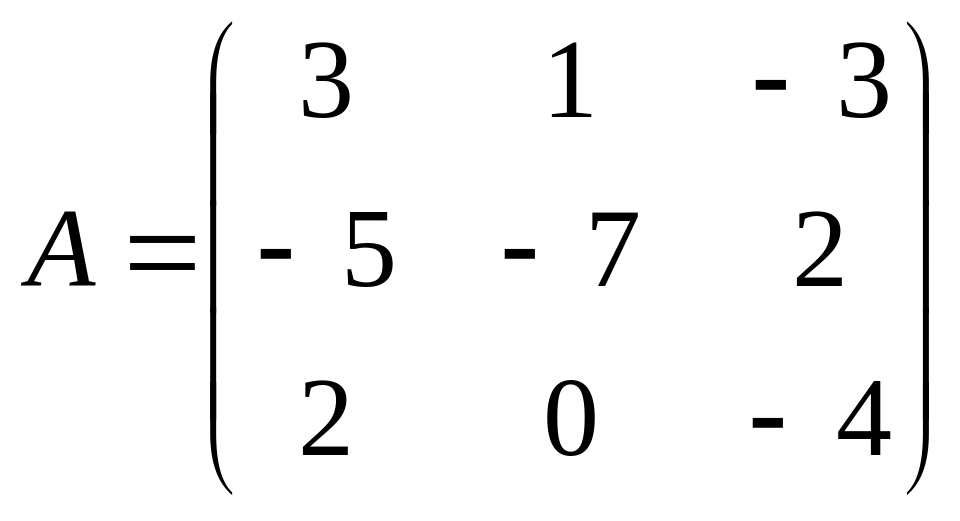 ,
,
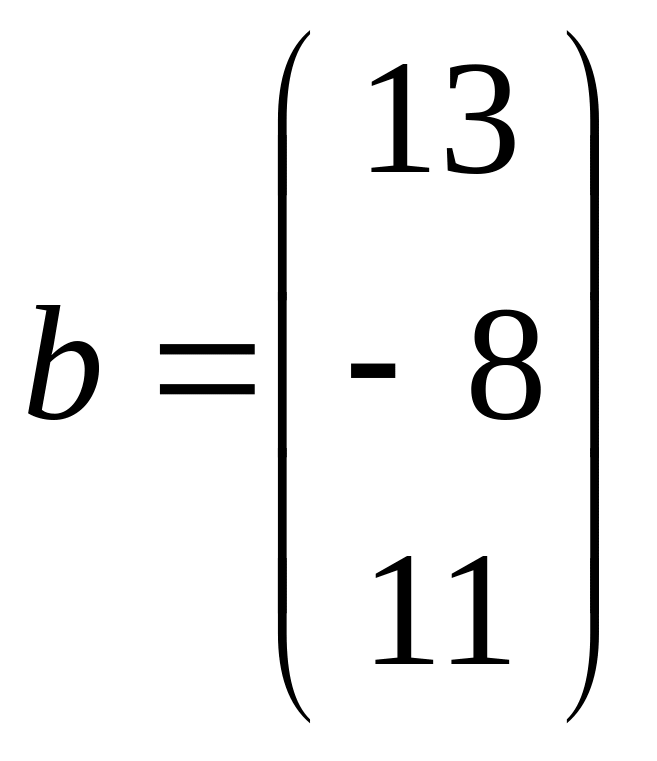 .
.
Получим LU-разложение матрицы коэффициентов.
Создаем единичную
матрицу
Задаем цикл («..» ставится при нажатии «;»):
Находим коэффициенты
|
Находим матрицу
Заметим,
что произведение матриц порядка n
требует порядка n3
действий. Оптимальнее, вместо вычисления
произведения, присвоить элементам
матрицы те значения, которые не
изменяются. Или же новую матрицу можно
не создавать, а изменять исходную.
Матрица
|
Аналогично находим матрицы L2 и A2:
|
|
Создаем матрицу L:
|
Получили матрицу U:
Разложение найдено верно, так как
|
Находим решение
системы
|
Находим решение
системы
|
Решение найдено верно, так как
|

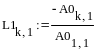
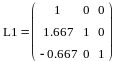
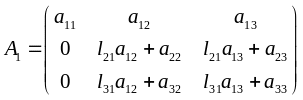 .
При большом n
будет
выполнено всего порядка n2
действий:
.
При большом n
будет
выполнено всего порядка n2
действий: