Аналитический способ нахождения экстремума.

Первые из них требуют знания производной данного уравнения с последующим нахождением ее корня – точки, в которой производная превращается в нуль, является экстремумом функции. Исключениями могут быть функции с перегибами, но для них имеет место сохранение знака производной до и после точки с нулевым значением.

Численные методы нахождения экстремума.

Численные методы позволяют находить экстремумы для любых уравнений с заданной точностью, они не требую вычисления производных и позволяют находить экстремумы, которые локализованы в определенном интервале, но они требуют большого объема вычислений. Развитие вычислительной техники позволило в настоящее время широко использовать последние методы.

У

Рис.2 Локализация экстремума функции

равнения могут содержать несколько экстремальных точек, которые должны быть локализованы интервалами поиска. Ясно, что в точке экстремума производная превращается в нуль, а слева и справа от нее производные имеют различные знаки. Пользуясь этими условиями, мы может локализовать все возможные экстремумы функции.

Как обычно реализуются численные методы поиска экстремума, рассмотрим на графике, показанном на (рис.2). Задаем интервал поиска от Х_лев до Х_пр, содержащий искомую точку экстремума и начинаем его уменьшать. Но нам надо знать в каком из новых интервалов находится экстремум. Для этого мы вычисляем не одно, а два значения функции и принимаем, что нужный нам интервал находится вокруг большей из этих точек (см. точка Х₁ рис.2), т.е. он должен быть взят от границы (Х_лев) через максимальную точку (Х₁) до второй вычисленной точки (Х₂). Интервал от Х₂ до Х_пр мы отбрасываем. Данную процедуру повторяем пока расстояние между Х_пр и Х_лев не станет меньше заданной погрешности вычисления. Ответом будет одна из двух средних точек, имеющая максимальное значение. Остается последний вопрос? Как выбирать точки для вычисления новых значений. Желательно чтобы на каждом следующем шаге нам надо было бы вычислять только одно значение функции. Для этого предлагаются два метода – золотого сечения и чисел Фибоначчи.

Т

Рис.4. Алгоритм метода итераций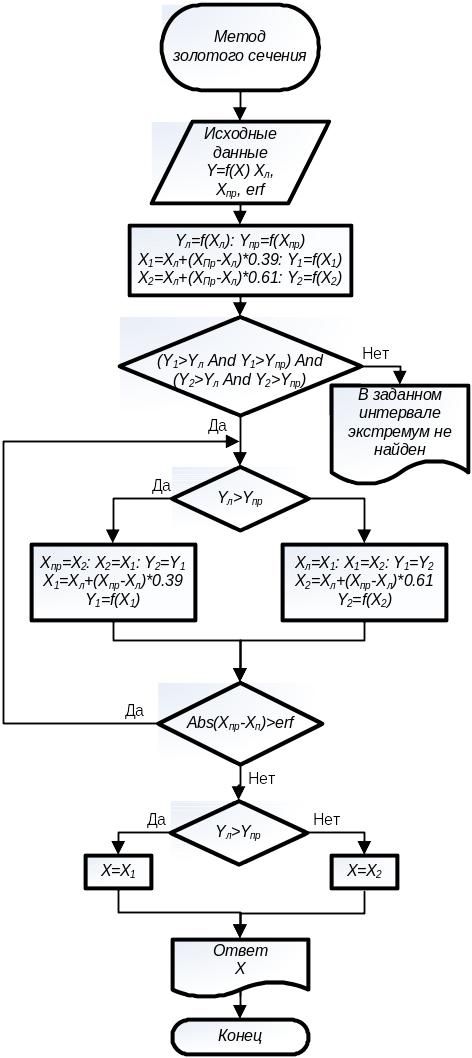

еперь возникает вопрос – можно ли совместить алгоритмы поиска максимума как мы только, что рассмотрели с поиском минимума. Если мы посмотрим на график (рис.1.) то можем сделать заключение, что любой минимум мы можем превратить в максимум функции ее умножением на -1. Следовательно, для реализации поиска максимума или минимума функции мы может использовать одну программу, но при вычислении функции нам надо умножать результат на соответствующий множитель: 1 для поиска максимума и (–1) для поиска минимума.

Алгоритмы методов

Рассмотрим алгоритмы численных методов нахождения экстремумов уравнения. Среди них более популярными является:

Метод золотого сечения

М

Рис.3 Графическое представление золотого сечения

етод золотого сечения – предполагает деление начального отрезка, где локализован экстремум функции в отношение: А:В = В:С (рис.3.) В результате, когда мы отбрасываем отрезок на одной из границ, нам надо построить только одну точку (Х₁ или Х₂). Для вычисления координат этих точек обычно используется соотношение золотого сечения – . Алгоритм метода представлен на рис. 4. Рассмотрим его более подробно. После ввода данных выполняется проверка наличия экстремума внутри интервала, если он имеется, то вычисления продолжаются, иначе выводится сообщении об его наличии в заданном интервале. Так как значения Y₁ и Y₂ нам уже известны, то мы просто проверяем какое из этих двух значений больше и на основании этого отбрасываем один из интервалов слева или справа. Надо отметить, что в отличии от методов поиска корней нам надо было переопределить только одну точку, то здесь надо переопределять две точки, что требует обязательного сохранения порядка операций, которые указаны в алгоритме. Если мы например сначала переопределим Х₁=Х₂, а потом выполним приравнивание Х_л=Х₁, то в результате обе точку получат значения Х₁, что является ошибкой.

После завершения поиска по достижению разности Х_пр-Х_л меньше ошибки erf нам надо вывести результат решения, который должен соответствовать наибольшему значению из Х₁ и Х₂