Реализация решений типовыми командами Excel

Если функции, корни которых должны быть определены, несложные, то решения могут быть получены и стандартными средствами Excel.

Т

Рис.15. Окно «Подбор параметра»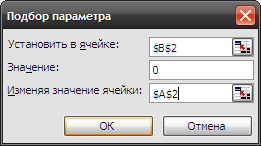

ак нахождения корня однопараметрического уравнения может быть выполнено средствами команды Сервис – Подбор параметра. Для реализации такого решения надо на листе в одну ячейку ввести начальное приближение аргумента функции для поиска ее корня и в соседнюю соответственно саму функцию. Затем вызвать окно команды Подбор параметра (рис. 15) и ввести в его параметры необходимые данные:

• «Установить в ячейке:» – указать адрес ячейки с функцией;

• «Значение» – число равное 0;

• «Изменяя значение ячейки:» – указать адрес ячейки с аргументом функции;

• нажать «Ok» для выполнения подбора результата.

Если уравнение имеет несколько корней, то надо выполнить вначале его анализ и выбрать наилучшее приближение.

Для решения многопараметрических задач можно использовать стандартную надстройку «Поиск решения». При реализации данного решения в качестве целевой ячейки используется ячейка с функцией, ее значение должно в конце расчета равняться 0, а изменяемыми ячейками должны стать ячейки с аргументами. Однако надо помнить, что данное решение не всегда будет корректным и подбор начальных условий может быть сильно затруднен.

Примеры решения типовых задач

Данные решения могут быть реализованы в следующих решениях типовых задач химической технологии:

• расчеты материального баланса процессов;

• расчеты в задачах формальной кинетики.

Рассмотрим решения данных задач с использованием созданных выше функций. Необходимо решить следующую задачу:

Производительность установки по производству синильной кислоты – 270 кг/час.

Условия протекания реакции: Т=937С, Р=1ата, Log(К) _{при Т=937С} = 1,6141.

Степень достижения равновесия – 0,9

Состав природного газа: метан – 99,0%

этан – 1,0%

Концентрация NH₃ – 100%

Мольное соотношение СН₄:NH₃ = 1 : 1,2

Реакция: CH₄ + NH₃ ↔ HCN + 3H₂

В результате решения получаем уравнение третьей степени с неизвестным количеством поданного CH₄ – А:

Записываем данную функцию либо как функцию пользователя или записываем ее как формулу на листе Excel

Заключение

В результате выполнения работы были разработаны программы для нахождения корней уравнения, которые могут быть использованы в следующих работах и курсах, а так же при выполнении расчетов во время курсовых и дипломных работ.

Самостоятельная работа

2. На отдельных листах книги Excel реализуйте методы итераций и касательных для следующих функций:

3. Разработать фрагмент программы «FDihot2» на случай отсутствия корня по время поиска необходимого интервала?

Контрольные вопросы

4. Что такое корень уравнения?

5. Как реализуется алгоритм итераций?

6. Опишите алгоритм касательных для поиска корня.

7. Как реализуется метод деления отрезка пополам.

Лабораторная работа № 3

Нахождение экстремумов уравнения. Введение

Экстремумы уравнений, их определение.

Э

Рис.1 Экстремум уравнения

кстремумами уравнения являются его точки, в которых значения функции принимают максимальные или минимальные значения. Экстремумы могут быть локальными (их может быть несколько) и глобальным (их не более двух – один их них максимум, а другой минимум), они является самым большим среди максимумов или минимумов функции. Примеры экстремумов показаны на рис.1. Здесь имеются два минимума (Х_э1 и Х_э3) причем первый из них локальный, а второй глобальный. Если предположить что дальше минимумов больше не будет. Х_э2 является максимумом функции.

Для нахождения экстремумов существуют аналитические и приближенные методы.