Метод деления отрезка пополам

Метод деления отрезка пополам (дихотомии) – задается интервал, в котором имеется корень (проверка наличия корня внутри интервала выполняется вычислением значений функции на его границах с последующей проверкой этих значений на разные знаки через операцию умножения – если произведение меньше нуль, то знаки на границах интервала разные). Затем интервал разбивается на два и выбирается тот, в котором остался корень. Процедура повторяется, пока интервал не станет меньше погрешности erf. Алгоритм метода показан на рис.7. Обычно всегда проверяется левый интервал, а после проверки выбирается необходимый. Ответом является середина последнего интервала. Для ускорения работы алгоритма можно проверять и попадание в сам корень, в этом случае произведение становится равным нулю, а корень оказывается на одной из границ интервала. Разберем данную процедуру на примере:

• задаем уравнение Y=f(X), погрешность вычисления и левую границу Х_л;

• з

  

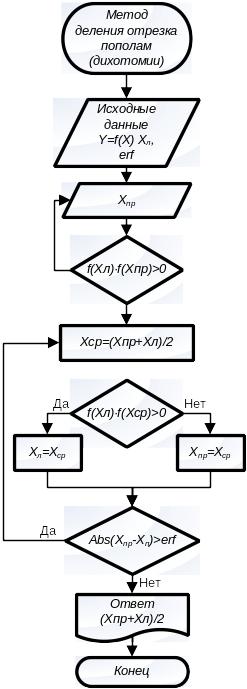
  Рис.7. Алгоритм метода деления отрезка пополам (дихотомии)

  адаем правую границу Х_пр и проверяем произведения f(X_л)·f(X_пр). Если значение больше нуля повторяем ввод правой границы, если меньше переходим к реализации алгоритма, а если равен нулю, определяем границу, где найден корень;

• находим середину интервала Х_ср=(Х_пр+Х_л)/2 и проверяем значение произведения для левой половины f(X_л)·f(X_ср). Если значение равно нулю, то корень в средней точке, если значение меньше нулю, то левый интервал содержит корень и правую часть можно отбросить приравняв Х_пр= X_ср иначе корень находится в правой части и отбрасываем левую Х_л= X_ср;

• процедуру повторяем, пока (Х_пр-Х_л)>erf. Ответом является среднее значение найденного интервала.

Реализация решений в среде Excel

Попробуем реализовать последний метод средствами листа Excel, то есть, не используя программ VBA, а потом тот же алгоритм реализуем программно средствами VBA.

Примем следующий алгоритм расчета – начальная строка таблицы задает исходные данные, а каждая следующая строка содержит результат очередной итерации при поиске решения.

О

Рис.8. Запрос системы безопасности

ткрываем книгу, которую создали на прошлом занятии. Так как в ней были макросы, система выдаст запрос (рис.8), в котором надо подтвердить открытие макросов щелчком на кнопке «Не отключать макросы» .Если данное окно не появляется, то это говорит о том, что система безопасности находится в состоянии «Высокая». Чтобы перейти на уровень безопасности «Средняя» надо выполнить команду «Сервис»–«Макрос»–«Безопасность…» и на закладке «Уровень безопасности» выбрать «Средняя».

На новом листе книги «МКХТП.xls» делаем заготовку таблицы, которая нам нужна для реализации метода. Это собственно заголовок таблицы с именем метода и заголовки столбцов для каждой из точек, которые надо вычислять, а так же столбец со значениями ошибки (рис.9). Исходными данными будут значения параметра на левой и правой границах интервала. Отметим их цветом фона, чтобы помнить о необходимости ввода данных в эти ячейки.

Т

Рис. 9. Заголовок таблицы для реализации метода деления отрезка пополам

еперь начнем заполнять остальные ячейки формулами. В первую очередь вычислим значения «Y», которое будем вычислять по модельной функции, созданной на прошлом занятии «My_fun». Для этого встаем в первую ячейку столбца «Y» для левой границы, вводим «=» и вызываем мастера функций и выбираем созданную нами функцию. В ячейке должна быть получена следующая запись – =My_fun(A4). Теперь эту ячейку мы можем просто скопировать в столбцы «Y» для середины и правой границы, нажав комбинацию клавиш [Ctrl+C] или воспользовавшись командой меню или пиктограммой «Копировать». Встаем в нужные ячейки и выполняем команду «Вставить» [Ctrl+V] или через команды меню либо кнопками панели инструментов. Копирование ячейки можно выполнить и мышкой, для этого надо выделить нужную ячейку, потом захватить ее за границу (при этом курсор мышки измениться на стрелку с меленькими стрелками на конце) и нажать клавишу Ctrl (рядом с курсором появится значок плюс) теперь можно перетащить ячейку туда, куда надо выполнить копирование. Операция может быть сразу же повторена уже с новой ячейкой.

Так как в ячейке столбца «Х» для середины нет данных, то ответ будет вычислен от нулевого значения, что даст для нашей функции ошибку. Чтобы от нее избавиться вычислим данное значение по следующей формуле – =(A4+E4)/2, где А4 и Е4 адреса ячеек столбцов «Х» левой и правой границ. Остается только вычислить значение ошибки в последнем столбце таблицы в виде следующего выражения – =ABS(E4-A4).

Теперь остается ввести две последние формулы для вычисления новых значений Х на границах отрезка для следующей итерации. Левая граница вычисляется по выражении – =ЕСЛИ(B4*D4<0;A4;C4), где В4 и D4 указывают на значения функции «Y» для левой и средней точек, а А4 и С4 – значения параметров «Х» для тех же точек. Выражение для правой границы так же вычисляется от произведения левой и средней точек, так как иначе могут возникнуть противоречия в решении при попадании средней точки в корень (Y=0). Выражение «Х» для правой границы имеет вид – =ЕСЛИ(B4*D4<0;C4;E4).

Остальные формулы второй строки можно просто скопировать с первой строки. Для этого выделяем сначала три ячейка от «Y» для левой точки до «Y» в середине и растягиваем за угол на следующую строку. Повторяем эту же операцию и для двух последних ячеек первой строки («Y» для правой точки и ошибку). Теперь строка для итерации готова и ее можно просто копировать нужное число раз, пока значение ошибки не станет меньше заданного значения. При ошибке меньше 0,01 получаем результат, показанный на рис.10.

Как видим по результатам на каждой итерации ошибка уменьшается наполовину.

Т

Рис.10. Результат поиска корня модельной функции.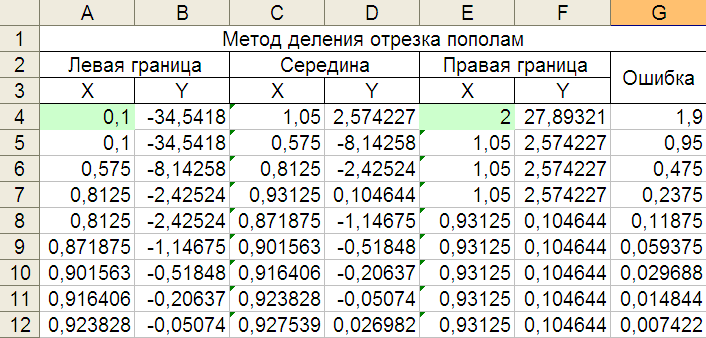

еперь реализуем эту же задачу еще двумя способами:

• Построим макрокоманду, которая будет строить решение задачи непосредственно на листе для заданных там же условий. Например, мы указываем начальные точки и записываем в определенную ячейку функцию, которую нам нужно решить. Этот подход позволяет наглядно показать метод решения задачи и построить графики приближения к решению на каждом шаге;

• Создадим непосредственно функцию пользователя, которая сразу же возвращает точку корня, что обычно и нужно при решении прикладных задач.

С

Рис. 11. Образец заготовки для макроса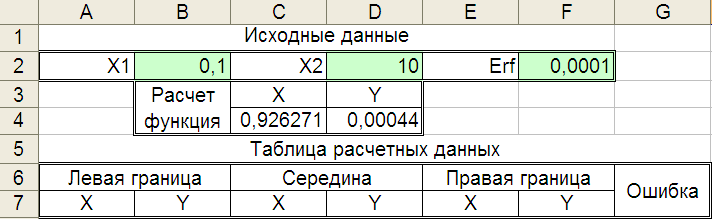

начала разберем первую задачу, которая должна нам построить таблицу данных, подобную той, что мы только, что получили. Вначале определим структуру листа, где будет реализовываться макрос. Для этого подготовим лист следующим образом (рис.11). Переименуем лист в «МДОП1». На нем сделаем заголовок и определим ячейки, которые будут использоваться для ввода данных (отмечены светло-зеленым цветом). Ниже, под заголовками «Х» и «Y» зарезервируем ячейку для текущего значения «Х» и ячейку, куда собственно запишем саму функцию «Y». Чтобы сравнить результаты расчетов, в качестве функции используем «My_fun».

Переходим в VBA и пишем сам макрос. Сначала создаем заготовку для подпрограммы (макроса) с именем «Dihot1». Чтобы не создавать много программ в одном модуле, предварительно создаем еще один «Module2», и уже в него вставить сам макрос. Теперь надо считать с листа границы области поиска корня и точность решения «erf». Это реализуется следующим кодом:

ThisWorkbook.Sheets("МДОП1").Activate

ThisWorkbook.Sheets("МДОП1").Cells(2, 1).Select

X1 = ActiveCell.Offset(0, 1)

X2 = ActiveCell.Offset(0, 3)

Erf = ActiveCell.Offset(0, 5)

Разберем назначение каждого из операторов. В первой и второй строках делаем активным нужный нам лист и устанавливаем курсор ввода на первую ячейку второй строки листа «МДОП1». Это нам надо для определения точки, откуда мы будем иметь доступ к остальным ячейкам листа. Следующие три строку считывают данные их ячеек листа. Данный оператор находит ячейку относительно активной ячейки (которая была установлена вторым оператором) смещением на указанное число строк и столбцов соответственно. Так для левой границы от ячейки (2,1) надо переместиться на столбец вправо (+1). Знаки «+» можно опустить. Теперь вычисляем значения нашей функции в заданной точке.

ActiveCell.Offset(2, 2) = X1

Y1 = ActiveCell.Offset(2, 3)

If Y1 = 0 Then

MsgBox "Корень в точке " & Str(X1)

Exit Sub

End If

Первым оператором переносим значение «Х1» в ячейку для текущего «Х». Excel автоматически пересчитывает значение функции в ячейке «Y». Следующим оператором получаем значение функции в «Y1». Теперь надо проверить, не является ли данная точка корнем уравнения. Используем оператор «If» для проверки равенства значения «Y1» нуль. Если это так, то выводим окно с информацией, что эта точка является корнем функции с помощью оператора «MsgBox» и выходим из подпрограммы. Подобный фрагмент пишем и для правой границы с данными по «Х2» и «Y2», который показан ниже:

ActiveCell.Offset(3, 2) = X2

Y2 = ActiveCell.Offset(3, 3)

If Y2 = 0 Then

MsgBox "Корень в точке " & Str(X2)

Exit Sub

End If

Теперь проверяем наличие корня в заданном интервале:

If Y1 * Y2 > 0 Then

MsgBox "Корня в заданном интервале нет "

Exit Sub

End If

Для построения итоговой таблицы надо определить номер строку, откуда данная таблица должна начинаться. В нашем случае это строка 8 (см. рис.10) и от активной ячейки (2,1) нам нужно смещение в 6 строк:

i = 6

Теперь реализуем сам алгоритм поиска корня. Для этого задаем цикл с пост условием:

Do

…

Loop Until Abs(X2 - X1) < Erf

Выход из цикла реализуем по условию, что разница между Х1 и Х2 по абсолютной величине меньше заданной ошибки «erf».

Внутри цикла вычисляем середину интервала Х и значение функции в этой точке. Проверяем наличие в ней корня:

X = (X1 + X2) / 2

ActiveCell.Offset(3, 2) = X

Y = ActiveCell.Offset(3, 3)

If Y = 0 Then

MsgBox "Корень в точке " & Str(X)

Exit Sub

End If

Печатаем вычисленные значения в таблицу и увеличиваем номер строки последним оператором:

ActiveCell.Offset(i, 0) = X1

ActiveCell.Offset(i, 1) = Y1

ActiveCell.Offset(i, 2) = X

ActiveCell.Offset(i, 3) = Y

ActiveCell.Offset(i, 4) = X2

ActiveCell.Offset(i, 5) = Y2

ActiveCell.Offset(i, 6) = Abs(X2 - X1)

i = i + 1

Теперь находим интервал с корнем и переопределяем границы

If Y * Y1 < 0 Then

X2 = X: Y2 = Y

Else

X1 = X: Y1 = Y

End If

После оператора завершения цикла «Loop» надо повторить операторы вычисления Х, Y и вывода результатов расчета в таблицу. В конце можно добавить вывод результата расчета в окно сообщения оператором:

MsgBox "Корень в точке " & Str(X)

Т

Рис.12. Результат работы макроса «Dihot1»

Рис.13. Окно сообщения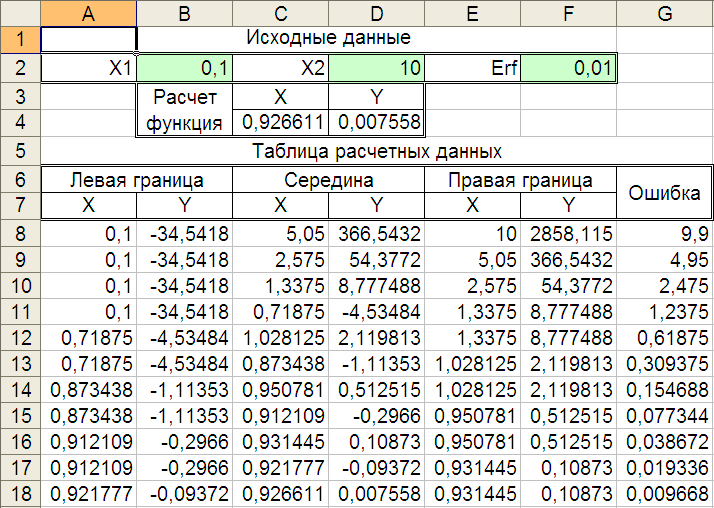

еперь надо сохранить результаты работы и перейти на лист «МДОП1», внести необходимые данные для интервала поиска и точность решения. После этого можно запустить макрос, используя комбинацию горячих клавиш [Alt+F8], выбираем «Dihot1» и нажимаем кнопку «Выполнить». В результате работы макросы мы получаем таблицу (рис.12). Окно сообщения показано на рис. 13.

Как можно оптимизировать нашу программу? Реально в ней имеются два фрагмента, которые встречаются по нескольку раз. Это вычисление значения функции для данного Х и вывод данных в таблицу. Их можно перенести в подпрограммы. Попробуем сделать соответствующие изменения.

Сначала организуем вывод данных на лист. Создадим подпрограмму (Sub) с именем «Output» и сделаем ее «Private», чтобы не видеть ее среди макросов. Перенесем в нее строки вывода расчетных данных на лист и получим следующий фрагмент программы:

Private Sub Output()

ActiveCell.Offset(i, 0) = X1

ActiveCell.Offset(i, 1) = Y1

ActiveCell.Offset(i, 2) = X

ActiveCell.Offset(i, 3) = Y

ActiveCell.Offset(i, 4) = X2

ActiveCell.Offset(i, 5) = Y2

ActiveCell.Offset(i, 6) = Abs(X2 - X1)

i = i + 1

End Sub

И заменяем эти строки в основной программе обращение к подпрограмме по ее имени «Output». Но чтобы она заработала надо обеспечить доступ к переменным Х1 и т.д. Для этого первой строкой в модуле должна быть написана следующая строка:

Public X, X12, X2, Y, Y1, Y2, i

Она определяет перечень общих переменных для всего модуля.

Теперь создадим вторую подпрограмму, но она должна возвратить в основную программу наличие корня и обеспечить выход из основной программы. Поэтому сделаем ее функцией с именем «GetY» и перенесем в нее строки заполнения данными текущего Х, считывания Y и проверки наличия корня. Так как это функция, то входным параметром будет Х, назовем этот параметр именем «ХХ». Возвращает функция значение «YY»:

Private Function GetY(XX)

ActiveCell.Offset(3, 2) = XX

YY = ActiveCell.Offset(3, 3)

If YY = 0 Then

MsgBox "Корень в точке " & Str(XX)

End If

GetY = YY

End Function

Из условия убираем выход из процедуры и переносим его дополнительной строкой в основную программу с соответствующим «Y»:

If Y1 = 0 Then Exit Sub

Окончательно программа выглядит так:

Public X, X12, X2, Y, Y1, Y2, i

Public Sub Dihot1()

ThisWorkbook.Sheets("МДОП1").Activate

ThisWorkbook.Sheets("МДОП1").Cells(2, 1).Select

X1 = ActiveCell.Offset(0, 1)

X2 = ActiveCell.Offset(0, 3)

Erf = ActiveCell.Offset(0, 5)

Y1 = GetY(X1)

If Y1 = 0 Then Exit Sub

Y2 = GetY(X2)

If Y2 = 0 Then Exit Sub

If Y1 * Y2 > 0 Then

MsgBox "Корня в заданном интервале нет "

Exit Sub

End If

i = 6

Do

X = (X1 + X2) / 2

Y = GetY(X)

If Y = 0 Then Exit Sub

Output

If Y * Y1 < 0 Then

X2 = X: Y2 = Y

Else

X1 = X: Y1 = Y

End If

Loop Until Abs(X2 - X1) < Erf

X = (X1 + X2) / 2

Y = GetY(X)

If Y = 0 Then Exit Sub

Output

MsgBox "Корень в точке " & Str(X)

End Sub

Рассмотрим вторую задачу – получить сразу же ответ (корень уравнения), что бывает необходимо при решении больших задач, когда поиск корня является просто промежуточным решением. Сначала построим самое простое решение. Мы вводим границы интервала, ошибку решения и имя функции, корень которой мы ищем. После вычисления машина нам возвращает ответ или какое-то определенной число, говорящее нам, что корня в этом интервале нет.

Создаем новый модуль «Module3» и в нем создаем функцию «FDihot1». Функция имеет четыре формальных параметра «Х1», «Х2», «erf» и «Fn», которые записываем в заголовок функции между скобками. Ниже пишем саму программу:

Public Function FDihot1(X1, X2, Erf, Fn as String)

If Erf = 0 Then Erf = 0.01

Y1 = Application.Run(Fn,X1)

If Y1 = 0 Then

FDihot1 = X1

Exit Function

End If

Y2 = Application.Run(Fn,X2)

If Y2 = 0 Then

FDihot1 = X2

Exit Function

End If

If Y1 * Y2 < 0 Then

Do

X = (X1 + X2) / 2

Y = Application.Run(Fn,X)

If Y = 0 Then

FDihot1 = X

Exit Function

End If

If Y * Y1 < 0 Then

X2 = X

Else

X1 = X: Y1 = Y

End If

Loop Until Abs(X2 - X1) < Erf

FDihot1 = (X2 + X1) / 2

Else

FDihot1 = 7777

End If

End Function

Первая строка исключает ошибку в работе программы, когда «erf» не задано или ошибочно задано 0. Потом проверяем, нет ли корня на границах интервала. Затем проверяем, есть ли корень внутри интервала. В случае если его нет, просто выводим число 7777, иначе вычисляем сам корень.

Попробует сделать решение более универсальным, будем задавать только одну границу и точность решения. Существуют различные варианты нахождения интервала с корнем. Мы воспользуемся следующим – зададим небольшой шаг и начинаем искать интервал, удовлетворяющий нашим условиям, перемещая каждый раз обе границы. Это приводит к поиску корня в небольшом интервале, но с другой стороны поиска интервала можем быть долгим. Второй вопрос, который надо решить это направление поиска интервала. Его будем делать по следующей схеме: в начальной точке определяем значения функции и ее производной (для этого воспользуемся подпрограммой Dif_Ur, разработанной на прошлом занятии).

Для создания новой программы воспользуемся уже созданной функцией. Делам копию функции FDihot1, изменяем ее имя и все внутренние выходы на «FDihot2». Теперь внесем необходимые изменения. Заменяем строки по проверке Х2 на следующий фрагмент:

dY1 = Dif_Ur(X1, Fn))

St= IIf(Y1 > 0, IIf(dY1 > 0, -1, 1), IIf(dY1 > 0, 1, -1))

H = St * 5

Do

X2 = X1 + St * H

Y2 = Application.Run(Fn,X2)

If Y2 = 0 Then

FDihot2 = X2

Exit Function

End If

If Y1 * Y2 > 0 Then

X1 = X2: Y1 = Y2

Else

Exit Do

End If

Loop

If X1 > X2 Then

X = X1: X1 = X2: X2 = X: Y1 = Y2

End If

Определяем производную и потом направление поиска, если St<0 шаг отнимаем и наоборот. Потом в цикле «Do … Loop» находим Х2 и вычисляем значения Y2. Выполняем проверку Y2 на наличие корня. Если корня нет, то проверяем наличие корня в интервале. Если он есть выходим из цикла иначе переопределяем Х1 на Х2 и Y1 на Y2 и повторяем поиск интервала. Проверка после завершения цикла обеспечивает переопределение точек по их возрастанию Х1<Х2, что необходимо в самом алгоритме деления отрезка пополам.

В

Рис.14. Фрагмент таблицы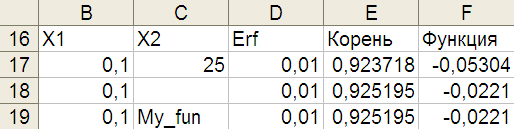

нашем решении мы использовали шаг равный 5, но в ряде случаев этот шаг может перекрыть область с двумя корнями. Для исключения данной ситуации можно еще проверять и значение производной в точке Х2 и при условии что две производные имеют разный знак, просто уменьшаем наш шаг наполовину. Хотя наилучший вариант поиска корней это на первом этапе просто локализовать все возможные корни исследуемой функции и потом уже выполнять их поиск.

Проверим работу этих функций. Перейдем на лист «МДОП» и в нижней части листа организуем следующие записи (рис.14). В ячейках под заголовками «Х1», «Х2» и «erf» вносим необходимые числа. Под заголовком «Корень» записываем две созданные функции «FDihot1» и «FDihot2» соответственно. Под заголовком «Функция» соответственно исследуемая функция «My_fun».