Алгоритмы методов

Рассмотрим алгоритмы численных методов нахождения корней уравнения. Среди них наиболее популярными являются:

Метод итераций

М

Рис.4. Алгоритм метода итераций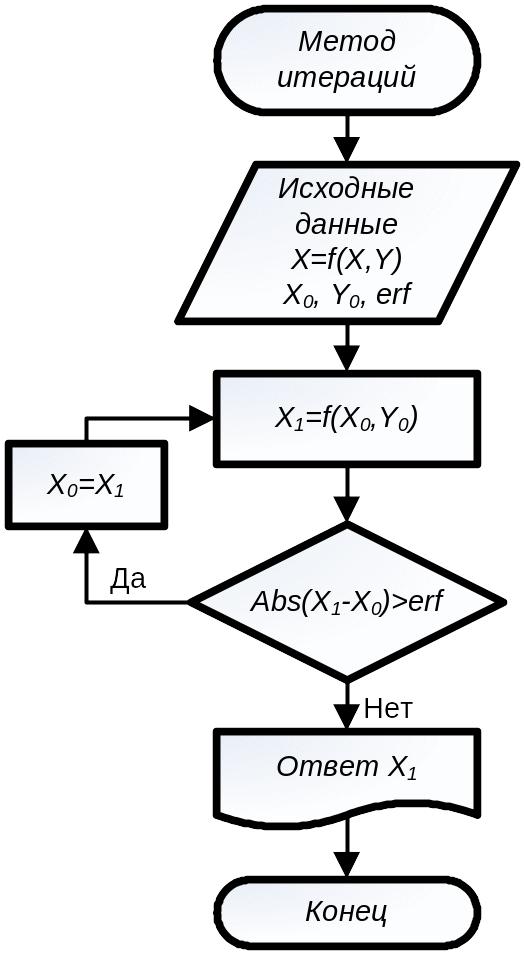

етод итераций – трансцендентное уравнение приводится к виду X=f(X,Y) затем задается начальное значение Х, через указанную зависимость находится следующее значение Х и процедура повторяется пока разница между этим значением и предыдущим не станет меньше наперед заданной величины – погрешность вычисления erf. Алгоритм решения представлен на рис.4. Рассмотрим пример:

• имеется уравнение – . Мы не может явно разделить переменные;

• преобразуем уравнение в вид – . Для этого освободим Х от степени, разделив все члены уравнении на Х². В результате получаем выражение и выделяем . Считаем, что Х справа есть начальное значение, а слева следующее приближение к корню;

• задаем начальные значения – Х=5 и Y=0, находим новое приближение и подставляем его в это выражение снова. Повторяем процедуру, пока разница между двумя Х не станет меньше erf=1E-5.

Метод касательных(хорд)

М

Рис.5 Графическая реализация метода касательных (хорд)

етод касательных (хорд) – уравнение в заданной точке рассматривается как линейное, соответствующее касательной к заданному уравнению в этой точке. По ней находится корень (точка пересечения касательной с осью Х), который является следующим приближением к решению. Графическое представление метода показано на рис.5. Метод очень чувствителен к выбору начальной точки. Касательные можно заменять хордами, проведенными через две точки, равно отстоящие от заданной, как при вычислении производной (см. выше). Алгоритм метода показан на рис.7. Рассмотрим пример реализации решения:

• если мы имеем уравнение с известным алгебраическим уравнением производной, то задача сводится лишь к нахождению точки пересечения линии с осью Х (об этом чуть ниже)

• е

  

  Рис.6. Алгоритм метода касательных (хорд)

  сли алгебраического выражения производной нет, то надо построить уравнение прямой одним из двух методов – по углу наклона прямой и точке, через которую это уравнение проходит или по двум точкам, через которые это уравнение проходит. Реально угол наклона это собственно и есть первая производная уравнения в данной точке. Её мы можем найти по показанному выше алгоритму. Для второго варианта можно воспользоваться только двумя точками, которые мы имеем для вычисления производной;

• теперь вспомним процедуры вычисления неизвестных коэффициентов линейного уравнения вида Y=a+b·X на основании имеющихся данных:

  • при известном угле наклона b и на основании известных координат заданной точки (X₀, Y₀) находим a по следующей формуле ;

  • по двум точкам (X_+, Y_+) и (X_-, Y_-) находим и , используя одну их имеющихся точек.

• имея уравнение прямой, находим точку пересечения его с осью Х.

Принимаем, что Y=0 и вычисляем . Это значение является следующим приближением к корню. Повторяем процедуру, пока разница между двумя последними Х не станет меньше erf=1E-5.

При использовании метода хорд надо следить, чтобы две выбранные точки лежали с одной стороны от корня, то есть имели одинаковый знак.