Работа в vba

Вспомним приемы программирования в среде VBA for Excel, для этого построим две функции, которые мы будем использовать дальше.

Первая из них – это функция пользователя, которая должна содержать нашу модель для исследования, чтобы ее каждый раз не набирать средствами Excel. В нашем случае это следующее уравнение – Y=3·(Х-0,2)³+15·Ln(X)

Открываем VBA, используя комбинацию клавиш «Alt+F11» или непосредственно вызывая команду из меню MS Excel – «Сервис»–«Макрос»–«Редактор Visual Basic». Вставляем в наш проект модуль командой «Insert»–«Module». В списке проекта появляется новый объект «Module1».

В

Рис.14. Окно создания процедуры.

стаем курсором мышки в окно модуля и вставляем в него процедуру командой «Insert»–«Procedure». В появившемся окне создания процедуры (Рис.14) в поле «Name» пишем имя «My_fun». Имя не должно начинаться с цифры и содержать пробелы, если надо разделить символы в имени процедуры надо использовать символ подчеркивания «_». Если функция должна иметь формальные параметры, которые она принимает при вызове, то их записываем уже в модуле при создании самого кода. Потом выбираем «Type» функции – (Function) и нажимаем кнопку «Ok». В модуле появляется заготовка функции, которая содержит строку с ее названием и последнюю строку со служебным словом «End Function».

Public Function My_fun()

End Function

Наша функция должна иметь один входной формальный параметр «Х». Поэтому в первой строке между скобками после имени функции пишем Х. Теперь надо записать саму процедуру вычисления функции. Возьмем ту же функцию, что и на листе Excel и введем ее в код функции между уже имеющимися строками, написав – Y=3*(Х-0.2)^3+15*Log(X). Здесь надо помнить, что разделителем десятичных знаков в коде программы является точка «.». Имена переменных лучше создавать латинскими буквами и не смешивать их с русскими, т.к. поиск ошибок в данном случае становится очень сложным из-за одинакового написания ряда символов. Чтобы сообщить системе, что надо возвращать из функции, дописываем еще одну строку – My_fun=Y. Можно было сразу же в первой строке вместо Y записать My_fun, мы сделали так для того, чтобы показать, что наша функция может быть очень сложной и только последний оператор передаст результат в основную программу.

Public Function My_fun(X)

Y = 3 * ((X - 0.2) ^ 3) + 15 * Log(X)

My_fun = Y

End Function

Проверим работоспособность нашей функции. Для этого перейдем снова на «Лист1» и в первую ячейку третьего столбце запишем заголовок «My_fun», во вторую ячейку введем нашу функции используя мастер построения функции (см. рис.4), сначала выберем категорию – «Созданные пользователем» и там видим единственную функцию, которую мы только что создали. Выбираем ее и в качестве параметра указываем значение в текущей строке столбца «Х». После ввода маркером заполнения (+) растянем формулу на весь столбец, как и делали это во время построения вычислений в предыдущем столбце. Данные двух столбцов должны совпадать.

В

Рис.15. Корень уравнений

торая функция, которая нам понадобиться в дальнейшем это вычисление производной для любой функции. Вычисление производной будем выполнять численным методом. Существует достаточно много формул для вычисления производной в заданной точке исследуемой функции. Рассмотрим самый простой из них (рис.15). От заданной точки Х отступим на достаточно малую величину Δ по Х вправо и влево и найдем в них значения функции. Для вычисления производной воспользуемся формулой (1)

, (1)

где в числителе разность значений функции между правой и левой точками, а в знаменателе сумма двух шагов, на которые мы отступаем от точки. Надо помнить, что отнимать надо всегда от правой левую точку. Второй вопрос, как опередить шаг? Если мы ведем вычисления с точностью до 5%, то шаг должен быть не более 2% от значения аргумента Х. Принимаем шаг равный 1% от значения параметра, что приводит к следующему алгоритму расчета:

(2)

есть Х=0 принимаем шаг равным 0,01, в других случаях шаг равняется 0,01 от значения Х.

Теперь создадим данную функцию, назвав ее «Difr». Для этого вставляем новую процедуру с этим именем и вводим следующие операторы:

Public Function Difr(Xt)

If Xt <> 0 Then

dH = 0.01 * Xt

Else

dH = 0.01

End If

Difr = (My_fun(Xt + dH) - My_fun(Xt - dH)) / (2 * dH)

End Function

Т

Рис.16. Графики модельной функции и ее производной

еперь проверим ее работу, добавив в нашу таблицу еще один столбец с производной. Дополним график новыми данными и получим следующий вид (рис.16).

Для добавления новых данных надо вызвать контекстное меню диаграммы и выбрать команду «Исходные данные». В открывшемся окне выбрать закладку «Ряд» (см. рис.7б) и, используя кнопку «Добавить», внести новые данные – «Имя:» – выберете заголовок столбца или можно написать «Производная», как показано на рис.16, «Значения Х:» – данные из столбца Х без заголовка и «Значения Y:» – данные из столбца Difr без заголовка.

Недостатком данной функции является необходимость каждый раз создавать новую подпрограмму для новой функции пользователя, переписывая строку, где записана наша модельная функция «My_Fun». Нашу функцию лучше передавать в подпрограмму как фактический параметр. Попробуем исправить эту проблему.

Сначала сделаем копию нашей подпрограммы «Difr». Теперь изменим заголовок функции на «Dif_Ur» и добавляем еще один формальный параметр «Fn», определив его как строковая переменная, для исключения возможных ошибок при вызове команды Run, которая требует ввода имени подпрограммы в формате строки. Потом введем два новых оператора для вычисления значений функций на левой (YL) и правой (YR) границах, используя команду приложения «Run». Здесь мы встречаемся в необходимостью ввода служебных слов. Для их выбора можно пользоваться командой Ctrl+J. Разберем порядок ввода таких слов. Встаем на новую строку и вводим первую букву служебного слова, затем вызываем список служебных слов (Ctrl+J) и продолжаем ввод символов, наблюдая за показанным списком, пока не будет выбрано нужное слово или просто прокрутим список с поиском этого слова. Когда слово найдено, просто вводим символ, который должен следовать за ним (это точка или скобка), после этого слово автоматически достраивается и предлагается список объектов для завершения команды. В нашем случае порядок действий будет следующим. Встаем в конец строки «End If» и нажимаем «Enter». Курсор перемещается на начало следующей строки. Вводим имя переменной «YL=» латинскую букву «А», потом нажимаем «Ctrl+J», появляется список служебных слов. Продолжаем ввод символов «ppl», в списке появляется слово «Application». Вводим «.», список меняется на перечень объектов «Application». Продолжаем ввод нужных символов «ru», как только появляется объект «Run» и завершаем ввод открывающей скобкой «(».

Теперь водим нужные параметры, сначала имя нашей функции «Fun» и потом через запятую значение параметра Х. Так же вводим вторую строку для вычисления YR и изменяем последнюю строку программы в которой исправляем имя функции и вместо двух вызовов нашей модельной функции ставим вычисленные значения функций. Наша новая подпрограмма готова.

Public Function Dif_Ur(Xt, Fn as String)

If Xt <> 0 Then

dH = 0.01 * Xt

Else

dH = 0.01

End If

YL = Application.Run(Fn, Xt - dH)

YR = Application.Run(Fn, Xt + dH)

Dif_Ur = (YR - YL) / (2 * dH)

End Function

Попробуйте решить практическую задачу. Мы имеем полином третьего порядка, который может иметь от одного до трех корней. Чтобы их локализовать, надо построить графики перовой и второй производных и найти на них точки пересечения оси Х.

Для это сначала создадим новую функцию «My_fun1» вида

Public Function My_fun1(X)

My_fun1 = 1 - 3 * X - 0.75 * X ^ 2 + 0.5 * X ^ 3

End Function

И создадим еще одну подпрограмму, которая будет находить вторую производную, которая будет использовать в качестве первого вычисления функцию обращения к подпрограмме «Dif_Ur». Данная подпрограмма имеет следующий код:

Public Function Dif_Ur2(Xt, Fn As String)

If Xt <> 0 Then

dH = 0.01 * Xt

Else

dH = 0.01

End If

YL = Dif_Ur(Xt - dH, Fn)

YR = Dif_Ur(Xt + dH, Fn)

Dif_Ur2 = (YR - YL) / (2 * dH)

End Function

Теперь на втором листе книги построим новую таблицу расчета этой функции и ее производных. В первой строке заполним заголовки столбцов. Параметр Х заполним прогрессией от -3 до 4, во второй столбец внесем функция «My_fun1» со ссылкой на соответствующую ячейку столбца «Х», в третьем столбце поместим функцию «Dif_Ur» с ссылками на параметр «Х» и заголовок функции, определив эту ссылку как абсолютную (используем клавишу «F4»). Для второй производной используем новую функцию «Dif_Ur2» с теми же параметрами, что и в предыдущей ячейке. Теперь три ячейки с функциями можем выделить и затем растянуть на всю таблицу Вид таблицы с формулами показан на рис.17, а полная таблица с данными на рис.18.

Рис.17. Заголовки столбцов таблицы и вид формул второй строки

Н

Рис.18. Таблица расчетных данных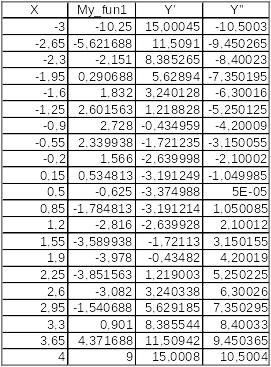

а основании данных таблицы строим график функции, который показан на рис.19. Как видим, в точках экстремумов производные превращается в 0. Это нам дает возможность определять как сами экстремумы, так и локализовать возможные области корней для исследуемых уравнений, что нам понадобится в следующих работах.

Рис.19. График полинома третьего порядка и его производных

Заключение

В результате выполнения работы были восстановлены приемы работы в среде Excel и VBA, которые будут использованы в следующих работах курса, а так же при выполнении расчетов во время курсовых и дипломных работ.

Самостоятельная работа

1. Реализуйте данную работу для других функций:

   1. 

Контрольные вопросы

1. Что такое функция пользователя?

2. Как создается и записывается код функций пользователя?

3. Опишите алгоритм вычисления производных.

Лабораторная работа № 2

Нахождение корней уравнения Введение

Корень уравнения, геометрический смысл, методы нахождения.

К

Рис.1 Корень уравнений

орнем уравнения считается число, при котором уравнения превращается в нуль. Существуют аналитические и численные методы нахождения корней уравнения. Первые из них позволяют получить алгебраическое выражение для вычисления корня, что бывает невозможно для ряда уравнений, которые называются трансцендентными. Вторые позволяют находить сами корни для любых уравнений с заданной точностью, но они часто требуют большого объема вычислений. Развитие вычислительной техники позволило в настоящее время широко использовать последние методы.

В графическом представлении корень показан на рис.1. К данной задаче можно привести и нахождение точки пересечения двух уравнений, используя их разность, как функцию, корень которой надо найти.

У

Рис.2 Корни квадратного уравнения

Рис.3 Существующий и несуществующий корни

равнения могут содержать несколько корней. В этом случае для их поиска надо выделить области, в каждой из которых находится только один корень. Чтобы понять этот процесс рассмотрим уравнение с двумя корнями (квадратное уравнение), график которого показан на рис.2. Как видно из графика корни, если они существуют у уравнения, лежат справа и лева от экстремума данной функции. Следовательно, надо найти экстремум и потом искать корни в двух интервалах – от -∞ до точки экстремума и от нее до ∞. Данный подход может быть распространен и на уравнения с большим количеством корней. Однако часть корней могут быть иррациональными числами (комплексными). Чтобы выполнить данную проверку надо сравнивать значения функции на концах отрезков, которые содержат корни – если эти числа имеют разные знаки, то корень существует.

Как это выглядит графически показано на примере кубического уравнения (может быть до 3-х корней) (рис.3). Как видно области первого и второго корня лежат выше нуля оси Х, таким образом, они просто отсутствуют среди рациональных чисел.

Возникает вопрос, как найти экстремум функции. Наиболее простой вариант этого решения – взять производную для уравнения по Х и найти корень полученной функции. Вычисление производных так же можно выполнить численным методом, рассмотренным в предыдущей работе.