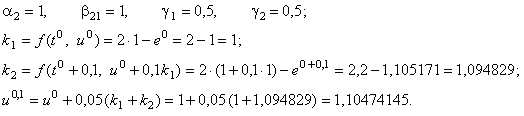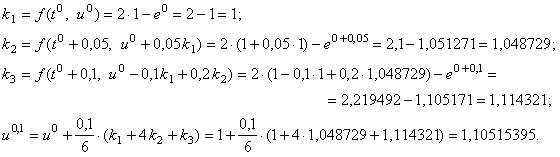Ме́тоды Ру́нге — Ку́тты

Ме́тоды Ру́нге — Ку́тты — важное семейство численных алгоритмов решения обыкновенных дифференциальных уравнений и их систем. Данные итеративные методы явного и неявного приближённого вычисления были разработаны около 1900 года немецкими математиками К. Рунге и М. В. Куттой.

Формально, методом Рунге — Кутты является модифицированный и исправленный метод Эйлера, они представляют собой схемы второго порядка точности. Существуют стандартные схемы третьего порядка, не получившие широкого распространения. Наиболее часто используется и реализована в различных математических пакетах (Maple, MathCAD, Maxima) стандартная схема четвёртого порядка. Иногда при выполнении расчётов с повышенной точностью применяются схемы пятого и шестого порядков

Рассмотрим задачу Коши

Задано обыкновенное диф. уравнение первого порядка и начальное условие:

Тогда приближенное значение в последующих точках вычисляется по итерационной формуле:

Вычисление нового значения проходит в четыре стадии:

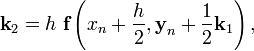
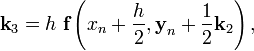
где   — величина шага сетки по  .

Прямые методы Рунге — Кутты

Семейство прямых методов Рунге — Кутты является обобщением метода Рунге — Кутты четвёртого порядка. Оно задаётся формулами

где   — величина шага сетки по   и вычисление нового значения проходит в   этапов:

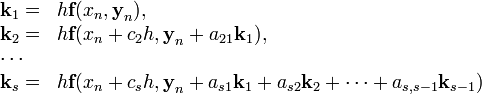
Конкретный метод определяется числом   и коэффициентами   и  . Эти коэффициенты часто упорядочивают в таблицу (называемую таблицей Бутчера)

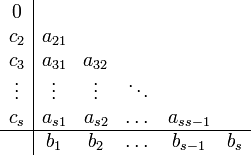
Для коэффициентов метода Рунге — Кутты должны быть выполнены услови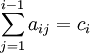я   для  .

Если требуется, чтобы метод имел порядок  , то следует также обеспечить условие

где   — приближение, полученное по методу Рунге — Кутты. После многократного дифференцирования это условие преобразуется в систему полиномиальных уравнений относительно коэффициентов метода.

 

Решение уравнений методом Рунге-Кутта.

Рассмотрим методику решения дифференциальных уравнений методом Рунге-Кутта на конкретном примере. Пусть задано дифференциальное уравнение с начальным условием:   (12.12) Требуется определить значение функции u в точке Значение шага по времени возьмём равным 0,1.       Видно, что решением уравнения (12.12) является функция  , значение которой в искомой точке составляет: Выполним решение уравнения (12.12), используя метод Рунге-Кутта с различными порядками точности, и сравним полученные результаты с истинным решением (следует отметить, что для данного уравнения явный и неявный методы Эйлера неприменимы, так как соответствующие им разностные схемы для уравнения (12.12) будут неустойчивы).       Рассмотрим методику решения уравнения (12.12) методом Рунге-Кутта 2-го порядка с использованием первого набора параметров: Видно, что ошибка появляется в третьей цифре после запятой.  Рассмотрим методику решения уравнения (12.12) методом Рунге-Кутта 2-го порядка с использованием второго набора параметров: Видно, что ошибка, как и в предыдущем случае, появляется в третьей цифре после запятой.        Рассмотрим методику решения уравнения (12.12) методом Рунге-Кутта 3-го порядка: Видно, что ошибка появляется в пятой цифре после запятой. Это наглядно доказывает, что метод Рунге-Кутта 3-го порядка более точен, чем метод Рунге-Кутта 2-го порядка.        Рассмотрим методику решения уравнения (12.12) методом Рунге-Кутта 4-го порядка: Видно, что ошибка появляется в седьмой цифре после запятой. Это наглядно доказывает, что метод Рунге-Кутта 4-го порядка более точен, чем методы Рунге-Кутта 2-го и 3-го порядка.

Система уравнений:

Метод позволяет решать системы обыкновенных дифференциальных уравнений (ОДУ) первого порядка следующего вида:

которые имеют решение:

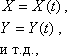
где t - независимая переменная (например, время); X, Y и т.д. - искомые функции (зависимые от t переменные). Функции f, g и т.д. - заданы. Также предполагаются заданными и начальные условия, т.е. значения искомых функций в начальный момент.

Одно диф. уравнение - частный случай системы с одним элементом. Поэтому, далее речь пойдет для определенности о системе уравнений.

Метод может быть полезен и для решения диф. уравнений высшего (второго и т.д.) порядка, т.к. они могут быть представлены системой диф. уравнений первого порядка.

Метод Рунге-Кутта заключается в рекурентном применении следующих формул:

Страница | 60

60