Заключение

В результате выполнения работы были разработаны программы для вычисления интеграла с использованием различных квадратурных формул. Выполнен анализ точности расчетов по каждой из формул. Создана функция пользователя, которая может быть использована в расчетах, когда надо будет вычислять интегралы.

Самостоятельная работа

5. Машин двигалась следующим образом – за 2 минуты она разогналась от 0 до 50 км/час, потом ехала с постоянной скоростью 25 минут, затем, выехав за город увеличила скорость до 100 км/час затратив на это 3 минуты. Через 15 минут машина достигла конечного пункта и остановилась, торможение длилось 5 минут. Найти пройденный машиной путь? Построить два решения – а: ускорения на всех участках с изменением скорости были постоянными; б: ускорения были изменяемыми от минимума к максимуму и обратно.

6. Разработать фрагмент программы «FDihot2» на случай отсутствия корня по время поиска необходимого интервала?

Контрольные вопросы

11. Что такое интеграл функции?

12. Как реализуется алгоритм интегрирования функции?

13. Какие модели используются для вычисления площади сечений при вычислении интегралов?

Понятие первообразной (метод Эйлера)

Первообрáзной^[1] или примити́вной функцией (иногда называют также антипроизводной) данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.

Первообразные важны тем, что позволяют вычислять интегралы. Если F — первообразная интегрируемой функции f, то:

Это соотношение называется формулой Ньютона — Лейбница.

Благодаря этой связи множество первообразных данной функции f называют неопределённым интегралом (общим интегралом) f и записывают в виде интеграла без указания пределов:

Если F — первообразная f, и функция f определена на каком-либо интервале, тогда каждая последующая первообразная G отличается от F на константу: всегда существует число C, такое что G(x) = F(x) + C для всех x. Число C называют постоянной интегрирования.

Каждая непрерывная функция f имеет первообразную F, одна из которых представляется в виде интеграла от f с переменным верхним пределом:

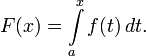
Существует три основных правила нахождения первообразных функций. Они очень похожи на соответствующие правила дифференцирования.

Правило 1

Если F есть первообразная дл некоторой функции f, а G есть первообразная для некоторой функции g, то F + G будет являться первообразной для f + g.

По определению первообразной F’ = f. G’ = g. А так как эти условия выполняются, то по правилу вычисления производной для суммы функций будем иметь: 

(F + G)’ = F’ + G’ = f + g.

Правило 2

Если F есть первообразная для некоторой функции f, а k – некоторая постоянная. Тогда k*F есть первообразная для функции k*f. Это правило следует из правила вычисления производной сложной функции.

Имеем: (k*F)’ = k*F’ = k*f.

Правило 3

Если F(x) есть некоторая первообразная для функции f(x), а k и b есть некоторые постоянные, причем k не равняется нулю, тогда (1/k)*F*(k*x+b) будет первообразной для функции f(k*x+b).

Данное правило следует из правила вычисления производной сложной функции:

((1/k)*F*(k*x+b))’ = (1/k)*F’(k*x+b)*k = f(k*x+b).

Приближённое нахождение первообразных(метод Эйлера)

Пусть на интервале   задана непрерывная функция   , для которой нужно найти первообразную   . Согласно определению первообразной, для этого нужно решить уравнение

(1.6)

найдя неизвестную функцию   . Относительно этой неизвестной функции уравнение является дифференциальным уравнением первого порядка. Его можно приближённо решать разными способами, которые вы будете изучать в курсе дифференциальных уравнений. Опишем здесь простейший из них, называемый методом Эйлера.

Из всего семейства первообразных   будем отыскивать ту первообразную, которая в некоторой фиксированной точке   принимает фиксированное значение   . Это условие выделяет из семейства первообразных одну функцию: все остальные первообразные   отличаются от этой фиксированной первообразной на постоянное слагаемое   и, следовательно, не удовлетворяют условию   .

Заметим, что из уравнения (1.6) следует, что

найденный дифференциал равен главной линейной части приращения функции:

откуда

Здесь мы учли начальное условие   . Тем самым, взяв некоторое приращение независимого переменного   , равное   , мы сможем приближённо найти значение первообразной   в "соседней" точке   :

Начав аналогичные вычисления с точки   вместо   , получаем

где   ; затем точно так же получаем

где   , и т. д. По найденным в известных точках   ,   ,   приближённым значениям первообразной   мы можем построить график функции   (разумеется, приближённо, поскольку значения   известны лишь приближённо). Выбирая   , мы построим этот график при   , то есть на   , а повторив процесс при   , построим часть графика на   .

Заметим, что шаг по оси   , то есть величину   , не обязательно выбирать одинаковым на всех этапах:   может зависеть от номера этапа   . Рекомендуется учитывать при этом выборе поведение функции   и уменьшать шаг   , если значения   увеличиваются, и увеличивать   , если значения   уменьшаются, чтобы величины приращений   были бы примерно одинаковы по абсолютной величине. Это даст возможность более точно построить график первообразной   .