В Рис.4. Алгоритм интегрирования функции ыполнение работы
Как и в предыдущих задачах реализуем решение несколькими способами – непосредственно на листе, с помощью макроса и через функцию пользователя с получением значения интеграла.
Для этого открываем новую книгу Excel, сразу же переходим в редактор VBA (Ctrl+F11) и создаем там модельную функцию, интеграл которой будем вычислять.
Public Function My_Fun(x)
My_Fun = 150 + 5.2 * x - 0.75 * x ^ 2
End Function
Теперь на первом листе книги готовим традиционную таблицу, которая должна иметь заголовок, потом подзаголовки с указанием формулы для решения и непосредственно столбца, которые нужны для расчета по этим формулам (рис.5).
Как обычно отмечаем светло-зеленым фоном ячейки, которые требуют ввода данных. В ячейку с размером шага записываем формулу dH=(Xк-Xн)/k, где все параметры в формуле ссылаются на ячейки отмеченные фоном. В ячейки 4 строки надо вписать формулу суммы всех площадей сечений для каждой формулы, так для столбца «Е» имеет вид =СУММ(E7:E26).Число охваченных формулой ячеек должно быть равным или больше чем значение k. После ввода первой формулы, остальные можно просто скопировать на остальные ячейки строки.
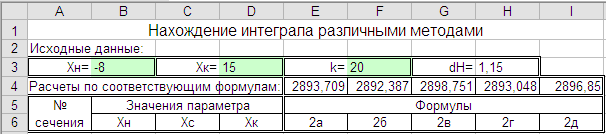
Рис.5. Заголовок основной таблицы
Теперь начнем заполнять остальные ячейки формулами. В первую очередь заполняем номера сечений, для этого в первую ячейку вводим 1 (рис.6), а последующие ячейки по данному столбцу заполняем формулой =A7+1.
Н
Рис.6. Формулы для
номера сечения
Рис.7. Формулы для
начала сечения
Т
Рис.8. Формулы для
средней и конечной точек сечения
=My_Fun(B7)*$H$3
=My_Fun(D7)*$H$3
=My_Fun(C7)*$H$3
=(My_Fun(B7)+My_Fun(D7))/2*$H$3
=(My_Fun(B7)+4*My_Fun(C7)+My_Fun(D7))/6*$H$3
Теперь остается скопировать все формулы от Хс до 2д и вставить их в следующую строку, а потом данную строку растянуть до необходимого числа сечений. Полученный результат, показанный на рис.9.
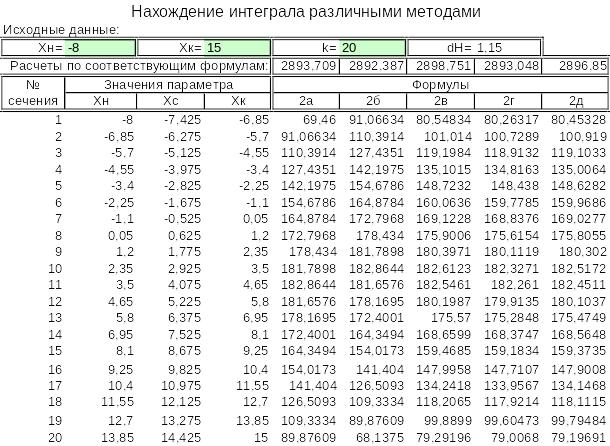
Рис.9. Результат вычисления интеграла модельной функции.
Как видим, результаты вычислений достаточно близки, говорит ли это об одинаковой точности всех этих формул. Попробуем провести анализ точности наших результатов в зависимости от используемой формулы. Для этого построим график нашей функции и попробуем найти интегралы на разных ее участках. Сначала формируем таблицу данных для нашего графика (рис.10), где берем интервал изменения параметра «Х» от -8 до 15, а «Y» определяем по нашей модельной функции. Теперь по этим данным строим график (рис.11).
Рис.10. Таблица для построения графика
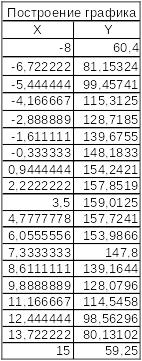
Рис.11. График модельной функции
И
Рис.12. Таблица для сравнение результатов
вычислений
Рис.13. Таблица разностей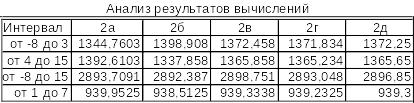
П
Рис.14. Гистограмма разностей в зависимости
от расположения интервалов
Теперь реализуем эту же задачу средствами VBA – создадим непосредственно функцию пользователя, которая сразу же возвращает значение интеграла. Сначала поставим задачу:
входными параметрами в программе должны быть границы интервала, точность решения, имя функции, которая используется в решении и номер формулы, которую будем использовать в расчетах;
реализуем алгоритм, показанный на рис.4;
для вычисления площади сечения создадим внутреннюю подпрограмму-функцию, которая на основании значений начальной точки сечения, шага, имени функции и номера формулы вычисляет площадь;
Переходим в редактор VBA и в модуле создаем функцию «Integral». Вводим формальные параметры в заголовок функции и заполняем собственно тело программы:
Public Function Integral(xn, xk, Fn As String, _
N_form, erf, Show As Boolean)
If erf = 0 Then erf = 0.01
k = 10: h = (xk - xn) / k
s = 0: xt = xn
For i = 1 To k
s = s + GetFun(xt, h, Fn, N_form)
xt = xt + h
Next i
Do
k = k * 2: h = (xk - xn) / k
s1 = 0: xt = xn
For i = 1 To k
s1 = s1 + GetFun(xt, h, Fn, N_form)
xt = xt + h
Next i
If Abs(s1 - s) < erf Then Exit Do
s = s1
Loop
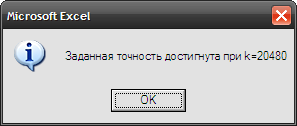
If Show Then
MsgBox "Заданная точность достигнута при k=" & k, _
vbInformation + vbOKOnly
End If
Integral = s1
End Function
Разберем программу более подробно. В первой строке проверяем задание точности вычисления для исключения ошибок при запуске программы. Потом задаем начальное значение k=10, вычисляем dH, обнуляем S и задаем Xt=Xн. В цикле от 1 до k суммируем площади сечений, обращаясь в внутренней функции GetFun и изменяем Xt. После организуем бесконечный цикл вычисления следующего значения интеграла в переменную S1, повторяя только, что описанные строки. Получив второе значение интеграла, проверяем условие достижения заданной точности в операторе If. При достижении заданного условия реализуем выход из цикла, иначе сохраняем значение S1 в S и повторяем вычисление интеграла еще раз. Для анализа скорости получения решения перед выходом из функции ставим вывод служебного окно (MsgBox) с сообщение числа k, при котором найдено решение. Если мы оставим это сообщение постоянно, то нам придется после каждого вычисления нажимать «Ok». Чтобы можно было управлять выводом этой информации внесем еще один формальный параметр «Show» как логическая переменная, которая может принимать два значения «ИСТИНА» и «ЛОЖЬ». Заключаем оператор с выводом окна в условный оператор «If». Теперь если переменная «Show» принимает значение «ИСТИНА», то вспомогательное окно выводится на экран.
Формируем программу вычисления площади «GetFun»:
Private Function GetFun(XX, dH, Fn, N)
Select Case N
Case 1
Y1 = Application.Run(Fn, XX)
Y = Y1 * dH
Case 2
Y1 = Application.Run(Fn, XX + dH)
Y = Y1 * dH
Case 3
Y1 = Application.Run(Fn, XX + 0.5 * dH)
Y = Y1 * dH
Case 4
Y1 = Application.Run(Fn, XX)
Y2 = Application.Run(Fn, XX + dH)
Y = (Y1 + Y2) / 2 * dH
Case 5
Y1 = Application.Run(Fn, XX)
Y2 = Application.Run(Fn, XX + dH)
Y3 = Application.Run(Fn, XX + dH / 2)
Y = (Y1 + Y3 * 4 + Y2) / 6 * dH
End Select
GetFun = Y
End Function
Т
Рис.15. Таблица расчета интегралов
Рис.16. Окно сообщения
