Тема7.Законбольшихчисел

Законбольшихчисел–это

—действиянадбольшимичислами

—правилавыполненияарифметическихдействийнадбольшимичислами

—законраспределениябольшогочисласлучайныхвеличин

—группатеоремосредниххарактеристикахслучайныхвеличинприбольшомчислеиспытаний

Последовательностьслучайныхвеличин

X_1,X_2,...,X_n,...^{называетсясходящейсяпо}

вероятностипрималом0

• X_nX

n

кслучайнойвеличинеХ,еслиприлюбомскольугодно

• n

  PXX

1

• 

  LimPXX

n ⁿ

1

• LimX_nX

n

ЛеммаМарковаоцениваетвероятностьтого,чтоположительнаяслучайнаявеличина

Хнепревзойдет

—еедисперсии

—еесреднегоквадратическогоотклонения

—предельнойошибки

—t²

• кратногоматематическогоожидания

ИзобобщеннойтеоремыЧебышеваследует,чтоеслидисперсиипопарно

независимыхслучайныхвеличинограниченысверхуконстантой

C0,то

—средняяарифметическаяслучайныхвеличинравнасреднейарифметическойих

математическихожиданий

—средняяарифметическаяслучайныхвеличинравнаматематическомуожиданиюоднойизних

—средняяарифметическаяслучайныхвеличинбольшесреднейарифметическойих

математическихожиданий

—средняяарифметическаяслучайныхвеличинсходитсяповероятностиксреднемуарифметическомуихматематическихожиданий

^{1n 1n} 

ИзобобщеннойтеоремыЧебышеваследует,что_P

^X_i^

^M(X_i^{)}

—равна1

—равна0

—больше,чем_1

C

n²

_ni1

_ni1 _

—равна_1

C

n²

НеравенствоЧебышеваоцениваетвероятностьтого,чтоотклонениеслучайнойвеличиныХотеематематическогоожидания

—положительно

• отрицательно

—поабсолютнойвеличиненепревзойдетопределенногоположительногочисла

—поабсолютнойвеличинепревзойдетопределенноеположительноечисло

ИзнеравенстваЧебышевасвероятностью,большей,чем_1^D(X)

_2

можноутверждать,

чтоабсолютнаявеличинаотклоненияслучайнойвеличиныХотеематематического

ожидания

—больше,чем0

—непревзойдет0

—равна0

—равна0

ОценочноенеравенствообобщеннойтеоремыЧебышеваоцениваетвероятностьтого,что

—абсолютнаявеличинаотклонениясреднегоарифметическогослучайныхвеличинот

среднегоарифметическогоихматематическихожиданийнепревзойдет0

—суммаслучайныхвеличиннепревзойдет0

—разностьслучайныхвеличиннепревзойдет0

—отклонениесуммыслучайныхвеличинотсуммыихматематическихожиданийне

превзойдет0

ПринеограниченномувеличениичисланезависимыхиспытанийсодинаковойвероятностьюпоявлениясобытияАвкаждомиспытании

—относительнаячастотасобытияАравнавероятностиэтогособытия

—относительнаячастотасобытияАсходитсяповероятностиквероятностиэтогособытия

—относительнаячастотасобытияАбольшевероятностиэтогособытия

—относительнаячастотасобытияАменьше,чем0

Законбольшихчиселявляетсятеоретическимобоснованием

—выборочногометода

—статистическойпроверкигипотез

—интегральнойтеоремыЛапласа

—формулкомбинаторики

Законбольшихчиселгласит,чтосредняяарифметическаязначенийбольшогочисласлучайныхвеличин

—являетсяслучайнойвеличиной

—стремитсякпостоянномучислу

—стремитсякслучайнойвеличине,имеющейпоказательноераспределение

—стремитсякслучайнойвеличине,имеющейбиномиальноераспределение

Центральнаяпредельнаятеоремаустанавливаетусловия,прикоторыхсуммаслучайныхвеличинимеетраспределение,близкое

—кпоказательномураспределению

—кравномерномураспределению

—кбиномиальномураспределению

—кнормальномураспределению

Иззаконабольшихчиселследует,чтонасреднемрезультатевоздействиябольшогочислаявленийвоздействиеодногоизэтихявлений

—несказывается

—сильносказывается

—малосказывается

—являетсяпреобладающим

ЛеммаМарковаутверждает,чтоположительнаяслучайнаявеличинанепревосходит

t^2кратногоматематическогоожиданиясвероятностью,большей

• 1

2

_—1

t

_—1

_t2

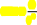—1¹

_t2

НеравенствоЧебышеваутверждает,чтовероятностьотклоненияслучайнойвеличиныХотеематематическогоожиданиянавеличинубольше,чем

_—1



• 1

2

—1

_—1D(X)

_2

P

ИзтеоремыБернуллиследует,что

^mp

^





^—¹

2

_—pq

_2

ⁿ 

—¹



^—1

pqn²

^{ВтеоремеПуассона,входящейвзаконбольшихчисел,p}

n

_p_i

_—i1

n

2

n

_p_i

_—i1

n

^m

^—M_{ }

^n

n

_p_imi

^—_i1

n

_m_i

i1

^{ВтеоремеПуассона,входящейвзаконбольшихчисел,pq}

n

_p_iqi

_—i1

n

2

2

n

q

^pi i

_—i1

n

^m

^—M_{ }

^n

n

_p_iqimi

^—_i1

n

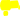_m_i

i1

m 

^{ИзтеоремыПуассонаследует,чтоP}



^—¹

2

• _pq



• _pq

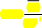n²

^{p}

n _

—1

pqn²

ОбобщеннаятеоремаЧебышеваутверждает,чтодляслучайныхвеличин,дисперсиикоторыхограниченысверхупостояннымчисломС,выполняетсянеравенство

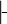^1ⁿ 1^{n }

P _X_{i }M(X_i)

n n

 ^i1

^i1 

• ^C

n

•  ^Cn²

—¹

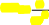n

—>_1

C

n²

ВтрактовкетеоремыЧебышева,называемой«Закономбольшихчисел»,

^1^{n }

утверждается,что

P _X_i

n

• M(X)



• ^C

n

^—¹

2

• _Cn

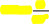n²

_ i1 _

^—>1

C

n²

ДлявыполненияцентральнойпредельнойтеоремыЛяпуноваобязательноусловие

—числослучайныхвеличинограничено

—случайныевеличиныимеютпоказательноераспределение

—случайныевеличиныраспределеныравномерно

—числослучайныхвеличиннеограниченноувеличиваются

ДлявыполненияцентральнойпредельнойтеоремыЛяпуноваобязательноусловие

—случайныевеличиныраспределеныравномерно

—случайныевеличиныимеютпоказательноераспределение

—случайныевеличинынезависимы

—числослучайныхвеличинконечно

ДлявыполненияцентральнойпредельнойтеоремыЛяпуноваобязательноусловие

—случайныевеличиныраспределеныравномерно

—случайныевеличиныраспределеныпопоказательномузакону

—случайныевеличиныимеютконечныематематическиеожиданияидисперсии

—случайныевеличиныимеютбиномиальноераспределение

ДлявыполненияцентральнойпредельнойтеоремыЛяпуноваобязательноусловие

—случайныевеличиныимеютбиномиальноераспределение

—случайныевеличиныраспределеныравномерно

—числослучайныхвеличинконечно

—ниоднаизслучайныхвеличинневыделяетсяпосвоемудействиюнасумму

ИзЛеммыМарковаследует,что

_—1

t

_—1

_t2

—1¹

t

PX

t^2M(X)

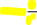—1¹

_t2

Вгруппутеоремзаконабольшихчиселневходит

—теоремаБернулли

—теоремаПуассона

—обобщеннаятеоремаЧебышева

—теоремаЛапласа

Вгруппутеоремзаконабольшихчиселневходит

—теоремаБернулли

—теоремаПуассона

—неравенствоЧебышева

—теоремаКоши

Вгруппутеоремзаконабольшихчиселневходит

—неравенствоЧебышева

—теоремаБернулли

—теоремаПуассона

—теоремаЛагранжа

ВнеравенствеЧебышева

_—D(X)

_2

_—1



_—1D(X)

_2

_—1D(X)

_2

PXM(X)

m 

ВпредельнойформетеоремаПуассонаутверждает,что

^imP

^{p}⁼

—0

• 1

2

—const

—1

n _{n }

ПредельнаяформаобобщеннойтеоремыЧебышеваутверждает,что

^1ⁿ 1^{n }

imP _X_{i }M(X_i)⁼

n n

n _

—0

• 1

2

^—

—1

i1

^i1 

m 

ВтеоремеПуассона

^imP

• ^{p}^{1величинаpесть}

n _{n }

—средняягеометрическая

—средняяинтегральная

—средняяарифметическаявзвешенная

—произвольная

ОбобщеннаятеоремаЧебышевавыполняетсядляслучайныхвеличин,длякоторых

—математическиеожиданияограниченысверху

—вероятностинаступлениямалы

—суммавероятностейбольшеединицы

—дисперсииограниченысверхунекоторымпостояннымчислом

m  ^m

ВтеоремеПуассона

^imP

• ^{p}^{1величина}

является

n _{n  n}

—вероятностьюнаступлениясобытияА

—вероятностьюненаступлениясобытияА

—относительнойчастотойсобытияА

—вероятностьюдостоверногособытия

МатематическоеожиданиеслучайнойвеличиныХравно3,2.Вероятностьтого,чтоХнепревзойдет4,0,больше,чем

—0,20

—0,16

—0,43

—0,31

ДисперсияслучайнойвеличиныХравна0,15.НаибольшееотклонениеслучайнойвеличиныХотеематематическогоожиданияМ(Х)поабсолютнойвеличинесвероятностьюбольшей,чем0,5,равно

—0,31

—0,55

—0,16

—0,49

ВероятностьнаступлениясобытияАравна0,6.Проведено500независимыхиспытаний.Вероятностьтого,чтоабсолютнаявеличинаотклоненияслучайнойвеличиныХ–числанаступленийсобытияотматематическогоожиданияМ(Х)непревзойдет20,больше,чем

—0,5

—0,6

—0,7

—0,8

ДисперсияслучайнойвеличиныХравна0,6.Вероятностьтого,чтоабсолютнаявеличинаотклоненияслучайнойвеличиныХотеематематическогоожиданиянепревзойдет1,2,больше,чем

—0,387

—0,222

—0,583

—0,838

ВероятностьнаступлениясобытияАвкаждомиспытанииравна0,4.Проводится200испытаний.Вероятностьтого,чточислонаступленийсобытияотклонитсяотегоматематическогоожиданияпоабсолютнойвеличиненеболее,чемна16,больше,чем

—0,667

—0,813

—0,765

—0,973

Дисперсиякаждойиз2000случайныхвеличиннепревышает9.Вероятностьтого,чтоотклонениесреднейарифметическойэтихвеличинотсреднейарифметическойихматематическихожиданийпоабсолютнойвеличиненепревышает0,1,больше,чем

—0,45

—0,55

—0,65

—0,75

Вероятностьтого,чтоотклонениеслучайнойвеличиныХотМ(Х)поабсолютнойвеличиненепревзойдет0,5,больше,чем0,4.ДисперсияD(X)равна

—0,1

—0,15

—0,25

—0,3

Вероятностьтого,чтослучайнаявеличиныХнепревзойдет6,больше,чем0,75.МатематическоеожиданиеМ(Х)равно

—0,5

—1

—1,5

—2

МатематическоеожиданиеслучайнойвеличиныХМ(Х)=3.Вероятностьтого,чтослучайнаявеличиныХнепревзойдетa,больше,чем0,6.Значениеaравно

—1,8

—5

—3,6

—7,5

СлучайнаявеличинаХ–числонаступленийсобытияАвnнезависимыхиспытанияхсвероятностьюнаступлениясобытияАвкаждомиспытанииp=0,3.Вероятностьтого,чтоабсолютнаявеличинаотклоненияХотМ(Х)непревзойдет5,больше,чем0,16.Числоnравно

—100

—200

—150

—50

Вероятностьтого,чтоабсолютнаявеличинаотклоненияотносительнойчастоты^m

n

наступлениясобытиявnнезависимыхиспытанияхотвероятностиэтогособытия

p=0,25непревзойдет0,05,больше,чем0,7.Числоnравно

—100

—150

—200

—250

Дисперсиякаждойизnслучайныхвеличиннепревышает6.Вероятностьтого,чтоотклонениесреднейарифметическойэтихвеличинотсреднейарифметическойихматематическихожиданийпоабсолютнойвеличиненепревзойдет0,1,больше,чем0,5.Числоnравно

—1000

—1200

—1400

—1600

СлучайнаявеличинаХ–числонаступленийсобытияАв200независимыхиспытанияхсодинаковойвероятностьюp=0,2событияАвкаждомиспытании.Вероятностьтого,чтоХнепревзойдет80,больше

—0,3

—0,4

—0,5

—0,6

Вероятностьтого,чтоположительнаяслучайнаявеличиныХнепревзойдетt^2

кратногоматематическогоожидания,больше,чем

• 1

2

^5.Числоtравно

9

—

• 5

2

• 7

2

Вероятностьтого,чтослучайнаявеличинаXнепревзойдет9,больше,чем .МатематическоеожиданиеM(X)равно

• 1

5

—5

• 5

9

_—81

5