Тема5.Законыраспределенияслучайныхвеличин

СлучайнаявеличинаX,являющаясяпромежуткомвременимеждупоявлениямидвухсобытийпростейшегопотока,имеет

—нормальноераспределение

—биноминальноераспределение

—показательноераспределение

—распределениеПуассона

СлучайнаявеличинаX,являющаясячисломпоявленийсобытиявпростейшемпотокезапромежутоквремениt,имеет

—равномерноераспределение

—распределениеПуассона

—показательноераспределение

—нормальноераспределение

Есливероятностьнаступленияmсобытийвпромежуткевремени(t₀,t₀₊t)независитотчислапоявленийсобытийдоначалаэтогопромежутка,тоэтосвойствопотокасобытийозначает

—отсутствиепоследействия

—ординарность

—стационарность

—равномерность

Свойствопотокасобытий,заключающеесявпрактическойневозможностипоявлениядвухиболеесобытийзамалыйпромежутоквремени,означает

—стационарность

—отсутствиепоследействия

—ординарность

—непрерывность

Есливероятностьпоявленияmсобытийзапромежутоквремениtзависиттолькоотчислаmивеличиныэтогопромежутка,топотоксобытийявляется

—ординарным

—непрерывным

—простейшим

—стационарным

Еслиn→∞,p→0,приэтомnp=a,тобиноминальноераспределениевпределедает

—показательноераспределение

—распределениеПуассона

—регулярноераспределение

—равномерноераспределение

Интенсивностьпростейшегопотокастечениемвремени

—стремитсяк_+∞

^{—стремитсяк}∞

—стремитсяк0

—неизменяется

Графикплотностинормальногораспределенияназывается

—кривойГаусса

—кривойБернулли

—кривойПауссона

—кривойЛапласа

Нормальноераспределениеслучайнойвеличинывозникаеттогда,когдаварьированиеслучайнойвеличиныобусловленовоздействием

—малогочислафакторов

—большогочислафакторов

—редкимифакторами

—конечнымзаранееопределеннымчисломфакторов

Дискретнаяслучайнаявеличина,выражающаячислопоявлениясобытияАвnнезависимыхиспытаниях,проводимыхвравныхусловияхисодинаковойвероятностьюпоявлениясобытиявкаждомиспытании,называетсяраспределеннойпо

—нормальномузакону

—позаконуПуассона

—биномиальномузакону

—попоказательномузакону

Еслислучайнаявеличинаимеетбиномиальноераспределение,n–числонезависимыхиспытаний,аp–вероятностьнаступлениясобытия,томатематическоеожиданиевычисляетсяпоформуле

• M(X)n

• M(X)p

• M(X)npq

• M(X)np

Еслислучайнаявеличинаимеетбиномиальноераспределение,n–числонезависимыхиспытаний,аp–вероятностьнаступлениясобытия,тодисперсияслучайной

величинывычисляетсяпоформуле

• D(X)npq

• D(X)np

• D(X)np

• D(X)p

ВраспределенииПуассонаредкихсобытийпараметраравен

• ap

• anp

• an²

• ap²

Свойствостационарностипотокасобытийозначает,чтовероятностьпоявленияkсобытийзапромежутоквремени

—независитотчислаk

—независитотвеличиныпромежуткавремени

—зависиттолькоотчислаkивеличиныпромежуткавремени

—независитниотчислаkниотвеличиныпромежуткавремени

Длярасчетавероятностейошибокприокруглениипоказанийизмерительныхприборовиспользуют

—равномерноераспределение

—биномиальноераспределение

—распределениеПуассона

—нормальноераспределение

Функциянадежностисвязанас

—нормальнымраспределением

—биномиальнымраспределением

—равномернымраспределением

—показательнымраспределением

Математическоеожиданиеравномернораспределеннойслучайнойвеличинывычисляетсяпоформуле

• M(X)^ab

2

• M(X)^ab

2

• M(X)^ba

2

• M(X)ab

Дисперсияравномернораспределеннойслучайнойвеличинывычисляетсяпоформуле

• D(X)ba

• D(X)ba

(ba)²

• D(X)

12

• D(X)^ba

12

Вероятностьпопаданияравномернораспределеннойслучайнойвеличинывинтервал

;

a,bвычисляетсяпоформуле

• P(X

• P(X

• P(X

• P(X

)^{}

ab

)^{}

ab

)^{}

ab

)^{}

ba

Плотностьраспределенияслучайнойвеличиныспоказательнымраспределениемимеетвид

⁰

_—f(x)_

приx0;

x

_e

приx0

^e^xприx0;

_—f(x)_

_0,

приx0

^{0приx0;}

_—f(x)_

_ex

• f(x)e^x

приx0

Функцияраспределенияслучайнойвеличиныспоказательнымраспределениемимеетвид

^{0приx0;}

—^F(x)_x

_e

приx0

^0при

x0;

_—F(x)_

_1e

x

при

x0

^0при

x0;

—^F(x)_{ x}

_1e

• F(x)e^x

при

x0

Упоказательногораспределенияматематическоеожиданиеисреднееквадратическоеотклонение

—всегдаразличны

—всегдаразличаютсянаединицу

—всегдаравны

—всегдаравны1

Еслиинтенсивностьотказовработыэлемента,то это

—надежностьработы

—скоростьотказовработы

—вероятностьотказа

—наработканаотказ

Графикомплотностираспределенияравномернораспределеннойслучайнойвеличиныявляется

—кусочно-непрерывнаяфункция

—парабола

—гипербола

—экспонента

Дляравномернораспределеннойслучайнойвеличиныпараметрсвычисляетсяпоформуле

—cab

—c ¹

ba

—c ¹

ab

—cba

РаспределениеПуассонаимеет

—0параметров

—двапараметра

—одинпараметр

—трипараметра

Показательноераспределениеимеет

—0параметров

—трипараметра

—двапараметра

—одинпараметр

Нормальноераспределениеимеет

—двапараметра

—0параметров

—одинпараметр

—трипараметра

Среднееквадратическоеотклонениебиномиальнораспределеннойслучайнойвеличинывычисляетсяпоформуле

—(X)np

^—(X)

^—(X)

np(1p)np

—(X)np(1p)

ВраспределенииПуассонаредкихсобытийпри

• p

• pconst0

• p0

• p1

n

Вточке

10. aкриваяГауссаимеет

—точкуперегиба

—точкуминимума

—точкуразрыва

—точкумаксимума

Точки

x_1a

иx₂

a

являютсядлякривойГаусса

—точкамиперегиба

—точкамимаксимума

—точкамиминимума

—точкамиразрыва

Функцияплотностинормальногораспределениясматематическиможиданиемaисредне-квадратическимотклонениемзадаетсяформулой



(xa)²

• f(x)

¹ _e 2²

2

• f(x)



• f(x)



(xa)²



¹ _e 2²

2

1

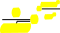(xa)²



_e 2

2



(xa)²

^—f(x) ¹ e ^2

 2

Вероятностьтого,чтонормальнораспределеннаяслучайнаявеличинаХ,имеющаяматематическоеожиданиеаисредне-квадратическоеотклонение,приметзначение

изинтервала

(c,d)

равна

  ¹

_da_

_ca_

• 

  P(c X d) ^_

^ 

^ _

^2^{  }

^{ }

P(cXd)¹

_ca_

_d a_







^{— } ^ ^ ^

^2^{ }

^{ }

P(cXd)¹

_da_

_c a_







^{— } ^^ ^

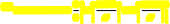^2^{ }

^{ }

P(cXd)^{da}^{ca}



^—    

^   

Вероятностьтого,чтоотклонениенормальнораспределеннойслучайнойвеличиныХ

отеематематическогоожиданиянепревзойдетпоабсолютнойвеличине0,равна

• PXa

^{}

• 

  

  PXa

_2_



_2_

• PXa

_{ }

^

^

• PXa

_{ }

^

РаспределениеПуассонахарактеризуетсятем,чтоегоматематическоеожиданиеидисперсия

—равнымеждусобой

—обратнопропорциональныдругдругу

—обаравны0

—отличаютсядруготдругана1

Потоксобытийназываетсяпростейшим,еслионобладаетследующимисвойствами

—стационарностью,отсутствиемпоследействия,независимостью

—стационарностью,отсутствиемпоследействия,ординарностью

—отсутствиемпоследействия,периодичностью,непрерывностью

—стационарностью,периодичностью,непрерывностью

Интенсивностьюпотоканазывается

—общеечислопоявлениясобытийвнаблюдаемыйотрезоквремени

—среднеевремямеждупоявлениемсобытий

—среднеечислопоявленийсобытийзаединицувремени

—общеевремямеждупоявлениемсобытий

Случайнаявеличина,являющаясячисломпоявленийсобытийвпростейшемпотокезафиксированныйпромежутоквремени,имеетраспределение

—нормальное

—биномиальное

—показательное

—Пуассона

Непрерывнаяслучайнаявеличина,являющаясяпромежуткомвременимеждупоявлениемдвухсобытийвпростейшемпотоке,имеет

—равномерноераспределение

—нормальноераспределение

—биномиальноераспределение

—показательноераспределение

Параметраминормальногораспределенияявляются

—математическоеожиданиеисредне-квадратическоеотклонение

—функцияраспределенияифункцияплотностираспределения

—функция(x)

и(x)

—дисперсияисредне-квадратическоеотклонение

Еслиплотностьраспределения

_cприxa,b

f(x)

непрерывнойслучайнойвеличиныимеетвид

 

f(x)_

_0приxa,b

,гдес=const,тоэтаслучайнаявеличинаимеет

—нормальноераспределение

—равномерноераспределение

—показательноераспределение

—биномиальноераспределение

Плотностьнормальногораспределенияопределяетсяформулой

(xa)²

• f(x)

• f(x)

¹_e2²





1 _e

2

(xa)²

2²

_x2

• f(x)



^{1 }2



e

2

• f(x)



(xa)²



¹ _e 2²

2

Случайнаявеличинаравномернораспределенанаотрезке[2,6].Еедисперсияравна

• 1

7

—3

• 4

3

—2

Случайнаявеличинаравномернораспределенанаотрезке[2,8].Еематематическоеожиданиеравно

—2

—3

—8

—5

Случайнаявеличинаимеетбиномиальноераспределениеспараметрамиn=40иp=0,3.Еематематическоеожиданиеравно

—3

—18

—12

—10

Случайнаявеличинаимеетбиномиальноераспределениеспараметрамиn=20иp=0,4.Еедисперсияравна

—9

—4,8

—13

—2,1

Соответствиемеждувозможнымизначениямидискретнойслучайнойвеличиныивероятностямиихпоявленияназывается

—закономраспределениядискретнойслучайнойвеличины

—закономбольшихчисел

—вероятностнымсоотношением

—пределомдискретнойслучайнойвеличины

Непрерывнуюслучайнуювеличинуможнозадатьспомощью

—рядараспределения

—функциираспределения

—полигонараспределения

—вероятностнойтаблицы

ФункцияраспределенияслучайнойвеличиныXзадаетсяформулой

• FxPX

• FxPX

• FxPX

• FxX

x

x

x

Графикфункциираспределениядискретнойслучайнойвеличиныпредставляетсобой

—непрерывнуюлинию

—кривуюГаусса

—изображениеотдельныхточекнаплоскости

—ступенчатуюразрывнуюлинию

Суммавеличинвсехскачковнаграфикефункциираспределениядискретнойслучайнойвеличиныравна

—1

—0

—

—произвольномучислу

Графическоеизображениефункцииплотностираспределенияназывается

—эмпирическойкривой

—кривойраспределения

—графикомслучайнойвеличины

—вероятностнойкривой

Дисперсиянепрерывнойслучайнойвеличины,заданнойнаинтервалеa;b,вычисляетсяпоформуле

b

—DX_x^2fxdxMX²

a

• b

  DX_x^2fxdx

a

b

—DX_x^2fxdxMX²

a

• b

  DX_xfxdxMX

a

ИнтегралПуассона

—

—2

• 

^ x²



_e^2dx



равен

— 2

Графикомфункциираспределенияравномернораспределеннойслучайнойвеличиныявляется

—непрерывнаяломанаялиния

—непрерывнаякривая

—разрывнаяступенчатаялиния

—криваяГаусса

Функцияплотностираспределенияслучайнойвеличиныспоказательнымраспределениемимеетвид

_0приx0;

_—fx_{ }

_e^xприx0

^{0приx0;}

—^{fx}_

_e^xприx0

^{0приx0;}

_—fx_{ }

_e^xприx0

_0приx0;

_—fx_{ }

_e^xприx0

Графикплотностивероятностиравномернораспределеннойнаотрезке[1;5]случайнойвеличиныXимеетвид:

fx

с

-1 0 ^{5 x}

Тогдазначениеcравно

• 1

4

• 1

3

• 1

6

—1

Графикплотностивероятностиравномернораспределеннойнаотрезке[3;4]случайнойвеличиныXимеетвид:

fx

с

-3 ^{0 4 x}

Тогдапостояннаяcравна

• 1

7

—1

• 3

4

• 4

3

Графикплотностивероятностиравномернораспределеннойнаотрезке[2;6]случайнойвеличиныXимеетвид:

fx

с

-2 ₀ 6 ^x

Тогдапостояннаяcравна

• 1

2

• 1

3

—1

• 1

8

ТочечнаяоценкаматематическогоожиданияраспределенияСBравна7.Тогдаегоинтервальнаяоценкаможетиметьвид

—(6,3;7)

—(7;7,5)

—(6,4;7,3)

—(6,2;6,8)

ТочечнаяоценкадисперсиираспределенияСBравна9.Тогдаееинтервальнаяоценкаможетиметьвид

—(8,3;9,2)

—(9;10,2)

—(8,1;9)

—(9;10)

ТочечнаяоценкаматематическогоожиданияраспределенияСBравна3.Тогдаегоинтервальнаяоценкаможетиметьвид

—(2,1;3)

—(2,4;3,3)

—(3;3,8)

—(3,7;4,2)

ТочечнаяоценкадисперсиираспределенияСBравна2.Тогдаееинтервальнаяоценкаможетиметьвид

—(1,3;2)

—(2;2,8)

—(2,4;3,1)

—(1,8;2,5)

СлучайнаявеличинаXраспределенапонормальномузакону.ВероятностьравнаФ(4).Параметрынормальногораспределенияравны

—a=1,

—a=2,

—a=2,

—a=2,

ПараметрынормальногораспределенияслучайнойвеличиныXравны:

a=5,	причем	.Значение	равно
—2
—2,5
—0,5
—1

Ошибкаизмерениянормальнораспределеннаяслучайнаявеличинасдисперсией,равной16.Систематическаяошибкаравна5.Вероятностьтого,чтоошибкаизмеренияокажетсявинтервале(3;7),равна

—Ф(0,5)

—¹⁽Ф(1)Ф(0,5))

2

—Ф(1)Ф(0,5)

—¹⁽Ф(0,5)Ф(1))

2

ДисперсиянормальнораспределеннойслучайнойвеличиныD(X)=0,25.Свероятностью,близкойк1,можноутверждать,что

—

—

—

—

Свероятностью,близкойк1,можноутверждать,чтонормальнораспределеннаяслучайнаявеличинаXудовлетворяетусловию: .ДисперсияD(X)равна

—0,25

—1,25

—2,25

—2,5

ПараметрынормальногораспределенияслучайнойвеличиныXравны:a=4, .Тогдавероятность равна

—Ф(4)

—Ф(2)

—Ф(3)

—Ф(1,5)

Вероятностьтого,чтонормальнораспределеннаяслучайнаявеличинаX,имеющаяматематическоеожиданиеa=3исреднееквадратическоеотклонение=2,приметзначениеизинтервала(1;6),равна

—¹⁽Ф(1,5)Ф(1))

2

—¹⁽Ф(1,5)Ф(1))

2

—¹⁽Ф(1)Ф(1,5))

2

—Ф(1)Ф(1,5)