Тема4.Случайныевеличины.Числовыехарактеристикислучайныхвеличин

^{Математическоеожиданиеслучайнойвеличины(сX+Y),гдеcconst,X},Y^

независимыеслучайныевеличины,равно

^—cM(X)M(Y)

^—cM(X)M(Y)

• M(X)M(Y)

• M(X)M(Y)

^{Дисперсияслучайнойвеличины(сX+Y),гдеcconst,X},Y

случайныевеличины,равна

^—cD(X)D(Y)

^—c2D(X)D(Y)

• D(X)D(Y)

^—cD(X)D(Y)

независимые

ДисперсияразностидвухнезависимыхслучайныхвеличинXиYравна

• D(X)D(Y)

—0

• D(X)D(Y)

• D(X)D(Y)

МатематическоеожиданиепроизведениядвухнезависимыхслучайныхвеличинXиY

равно

• M(X)M(Y)

• M(X)M(Y)

• M(X)/M(Y)

• M(X)M(Y)

ИндикаторомсобытияАназываетсяслучайнаявеличина,которая

—равнаконстантеа>1

—равнаконстантеа<1

—всегдаравна1

—равна1,есливрезультатеиспытаниясобытиеАпроисходитиравна0,еслисобытиеАнепроисходит

Закономраспределениядискретнойслучайнойвеличиныназываетсясоответствиемежду

—возможнымизначениямислучайнойвеличиныирядомнатуральныхчисел

—возможнымизначениямислучайнойвеличиныивероятностямиихпоявления

—математическиможиданиемслучайнойвеличиныиеесреднимквадратическимотклонением

—возможнымизначениямислучайнойвеличиныиеематематическиможиданием

Суммавсехвероятностейзначенийдискретнойслучайнойвеличиныравна

—0

—

—1

—1

Математическоеожиданиедискретнойслучайнойвеличинывычисляетсяпоформуле

n

• ^x_i

i1

n

• ^(x_ii1

p_i)x_i

n

• ^x

i1

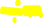n

2

i^p_i

• ^x_i^p_ii1

МатематическоеожиданиепостояннойвеличиныСравно

—С

—1

—0

—неопределено

^{Математическоеожиданиеслучайнойвеличины(сXY),гдеcconst,X},Y^

независимыеслучайныевеличины,равно

^—cM(X)M(Y)

• M(X)M(Y)

• M(X)M(Y)

^—cM(X)M(Y)

Дисперсиядискретнойслучайнойвеличиныопределяетсяпоформуле

n

• ^x_i^p_i

i1

n

2

^(^x_i^p_i⁾

i1

n

• ^x

i1

n

n

2 2 Ipi(xipi)

i1

₂ n

^—^x

i1

n

i^p_i

2

^^x_i^p_ii1

ⁿ 2

^—^x_i^p

i1

I(xipi)

i1

Существуютдвеформызаданиязаконараспределениядискретнойслучайнойвеличины:

—интегральнаяидифференциальная

—интегральнаяитабличная

—табличнаяиграфическая

—графическаяиинтегральная

ДисперсияпостояннойвеличиныСравна

—1

—C

—0

—неопределена

Среднееквадратическоеотклонение(x)случайнойвеличиныХравно

• D(X)

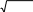• M(X)

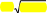• D(X)

—M(X)

Дисперсияотматематическогоожидания

—М(Х)

—0

—Х

—1

D(M(X))равна

Математическоеожиданиеотматематическогоожидания

—M(X)

M(M(X))равно

—0

—1

—D(X)

Математическоеожидание

—M(X)

—D(X)

—0

—1

M(XM(X))равно

Математическоеожиданиеквадратаотклонения

—D(X)

—(X)

—M(X)

—V

M(XM(X))^2равно

МатематическоеожиданиеM(X)случайнойвеличиныХесть

—переменнаявеличина

—+

—

—постояннаявеличина

Дисперсия

D(X)

непрерывнойслучайнойвеличины,заданнойнаинтервале

(a,b),

определяетсяформулой

b

^—D(X)_x^2f(x)dx(M(X))²

a

b

^—D(X)_(xM(X))f(x)dx

a

b

^—D(X)_(xM(X))^2dx

a

b

^—D(X)_(xM(X))dx

a

Существуютдвеформызаданиянепрерывнойслучайнойвеличины

—функцияраспределенияиплотностьраспределениявероятностей

—рядраспределенияиполигон

—функцияраспределенияирядраспределения

—функцияраспределенияиполигон

n

Выражение_x_ipi

i1

является

—дисперсиейдискретнойслучайнойвеличины

—вариациейдискретнойслучайнойвеличины

—математическиможиданиемдискретнойслучайнойвеличины

—среднимквадратическимотклонением

2

n _{2 }n _

Выражение_x_i

^p_i^_^x_i^p_i

является

i1

i1 

—дисперсиейдискретнойслучайнойвеличины

—вариациейдискретнойслучайнойвеличины

—математическиможиданиемдискретнойслучайнойвеличины

—среднимквадратическимотклонением

Величина,котораявзависимостиотрезультатовиспытанийпринимаеттоилииноечисленноезначение,называется

—постояннойвеличиной

—переменнойвеличиной

—случайнойвеличиной

—нормальнойвеличиной

Случайныевеличиныделятсяна

—переменныеипостоянные

—четныеинечетные

—рациональныеинерациональные

—дискретныеинепрерывные

Дискретнойназываетсятакаяслучайнаявеличина,котораяпринимает

—конечноеилибесконечноесчетноемножествозначений

—бесконечноемножествозначений

—толькооднозначение

—толькоотрицательныезначения

Графическаяформазаданиязаконараспределенияслучайнойвеличины–это

—парабола

—прямаялиния

—окружность

—полигон

Табличнаяформазаданиязаконараспределенияслучайнойвеличиныназывается

—суммойраспределения

—интеграломраспределения

—рядомраспределения

—полемраспределения

Непрерывнаяслучайнаявеличинаимеет

—конечноемножествозначений

—бесконечноесчетноемножествозначений

—конечноеилибесконечноесчетноемножествозначений

—бесконечноенесчетноемножествозначений

n n

2

Если_x_ipi

i1

10,а_x_ipi

i1

3,тодисперсияслучайнойвеличиныравна

—1

—3

—5

—7

Если(X)3,а(Y)2,то

—1

—5

—13

—16

Если(X)2,а(Y)1,то

—1

—3

—5

—9

D(X)D(Y)

D(X)D(Y)

Если

—1

—3

—5

—17

D(X)4;а

D(Y)1,то²⁽X)²⁽Y)

Указатьневерноезначениедисперсии

—1

—4

—9

—16

Указатьверноезначениедисперсии

—9

—4

—1

—1

Дискретнаяслучайнаявеличинапринимает

—толькомножествоцелыхзначений

—толькомножествоположительныхзначений

—всезначенияизинтервала;

—конечноеилибесконечноесчетноемножествозначений.

Непрерывнаяслучайнаявеличинапринимает

—множествоцелыхзначений

—множестворациональныхзначений

—конечноемножествозначений

—любоезначениеизконечногоилибесконечногоинтервала

ДлянепрерывнойслучайнойвеличиныXиконкретногозначенияaвероятность

PX

—0

—

—1

aравна

—

ЕслиXнепрерывнаяслучайнаявеличина,aиbконкретныезначения,тоотсюдаследует,что

• PaX

• PaX

• PaX

• PaX

bPaX

bPaX

bPaX

bPaX

b

b

b

bPaX

bPaX

b

Если

fxплотностьраспределения,то

b

_fxdx



присоответствующемзначенииb

можетпринятьзначение

—

—2

—1

—0,5

Если

fxплотностьраспределения,то

b

_fxdx



ниприкакихbнеможетпринять

значение

—1

—0,1

—0,4

—1

Математическоеожидание

MXнепрерывнойслучайнойвеличиныX,заданнойна

интервалеa,b,определяетсяформулой

• b

  MX_x^2fxdx

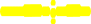a

• b

  MX_xfxdx

a

• a

  MX_x^2fxdx

b

• a

  MX_xfxdx

b

Если

—

—1

—0

—1

Если

fxплотностьраспределения,то

fxплотностьраспределения,то



_fxdx





_xfxdx



равен

определяет

• MX

• DX

—X

• FX

Если

fxплотностьраспределения,то



_xMx^2fxdx



определяет

• MX

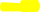• DX

—X

• FX

Если

fxплотностьраспределения,то

x

_fxdx



определяет

• MX

• DX

—X

• ^Fx

Если

fxплотностьраспределения,то

b

_fxdx



ниприкакихbнеможетпринять

значение

—1

—0,4

—0,6

—1,2

Случайнаявеличина,принимающаяконечноеилибесконечноесчетноемножествозначений,называется

—дискретной

—конечной

—бесконечной

—непрерывной

Случайнаявеличина,принимающаялюбыезначенияизконечногоилибесконечногоинтервала,называется

—дискретной

—конечной

—бесконечной

—непрерывной

ЕслиX2,аY1,то

—1

—3

—5

—7

DXYравна

Если

—39

DX9,

DY6,то

D3X2Yравна

—105

—57

—15

СлучайнаявеличинаXявляетсянепрерывной,еслиееинтегральнаяфункция

—непрерывнодифференцируема

—непрерывная

—имеетпредел

—убывающая

Fx

ЕслинепрерывнаяслучайнаявеличинаXпринимаетзначенияизинтервалаa;b,то

при

—1

—0

xb

функцияраспределения

Fxравна

—

—произвольномучислу

ЕслинепрерывнаяслучайнаявеличинаXпринимаетзначенияизинтервалаa;b,то

при

—1

xa

функцияраспределения

Fxравна

—

—0

—1

Дисперсия

DXCYравна

• DXC^2DY

• DXCDY

• DXCDY

• DXCY²

Математическоеожидание

—MXM^2X

• DX

—0

• 2MX

MXMXравно

Дисперсия

DC_1XC₂Yравна

—С₁DXC_2DY

—C^2DXC^2DY

1 2

—C^2DXC^2DY

1 2

—С₁DXC_2DY

ЕслиX2,

—7

—11

—25

—5

Y3,то

D2XYравна

Дисперсия

DC_1XC₂Yравна

—C₁DXC_2DY

—C^2DXC^2DY

1 2

—C₁DXC_2DY

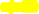—C^2DXC^2DY

1 2

СлучайнаявеличинаXзаданазакономраспределения:

X	4	2	3
P	0,3	0,5	0,2

Среднееквадратическоеотклонениеравно

—0,76

—2,4083

—0,8718

—2,8

ЗаконраспределенияслучайнойвеличиныХимеетвид:

X	2	1	3
P	0,4	0,1	0,5

Среднееквадратическоеотклонениеравно

—0,44

—1,1576

—1,9494

—0,6633

ЗаконыраспределенияслучайныхвеличинXиYимеютвид:

X	0,8	1
P	0,6	0,4

Y	0,7	0,8
P	0,7	0,3

ДисперсияD(XY)равна

—0,0117

—3,309

—0,0075

—3,699

Y	4	2
P	0,2	0,8

ДанызаконыраспределенияслучайныхвеличинXиY

X	2	3
P	0,4	0,6

МатематическоеожиданиеM(XY)равно

—0,2

—5

—0,6

—13,4

Если(Х)=3,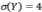 ,тоD(4X3Y)равна

—84

—12

—288

—24

Если(Х)=3,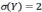 ,тоD(X2Y)равна

—25

—17

—7

—1

ДисперсияпроизведениядвухнезависимыхслучайныхвеличинXиYравна

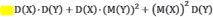—D(X)M(Y)+M(X)D(Y)

—

—D(X)D(Y)

—D(X)D(Y)+D(X)M(Y)+M(X)D(Y)

Y	4	2
P	0,3	0,7

ДанызаконыраспределенияслучайныхвеличинXиY

X	3	5
P	0,8	0,2

МатематическоеожиданиеD(X+Y)равно

—19,8

—4,6

—13,8

—1,48

Математическоеожиданиеслучайнойвеличины–числапоявленийсобытияАвnнезависимыхиспытанияхсвероятностьюpпоявленияводномиспытанииравно

—nq

—np

—n+p

—npq

Дисперсияслучайнойвеличины–числапоявленийсобытияАвnнезависимыхиспытанияхравна

—npq

—np

—

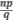
—np+q

Дисперсияслучайнойвеличиныимеетразмерность

—квадратаразмерностислучайнойвеличины

—случайнойвеличины

—кубаразмерностислучайнойвеличины

—корняквадратногоразмерностислучайнойвеличины

Y	4	5
P	0,6	0,4

ДанызаконыраспределенияслучайныхвеличинXиY

X	3	2
P	0,3	0,7

МатематическоеожиданиеM(XY)равно

—1,66

—12,33

—10,12

—8,76

Y	2	3
P	0,7	0,3

ДанызаконыраспределенияслучайныхвеличинXиY

X	3	5
P	0,4	0,6

МатематическоеожиданиеM(XY)равно

—7,28

—9,66

—5

—16,32

ЕслислучайнаявеличинаXестьчислонаступленийсобытияAспостояннойвероятностьювкаждомизnиспытаний,тозначенияслучайнойвеличиныначинаютсяс

—1

—0

—2

—∞

ЕслислучайнаявеличинаXестьчислоиспытанийсразличнойвероятностьюнаступлениясобытияAвкаждомиспытании,тозначенияслучайнойвеличиныначинаютсяс

—1

—∞

—0

—2

ЕслислучайнаявеличинаXестьчислонаступленийсобытияAсразличнойвероятностьювкаждомизnиспытаний,тозначенияслучайнойвеличиныначинаютсяс

—∞

—1

—0

—2

ЕслислучайнаявеличинаXестьчислоиспытанийспостояннойвероятностьюнаступлениясобытияAвкаждомиспытании,тозначенияслучайнойвеличиныначинаютсяс

—2

—0

—∞

—1