Тема3.Повторныенезависимыеиспытания

ПовторныминезависимымииспытаниямиотносительнособытияАназываютсяиспытания

—которыеповторяются

—которыеповторяютсяинезависятотдругихиспытаний

—которыепроводятсяводнихитехжеусловияхисодинаковойвероятностьюпоявлениясобытияАвкаждомиспытании

—вкоторыхсобытиеАповторяется

ВероятностьпоявлениясобытияАmразвnповторныхнезависимыхиспытанияхпри

n10

определяется

—формулойБернулли

—локальнойтеоремойЛапласаинтегральнойтеоремойЛапласа

—формулойПуассона

НаивероятнейшимчисломнаступленийсобытияАвnнезависимыхиспытанияхназывается

—наибольшеечислонаступленийсобытияА

—наибольшаявероятностьнаступлениясобытияА

—числонаступленийсобытияАпринаибольшемчислеиспытаний

—числонаступленийсобытияА,прикоторомвероятностьнаступлениясобытияАвnнезависимыхиспытанияхнаибольшая

1

_x2



(x) e

Функция ²

2

—четнаявозрастающаянечетнаяубывающая

обладаетследующимисвойствами

—четнаяположительная

—нечетнаяположительная

Функция

(x)

₂ x

0

2^e

t²



^2dt

обладаетследующимисвойствами

—нечетнаявозрастающая

—четнаявозрастающая

—нечетнаяубывающая

—четнаяубывающая

ЛокальнаятеоремаЛапласапозволяетвычислить

—наивероятнейшеечислонаступленийсобытиявnнезависимыхиспытаниях

—относительнуючастотунаступленийсобытиявnнезависимыхиспытаниях

—вероятностьпоявлениясобытияmразвnнезависимыхиспытаниях(n>10)

—вероятностьотклонениячислапоявленийсобытияmотчисланезависимыхиспытанийn

ИнтегральнаятеоремаЛапласапозволяетвычислить

—вероятностьпоявлениясобытияAmразвnиспытаниях(n>10)

—вероятностьпоявлениясобытияAвnиспытанияхнеменееа,нонеболееbраз(n

>10)

—наивероятнейшеечислопоявленийсобытияAвnнезависимыхиспытаниях(n>10)

—относительнуючастотунаступленийсобытияAвnнезависимыхиспытаниях

ИзследствияизинтегральнойтеоремыЛапласаследуетчто

—относительнаячастотапоступленийсобытияравнавероятностипоявленияэтогособытия

—относительнаячастотанаступленийсобытияотклонитсяотвероятностипоявленияэтогособытия

сувеличениемчислаnнезависимыхиспытанийвероятностьнаступлениясобытияувеличивается

—сувеличениемчислаиспытанийnотносительнаячастотавероятностипоявлениясобытияводномиспытании

^mприближаетсяк

n

Математическоеожиданиеслучайнойвеличины–числапоявленийсобытияАвn

независимыхиспытанияхсвероятностьюpнаступлениясобытияА–равно

• np²

• p

n

• 2

  p

n

• np

Дисперсияслучайнойвеличины–числапоявленийсобытияАвnнезависимыхиспытанияхсвероятностьюpнаступлениясобытияА–равна

• npq

• np

—p

• pq

ВероятностьпоявлениясобытияАmразвnнезависимыхиспытаниях

—зависиттолькоотmиn

—зависитотm,nиp

—зависиттолькоотm

—независитотmиn

ВероятностьпоявлениясобытияАmразвnповторныхнезависимыхиспытанияхпри

n10

определяетсяформулой

m

—_Cn

p^mq

nm

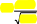_—(x)

npq

• _xmnp

npq

^—1(n)(m)

2

Вероятность

P(amb)^{появлениясобытияАвnповторныхнезависимых}

испытаниях(n>10)равна

^—1()()2

^—1(b)(a)

2

^—1()()2

^—1(b)(a)

2

ВлокальнойтеоремеЛапласа

^Pn,m^

(x)npq

аргументфункции(x)

равен

x ^mnpq

• _{x}np

npq

• _xmnp

npq

• xmnp

ВинтегральнойформулеЛапласа

()равен

P(amb)¹⁽()())_{,аргументфункции}

2

^—

anpq

_{—}np

npq

^—anp

_{—}anp

npq

ВинтегральнойформулеЛапласа

^{P(amb)1(()()),}аргументфункции

2

()

^—

равенbnpq

_{—}np

npq

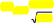• bnp

_{—}bnp

npq

^Pn,m

это

—вероятностьнаивероятнейшейчастоты

—вероятностьтого,чтоприnиспытанияхсобытиянаступитравноmраз

—условнаявероятностьсобытия

—вероятность,чтоприповторныхиспытанияхсобытиепроизойдетотmдоnраз

Приповторныхнезависимыхиспытанияхиспользуютсяформулы:а)Бернулли;б)

ЛокальнаяЛапласа;в)ИнтегральнаяЛапласа.Точнымиявляютсяб)

—a)

—в)

—б),в)

P(amb)

этовероятностьтого,чтоприnповторныхнезависимыхиспытаниях

событиепроизойдет

—ота(включительно)доbв(включительнораз)

• abраз

—большеаименьшеbраз

• ab

раз

Наивероятнейшеечисло

—толькооднозначение

m_0можетиметь

—либоодно,либодвазначения

—обязательнодвазначения

—тризначения

Дляслучайнойвеличины–числапоявленийсобытияАвnнезависимыхиспытанияхсвероятностьюpнаступлениясобытияАвыражениеnpявляется

—дисперсиейвариацией

—среднимквадратическимотклонением

—математическиможиданием

Дляслучайнойвеличины–числапоявленийсобытияАвnнезависимыхиспытанияхс

вероятностьюpнаступлениясобытияАвыражениематематическиможиданием

—дисперсией

—вариацией

—среднимквадратическимотклонением

np(1p)

является

Математическоеожиданиеслучайнойвеличины–числанаступленийсобытияАс

вероятностью

—45

—50

—30

—40

p0,4в

n100независимыхиспытанияхравно

Дисперсияслучайнойвеличины–числанаступленийсобытияАсвероятностью

p0,3в

—30

—21

—39

—23

n100независимыхиспытанияхравна

ВероятностьпоявлениясобытияA

mразвnповторныхнезависимыхиспытаниях

определяетсяформулойБернуллипри

—n10

—n100

—n100

—n10

Формуладляопределениянаивероятнейшегочислаm₀

имеетвид

• nppm₀

• npqm₀

• npqm₀

npp

npq

npp

• qm_0p

ВероятностьпоявлениясобытияАmразвnповторныхнезависимыхиспытанияхпри

n10

определяетсяформулой

^—1(n)(m)

2

m

^—C_n

p^mq

nm

_—(x)

npq

• _xmnp

npq

Выражение

_xmnp

npq

используетсяв

—локальнойтеоремеЛапласа

—интегральнойтеоремеЛапласа

—формулеБернулли

—формулеПуассона

Свероятностью,близкойк

(

^n),можноутверждать,чтопридостаточнобольшом

pq

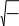числеиспытанийабсолютнаявеличинаотклонениячастости(относительнойчастоты,

доли)

• n

• p

• q

—

^mсобытияАотеговероятностиpнепревзойдетположительногочисла

n

P

ВследствииинтегральнойтеоремыЛапласа

^mp

^^{аргументфункции}





()

^—

равенnpq

ⁿ 

^—

^—

^—

npq



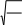
npq

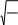pnq

Придостаточнобольшомчислеиспытанийабсолютнаявеличинаотклонениячастости

(относительнойчастоты,доли)

^mсобытияАотеговероятностиpнепревзойдет

n

положительногочисласвероятностью,близкойк



—

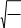 _n

 

 







—^

pq_

_p





_ nq_

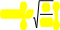 _n





—^ ^

_ pq_



—

 _ 

 

 

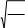
_ npq_

Еслипроводитсяnнезависимыхиспытаний,товкаждомизнихсобытиеАможетпроизойтисвероятностьюpилинепроизойтисвероятностью

—1p

• p1

—1p

• p1

ВероятностьнаступлениясобытияA

mразвnповторныхнезависимыхиспытаниях

при

n10определяется

—формулойПуассона

—формулойБернулли

—локальнойтеоремойЛапласа

—интегральнойтеоремойЛапласа

Формула

^mp^()^,где



ⁿ определяет

P





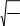_n _ pq

—локальнуютеоремуЛапласа

—интегральнуютеоремуЛапласа

—формулуПуассона

—следствиеинтегральнойтеоремыЛапласа

Выражение



ⁿ используетсяв

pq

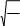
—следствииинтегральнойтеоремыЛапласа

—локальнойтеоремеЛапласа

—интегральнойтеоремеЛапласа

—формулеПуассона

Есличислонезависимыхиспытанийn=100,аматематическоеожиданиеслучайнойвеличиныравно40,товероятностьнаступлениясобытияАвкаждомизэтихиспытанийравна

—0,2

—0,4

—0,6

—0,8

ЕсливероятностьнаступлениясобытияАвкаждомизnнезависимыхиспытанийравна0,6,аматематическоеожиданиеравно120,тоnравно

—100

—200

—500

—1000

Указатьчислоповторныхнезависимыхиспытаний,прикоторомнерекомендуетсяиспользоватьформулуБернулли

—6

—8

—10

—12

Указатьчислоповторныхнезависимыхиспытаний,прикоторомрекомендуетсяиспользоватьлокальнуютеоремуЛапласа

—5

—8

—10

—13

ВероятностьнаступлениясобытияАвкаждомизnповторныхнезависимыхиспытанийравнаp=0,7,адисперсияравна21.Числоnравно

—50

—100

—10

—150

ЧислонаступленийсобытияА,прикоторомвероятностьнаступлениясобытияАвn

независимыхиспытанияхнаибольшая,называется

—наибольшейвероятностьюнаивероятнейшимчислом

—наибольшимчислом

—наивероятнейшимсобытием

Ввыражении

• np

• m

• npq

• npq

_xmnp

npq

среднимквадратичнымотклонениемявляетсявеличина

^{Величина} npq^{ввыражении}

—математическоеожидание

_xmnp

npq

представляетсобой

—среднееквадратичноеотклонение

—дисперсию

—вариацию

Есличислонезависимыхиспытаний

n100,аматематическоеожиданиеслучайной

величиныравно50,тосреднееквадратичноеотклонениеравно

—1

—3

—5

—7

Пределфункции

—1

—0

—1/2

—1

x

₂ x

0

2^e

t²



^2dt

при

x

равен

Дляфункции

x

₂ x

0

2^e

t²



^2dt

выполняетсясоотношение

—xx

—xx

—x^2x

—x

x

ДлязначенийaиbизинтегральнойтеоремыЛапласаимеютместосоотношения

• anp

• anp

• anp

• anp

npq,bnpnpq^,bnpnpq,bnpnpq,bnp

npqnpqnpqnpq

Дляфункции^{x}

—xx

—xx

—x^2x

2

x

₁ 

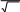^e2выполняется

2

—x

x

Функция^{x}

—1

—0

—1

—

2

x

₁ 

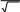^e2достигаетмаксимумаприx,равном

2

Приувеличениичислаиспытанийnотносительнаячастотавероятностипоявлениясобытия

—вбесконечномчислеиспытаний

—вnиспытанияхn10

—водномиспытании

—вдесятииспытаниях

^mприближаетсяк

n

Ввыражении

—дисперсией

_xmnp

npq

величинаnpявляется

—средне-квадратическимотклонением

—математическиможиданием

—вероятностьюнаступлениясобытияводномиспытании

Пределфункции^{x}

—

—1

—0

—1

2

x

₁ 

^e2при

2

x

равен

ИнтегральнаяфункцияЛапласа

—1

—

—0

—1

xпри

x

стремитсяк

Функция^{x}

—

—

—0

—1

2

x

₁ 

^e2при

2

x

стремитсяк

Врайонепосажены1000деревьев.Вероятностьтого,чтодеревонеприживется,равна0,08.Дляопределениявероятноститого,чтоизпосаженныхдеревьевнеприживутсяболее80деревьев,применяется

—локальнаятеоремаЛапласаинтегральнаятеоремаЛапласа

—формулаБейеса

—теоремаПуассона

Страхуется1500машин.Постатистикемашинаможетпопастьвавариюсвероятностью0,04.Дляопределениявероятноститого,чтосредизастрахованныхмашинколичествоаварийнепревзойдет90,следуетприменить

—статистическуювероятность

—локальнуютеоремуЛапласа

—формулуполнойвероятностиинтегральнуютеоремуЛапласа