Тема10.Корреляционно-регрессионныйанализ

Уравнениерегрессииотыскивается

—выборочнымметодом

—методоминтегрированиемпочастям

—методомнаименьшихквадратов

—методоммножителейЛагранжа

Корреляционнойзависимостьюназываетсястатистическаязависимость,прикоторойкаждомузначениюслучайнойвеличиныХставитсявсоответствие

—определенноезначениеслучайнойвеличиныY

—распределениеслучайнойвеличиныY

—корреляционноеотношение

—числоваяхарактеристикасоответствующегораспределенияслучайнойвеличиныY

Коэффициентавуравнениирегрессии

y_xaxb

показывает

—теснотусвязимеждуфакторнымирезультативнымпризнаками

—насколькоединицизменитсязначениерезультативногопризнакаприизменениифакторногопризнакана1единицу

—насколькопроцентовизменитсязначениерезультативногопризнака

—изменениефакторногопризнака

Еслиприравномерномвозрастаниизначенийфакторногопризнакасредниезначениярезультативногопризнакаравномерновозрастают,тоуравнениерегрессииотыскиваетсяввиде

—линейногоуравнения

—уравнениягиперболы

—уравненияпараболы

—уравнениятретьейстепени

Еслиприравномерномвозрастаниизначенийфакторногопризнакасредниезначениярезультативногопризнаканеравномерноубывают,тоуравнениерегрессииотыскиваетсяввиде

—линейногоуравнения

—уравнениягиперболы

—уравненияпараболы

—уравнениетретьейстепени

Универсальнымпоказателемтеснотысвязимеждуфакторнымирезультативнымпризнакамиявляется

—уравнениерегрессии

—корреляционноеотношение

—факторнаядисперсиярезультативногопризнака

—остаточнаядисперсиярезультативногопризнака



2

2

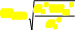Корреляционноеотношениеотыскиваетсяпоформуле

^—

_y_yx



2

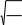y

_2

^—t ^y

n

2

^—

_yx



2

y



2

^— ^y

n

Cвязьмеждуфакторнымирезультативнымпризнакамиявляетсятесной,если

—1

—0

—1

^—

Линейныйкоэффициенткорреляцииопределяетсяформулой

^—

^2 ²

y

y

x



2

y

_—raxb

_x_y

^—r

_x_y

xyxy

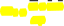_—rxyxy

_x_y

Вслучаелинейногоуравнениярегрессиисвязьмеждуфакторнымирезультативнымпризнакамиявляетсятесной,если

—r1

• r0

—r1

• r1

Общаядисперсиярезультативногопризнака–этомераколеблемостирезультативногопризнакаподвоздействием

—толькофакторногопризнака

—толькослучайныхфакторов

—всехфакторов,влияющихнаизменениерезультативногопризнака

—общегопризнака

Остаточнаядисперсиярезультативногопризнака–этомераколеблемостипризнакаподвоздействием

—толькофакторногопризнака

—толькослучайныхфакторов

—всехфакторов,влияющихнаизменениерезультативногопризнака

—общегопризнака

Cтатистическойназываетсязависимость,прикоторойкаждомузначениюслучайнойвеличиныХсоответствует

—определенноезначениеслучайнойвеличиныY

—произвольноезначениеслучайнойвеличиныY

—распределениеслучайнойвеличиныY

—постояннаявеличинавеличинаY

Корреляционнаязависимостьназываетсярегрессионной,есликаждомузначениюслучайнойвеличиныXсоответствует

—средняявеличинараспределенияслучайнойвеличиныY

—дисперсияслучайнойвеличиныY

—среднееквадратическоеотклонениеслучайнойвеличиныY

—определенноезначениеслучайнойвеличиныY

Парнаякорреляция–этозависимость,прикоторойрезультативныйпризнакYзависитот

—двухфакторныхпризнаков

—множествафакторныхпризнаков

—совокупностипар

(x_i;y_i)

—одногофакторногопризнакаХ

Задачейрегрессионногоанализаявляется

—определениеформысвязимеждуфакторнымирезультативнымпризнаками

—установлениетеснотысвязимеждуфакторнымирезультативнымпризнаками

—вычислениеошибкипоказателятеснотысвязи

—определениедоверительногоинтерваладляпоказателятеснотысвязи

Еслисвязьмеждуфакторнымпризнакомисреднимзначениемрезультативногопризнака–линейная,то

• r

• r

• r

• r

ЛинейныйкоэффициенткорреляцииопределяеттеснотусвязимеждупризнакамиХиY,еслисвязь

—линейная

—дробно-линейная

—гиперболическая

—квадратичная

Корреляционнаясвязьтемтеснее,чемменьшерассеяниемеждурезультативнымYифакторнымХпризнакамиподвлиянием

—учтенныхфакторов

—неучтенныхфакторов

—всехфакторов

—изучаемогофакторногопризнака

ЕсливлияниефактораХмалоосложняетсядействиемдругихфакторов,тозависимостьмеждуYиХявляется

—слабой

—случайной

—тесной

—остаточной

Определениезависимостипонаблюдаемымзначениям

—выравниваниемэмпирическихданных

—выпрямлениемэмпирическихданных

—осреднениемэмпирическихданных

—рассеяниемэмпирическихданных

10. и

y_{iназывает}ся

Согласнометодунаименьшихквадратовнаилучшейаппроксимирующейкривойбудетта,длякоторой

—среднееотклонениеординатэмпирическихточекотвыравненныхбудетминимальным

—квадратсреднегоотклоненияординатэмпирическихточекотвыравненныхбудетминимальным

—суммаотклоненийординатэмпирическихточекотвыравненныхбудетминимальной

—суммаквадратовотклоненийординатэмпирическихточекотвыравненныхбудетминимальной

Уравнение,связывающееусловнуюсреднюю

x_i,называется

—уравнениемрегрессии

—уравнениемтеснотысвязи

—гипотетическимуравнением

—корреляционнымуравнением

y ^{созначениемфакторногопризнака}

x

i

Корреляционномполемпеременных(х,у)называется



—совокупностьточек^xi

y



,y_i^

 i 

—совокупностьточек(х_i,у_i)накоординатнойплоскости

—изображениелиний,накоторойобозначеныточки(х_i,у_i)

—таблица,вкоторойданызначения(x_i+y_i)

Теснотасвязиэто

—отношениесуммызначений

—производнаяYпоX

y_iксуммезначенийx_i

—мерарассеяниярезультативногопризнакаYокололиниирегрессии

—мерарассеянияфакторногопризнакаХоколоуравнениярегрессии

Значениялинейногокоэффициентакорреляциипринадлежатпромежутку

^—0;)

^—0;1

^—0;2

^—1;1

Значениякорреляционногоотношенияпринадлежатпромежутку

^—0;)

^—0;1

^—0;2

^—1;1

Множественнаякорреляцияэтозависимость

—когдаодномузначениюxсоответствуетмножествозначенийy_i

—зависимостьрезультативногопризнакаотдвухиболеефакторныхпризнаков

—совокупностьпар(х_i,у_i)

—криволинейнаязависимостьмеждуXиY

Корреляционныйанализопределяет

—формусвязимеждуXиY

—производнуюY_x^

—теснотусвязимеждуXиY

• _xdx_ydy

Линия,построеннаяпонаблюдаемымзначениям

—теоретической

—выравнивающей

—эмпирической

—наблюдаемой

x_iи

y_iназывается

Системауравненийдляопределениякоэффициентовуравнениярегрессииназываетсясистемой

—параметрическихуравнений

—нелинейныхуравнений

—функциональныхуравнений

—нормальныхуравнений

Корреляционныйметодможетбытьприменен,есличислонаблюдений

—мало

—достаточновелико

—равно5

—равночислунаблюдаемыхзначенийx_i

ОпределениетеснотысвязимеждуфакторнымХирезультативнымYпризнаками–этозадача

—регрессионногоанализа

—выборочногометода

—корреляционногоанализа

—методанаименьшихквадратов

Уравнениерегрессиисвязываетзначенияфакторногопризнака

—определеннымзначениемрезультативногопризнака

—максимальнымзначениемрезультативногопризнака

—среднимзначениемрезультативногопризнака

—дисперсиейрезультативногопризнака

Линия,построеннаяпоуравнениюрегрессии,называется

—эмпирической

x_iс

—наблюдаемой

—выпрямляющей

—выравнивающей

Вуравнениирегрессии

_—xyxy y^2(y)²

• xyxy

_x_y

• xyxyx^2(x)²

y_xaxbкоэффициентаравен

₂ 2

_—x(x)

xyxy

x

Дисперсияфакторногопризнака

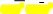—x^2(x)²

—x^2(x)²

—(x)^2x²

• xyxy

^2равна

ЗависимостьсреднейвыработкиодногорабочегозасменуY(шт)отквалификацииХ(разряды)приведенавтаблице:

Х	2	3	4	5
Y	12	19	23	30

Уравнениерегрессии

—2,8

—5,3

—5,8

—7,2

y_xaxb.Коэффициентaравен

ЗависимостьспросанаданныйтоварY(тыс.шт.)отсреднихдоходовнаселенияХ(тыс.руб.)приведенавтаблице:

Х	2	3	4	5
Y	5	11	15	23

Уравнениерегрессии

—1,2

—2,6

—4,4

—5,8

y_xaxb.Коэффициентaравен

ЗависимостьсреднегоприростаобъемавыпускаемойпродукцииY(тыс.шт.)откапиталовложенийХ(млн.руб.)приведенавтаблице:

Х	1	2	3	4
Y	6	7	9	10

Уравнениерегрессии

—1,9

—2,3

—3,2

—1,4

y_xaxb.Коэффициентaравен

Если

xy400,

x15,

y25,_x

3,_y

9,толинейныйкоэффициенткорреляции

^rвыб

равен

—0,926

—0,875

—0,975

—0,825

Если

—100

—13

—69

—11

x^2269,

x10,то_xравно

^{Если2100,}² 19^{,токорреляционноеотношение}^равно

—0,7

—0,8

—0,9

—1,0

Если

—10

—20

—40

—30

y

y^22500,

y_x

y40,то_yравно

Если

—4

—5

—6

—7,5

x^2169,

x12,то_xравно

^{Если2400,}² 39^{,токорреляционноеотношение}^равно

y _yx

—0,8

—0,85

—0,95

—1,0

Если

xy200,

x11,

y14,_x

6,_y

8,толинейныйкоэффициенткорреляции

^rвыб

равен

—0,925

—0,958

—0,875

—0,986

^{Если2100,0,95,то2}

равно

y _yx

—9,25

—9,5

—9,75

—10

Если

—81

—90

—84

y

—18

x9,_x

3,то

x^2равно

Если

—1,2

—1,3

—1,4

—1,8

y^21,69,

0,5,тоyравно