11. Числовые и функц.Ряды

Числовые ряды.

Будем рассм. обобщение суммы конечного числа слагаемых. Пусть имеем некоторую пос-ть U₀, U₁, …, U_n, … (1) U_n  R или U_n  C.

Составим формально выражение: U₀ +U₁ + …+ U_n + …= (2)

Выражение (2) будем наз. числовым рядом.

Запишем: U_0­ = S₀, U₀ + U₁ = S₁, …, U₀ + U₁ + … + U_n­ = S_n.

Рассм. пос-ть S₀, …, S_n (3). Эту пос-ть будем наз. пос-тью частичных сумм ряда (2). S_n – n-ая частичная сумма ряда (2). Поставим вопрос о -нии ?Если этот предел  и равен S, т.е. = S, (4) то S будем наз. суммой ряда (1) и писать = S.

Теорема: Пусть S = ,  = .Тогда = S +.

Критерий Коши: Для сх-ти ряда (2) необходимо и достаточно, чтобы для n>N pN, выполнялось нер-во: <  (5).

Вывод: Чтобы ряд (2) сх-ся необходимо выполнение условия = 0 – необходимый признак сходимости рядов.

Теорема: Для сх-ти ряда (2) при условии U_n  0, n, необходимо и достаточно, чтобы его пос-ть частичных сумм была ограничена сверху.

Т-ма(): Пусть имеем ряд (2) и ряд = V₀ + … + V_n + …, (6) причем выполнено условие 0  U_k  CV_k, k = 1, 2, …, C>0 (7). Тогда если ряд (6) сх-ся, то сх-ся и ряд (2).(под суммой к=1 и везде !)Если ряд (2) расх-ся, то расх-ся и ряд (6). (Это признак сравнения).

Вывод: Пусть ряды (2) и (6) имеют полож. члены, причем = L (8). Тогда имеет место следующее:

a) 0 < L < +  ряды (2) и (6) сх-ся и расх-ся одновременно.

б) L = 0  если ряд (6) сх-ся, то сх-ся и ряд (2)

в) L = +  если ряд (6) расх-ся, то расх-ся и ряд (2).

Признак Даламбера: Пусть имеем ряд .(2) Тогда:

1. 1) если  q < 1, n = 0, 1, 2, … (9), то ряд (2) сх-ся

2) если  1, n = 0, 1, 2, … (10), то ряд (2) расх-ся

2. (в предельной форме). Пусть для (2) имеем = q.

Если 0  q < 1, то ряд (2) сх-ся.Если q > 1, то ряд (2) расх-ся

Признак Коши: Пусть имеем (2), где U_n  0, n = 1, 2, …, тогда

1. 1) если  q < 1, n = 1, 2, …, то ряд (2) сх-ся.

2) если  1, n = 1, 2, …, то ряд (2) расх-ся.

2. (в предельной форме): пусть  lim = q, тогда

1) если q < 1, то ряд (2) сх-ся. 2) если q > 1, то ряд (2) расх-ся.

Замечание: в признаке Даламбера усл. (9) нельзя заменить на усл. < 1, n = 1, 2, …Например, гармон. ряд - расх-ся, но = < 1.

Замечание: Если в предельных признаках Даламбера и Коши q = 1, то о сх-си ряда ничего нельзя сказать. В этом случае следует применять другие достаточные признаки сходимости: признак Гаусса, признак Раабе и др.

Теорема(интегральный признак сх-ти рядов): Пусть имеем : [1; +)R, причем 1) (x)  0 x[1; +) 2)  - не возратстает на [1; +).Тогда ряд (13) будет сх-ся или расх-ся одновр. с интегралом (14).

Теорема: Пусть имеем сх-ся ряд (2) с полож. членами и имеющий сумму S. Тогда при любой перестановке его членов получим новый ряд, который также будет сх-ся и иметь сумму S.

Абсолютно и условно сходящиеся ряды.

Будем рассм. ряды, которые содержат бесконечное число полож. и отр. членов. Такие ряды наз. знакопеременными. Среди указанных рядов выделяют знакочередующиеся ряды, т.е. ряды вида: , U_n > 0, n = 1, 2, …Пусть имеем = U₀ + U₁ + … + U_n + … (1)Запишем ряд сост. из модулей членов, т.е. = U₁ + U₂ + … + U_n + … (2)

Можем считать U_n  R или U_n  C

Теорема: Если ряд (2) сх-ся, то сх-ся и ряд (1).Док-во: Чтобы убедиться в этом, применим критерий Коши: = U_n+1 + U_n+2 + … + U_n+p  U_n+1 + … + U_n+p = < , n>N, pN, -  полож. число  справедливость теоремы.Опр.: Если сх-ся ряд (2), то ряд (1) наз. абсолютно сх-ся.Опр.: Если ряд (1) сх-ся, а ряд (2) расх-ся, то ряд (1) наз. условно сх-ся. Теорема Коши: если ряд (1) сх-ся абсолютно, то при любой перестановке его членов получим новый ряд, который также абс. сх-ся и имеет ту же сумму.

Теорема Римана: Если ряд (1) сх-ся условно, то, каково бы ни было число а, можно переставить члены этого ряда так, чтобы сумма получившегося ряда будет равна числу а.

Преобразование Абеля.

Рассм. сумму = a₁b₁ + a₂b₂ + … + a_nb_n.

Положим B₁ = b₁­, B₂ = b₁ + b₂, …, B_n = b₁ + b₂ + … + b_n.

Тогда b₁ = B₁, b₂ = B₂ – B₁, …, b_n = B_n – B_n-1

и = a₁B₁ + a₂(B₂ – B₁) + a₃(B₃ – B₂) + … + a_n(B_{n –} B_n-1) =

= B₁(a₁ – a₂) + B₂(a₂ – a₃) + … + B_n-1(a_n-1 - a_n) + a_nB_n.

Отсюда = a_nB_n - (3)

Формула (3) наз. преобразованием Абеля.

Пусть заданы ряд (4) и ряд (5) B_n = - n-ая частичная сумма ряда (5)Признак Абеля: Если ряд (5) сх-ся, а пос-ть {a_n} монотонна и ограничена, то ряд (4) сх-ся.

Признак Дирихле: Если пос-ть {B_n} частичных сумм ряда (5) ограничена, а пос-ть {a_n} монотонно стремится к нулю, то ряд (4) сх-ся.

Функциональные ряды.

Пусть имеем _k: ER, ERⁿ, kN.Рассм. выражение ₁(x) + ₂(x) + … + _n(x) + … = (1). – функциональный ряд, который задан на мн-ве Е.Рассм. также S₁(x) = ₁(x), S₂(x) = ₁(x) + ₂(x), …, S_k(x) = ₁(x) + … + _k(x) И рассм. пос-ть S₁(x), S₂(x),…, S_k(x),… (2)

(2) – функциональная пос-ть частичных сумм.

Если для xE пос-ть (2) сх-ся и , (3) то будем говорить, что на Е ряд (1) имеет сумму S(x) и писать: = S(x), xE.Если же для некоторого xE предел (3) не существует, то будем говорить, что функциональный ряд (1) в этой точке расх-ся.

Опр.: Будем говорить, что ряд (1) сх-ся на мн-ве Е равномерно к ф-ии S(x), если

для  N=N()N, что для n>N и для xE вып-ся

S_n(x) – S(x) < , где S_n(x) – частичная сумма ряда (1).

Обозначение S_n(x)=> S(x), xE, n  

Критерий Коши: Ряд (1) сх-ся равномерно на мн-ве Е  для , что для n>N xE выполняется условие: < , pN (5)

Признак Вейерштрассе:Пусть имеем ряд (1) и числ. ряд a_n  0 Если_n(x) < a_n, nN, xE и - сх-ся. Тогда ряд (1) сх-ся на Е равномерно. Рассм. функциональный ряд (7)

Признак Абеля: Если ряд 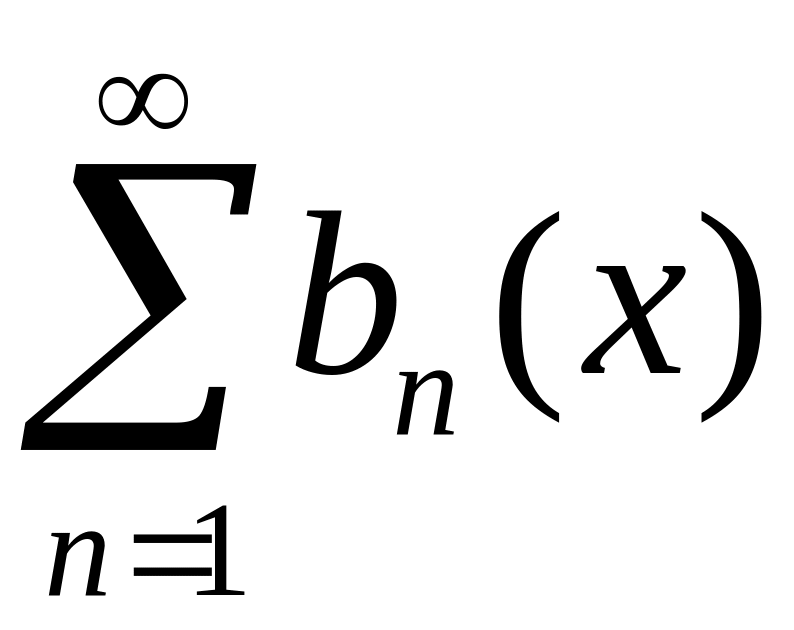(8) сх-ся на Е равномерно, а пос-ть {a_n(x)} монотонная и ограниченная на Е, тогда ряд (7) сх-ся равномерно на Е.Признак Дирихле: Когда частичные суммы B_n(x) ряда (8) ограничены на Е, а пос-ть {a_n(x)} монотонно и и равномерно стремится к нулю на Е, то ряд (7) сх-ся на Е равномерно.

Свойства равномерно сх-ся рядов и пос-тей.

1. Почленный переход к пределу, перестановка пределов.

Рассм. Ряд , xE (9), x₀ – предельная точка мн-ва Е.

Теорема: Пусть в (9) на Е сх-ся равномерно к сумме S(x) и сущ

1. = a_n (10)n=1,2,... То S(x) имеет предел в т-е x₀ причем 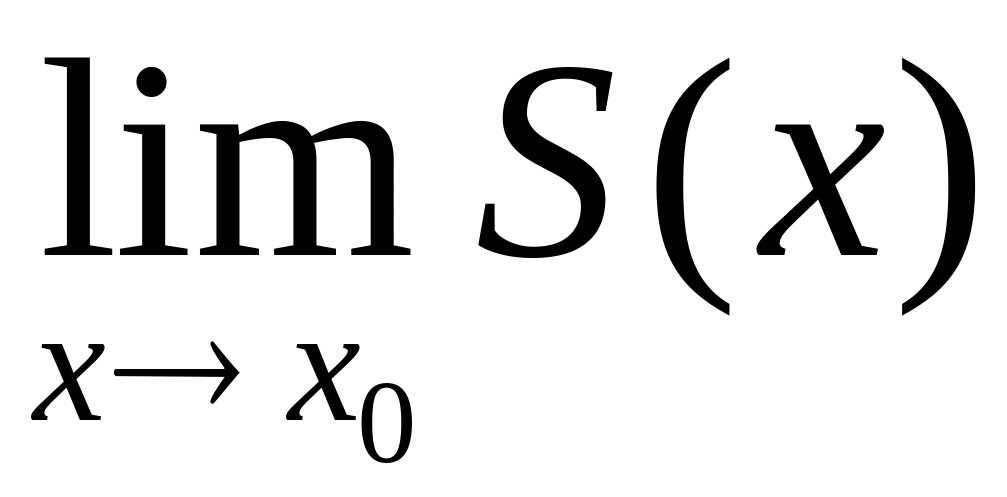= (12)

Замечание1: Из теоремы , что будет справедлива запись:

= (13)

Условие (12) принимает вид (13) и получается, что символы ∑ и lim перестановочны.

Замечание 2: Очевидно, что соот-ая теорема имеет место для пос-тей, которые равномерно сх-ся на Е. Тогда можно записать = (14).Рав-во (14) имеет место в случае, когда пос-ть {S_n(x)} равномерно сх-ся на Е.

2. Непрерывность суммы ряда.

Теорема: Если ф-ии _n(x), n = 1, 2, … непрерывны на Е и ряд (9) на Е равномерно сх-ся, то сумма S(x) ряда (9) непрерывна на Е.

Замечание: Теорема дает достаточные условие непрерывности суммы ряда.

3. Почленное интегрирование рядов.

Теорема: Пусть _n: [a, b]R, n = 1, 2, … _n – непрерывна на промежутке Е и ряд (9) сх-ся на Е равномерно к S(x). То этот ряд можно почленно интегрировать на любом [a, b] из Е , причем = , (15)

причем ряд, который записан в правой части (15) равномерно сх-ся на [a, b].

Замечание: Теорема – достаточные условия почленного интегрирования.

4. Почленное дифференцирование рядов.

Теорема: Пусть _n: [a, b]R непрерывно диф-мы на [a,b], на [a,b] и ряд (16) равномерно сх-ся на [a, b].Тогда если ряд (9) сх-ся на [a,b], то его сумма непрер-диф на [a,b], причем

= , если S(x) = (17)

п.3 Степенные ряды.

Опр.: Функц. Ряд вида (1) наз. степенным рядом, здесь a_n, z, z₀  C.Вместо (1) можно рассм. ряд (2), a_n, z  C, потому что ряд (1) можно привести к (2) заменой z = z – z₀. Т.о. вопрос о сх-си ряда (1) можно решить, рассм-ая ряд (2).

Первая теорема Абеля: Если ряд (2) сх-ся в точке z = z₀  0, то этот ряд будет абс-но сх-ся для z, z < z₀.

Следствие: Если ряд (2) расх-ся в т. z = z₁  0, то этот ряд расх-ся для всех z таких, что z > z₁.

Опр.: Если ряд (2) сх-ся для z, z < R и расх-ся для z, z > R ,то R наз радиусом сх-ти.Опр.: Мн-во K = {z  Cz  R}, где R – радиус сх-ти (2) наз. кругом сх-ти.

Если ряд (2) сх-ся при z = 0 и расх-ся при z  0, то R = 0,

Если ряд (2) сх-ся для z, то R = +.

Теорема: Каждый степенной ряд (2) имеет радиус сх-ти. При любом z ,z < R – ряд сх-ся абсолютно.Ряд (2) сх-ся равномерно на мн-ве z  r , 0 < r < R.

Следствие: Если R>0 – радиус сх-ти ряда (2), то его сумма явл-ся непрерывной ф-ей для z, z < R.

Вторая теорема Абеля: Пусть R > 0 – радиус сх-ти ряда (2) и ряд (2) сх-ся в т. z = R, тогда ряд (2) равномерно сх-ся на отрезке [0, R].

Теорема: Пусть R – радиус сх-ти ряда (2) и  = .тогда R = , (3)при ; R=0 при ; при =0.

(3)- формула Коши-Адамара.

Замечание: Если  , то R = .

Теорема: Рассм. ряды , , . Ряды эти имеют один и тот же радиус сх-ти.