5. Предел функции одной, нескольких переменных, отображений из в .

Пусть имеем , , a- предельная точка мн-ва X (т.е. т., окрестность кот. содержит точки из X, ≠a).

О1(по Коши). Число наз. пределом функции в точке , при , если , что для , что : .

О2(по Коши). Число наз. пределом ф-ции при , если для , то . О3(по Коши). Число наз-ся пределом ф-ии при , если , что если , то . О4(по Гейне). Число наз-ся пределом ф-ции , при , если для : , , , при : . Если некоторое число явл-ся lim по Коши, то оно явл-ся и lim по Гейне.

Т.1 О1 и О4 эквиволентны.

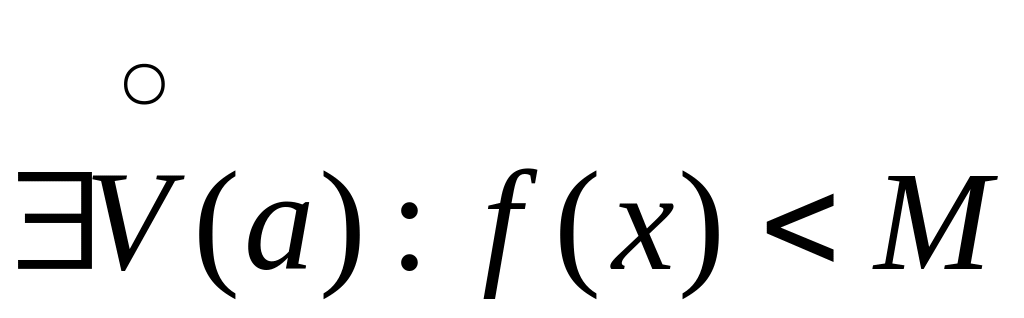О5. Функция наз. ограниченной на X, если , для . Функция наз. финально ограниченной при , если для 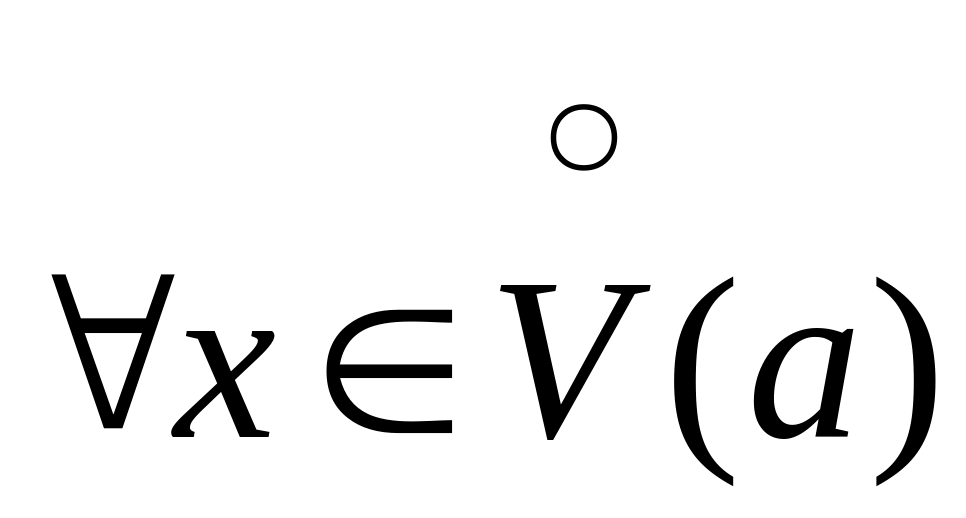. Т.2 1)Если при имеет предел, то она финально ограничена при . 2) Если в т. a имеет предел, то он единственный.

Св-ва предела ф-ции: Т3. Пусть , , тогда: 1) , , 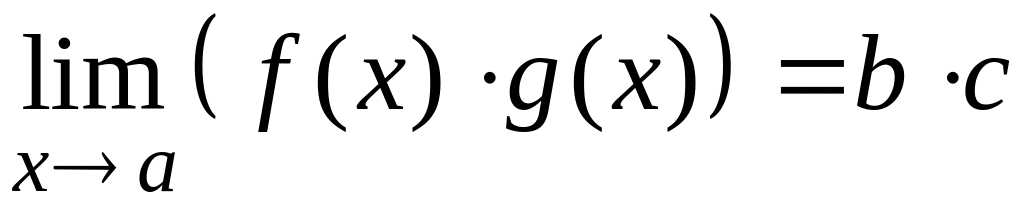. Т.4. Если , и . Тогда . Т5. Если , , , то ,что для . След: 1) ; 2) 3) ; 4. , .

Т6.(крит. Коши). Для существования , необх. и дост., чтобы , что выполняется нер-во .

О6. Пусть , если , то этот предел наз-ся правосторонним пределом функции в точке а.

О7. Пусть 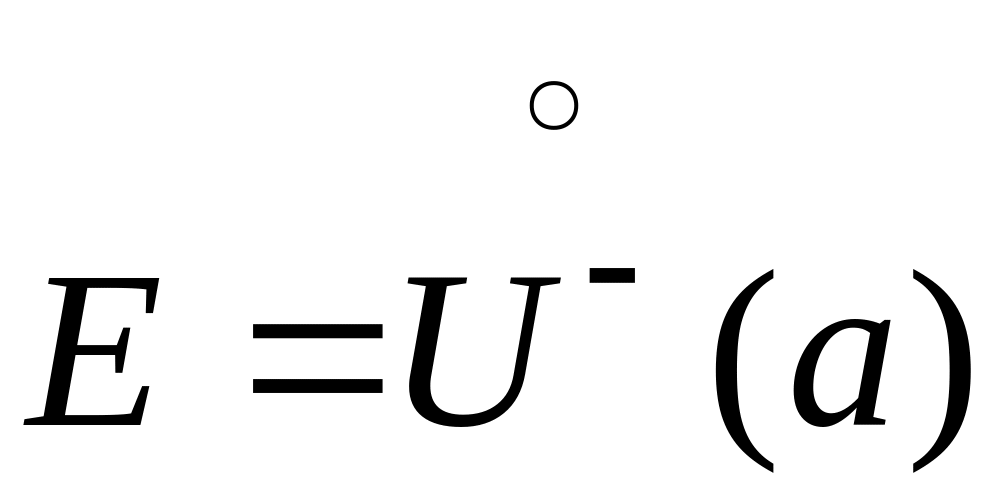, если , то этот предел наз-ся правосторонним пределом функции в точке а.

Пр , если ; если ; , если . ; .

Т7. Чтобы функция имела в точке a предел, необх. и дост. чтобы она имела в этой точке оба равных между собой односторонних предела.

Многомерный случай. Рассмотрим отображение , , который каждой т. мн-ва X из ставит в соответствие т. задание такого отображение равносильно заданию m ф-ций . Эти ф-ции наз. координатными ф-циями отображения . 1. –ф-ция одной переменной. 2. , , ф-ция n переменных. 3. -m вектор ф-ция. 4. – отображение. О8: Точка наз. пределом отображения , при (в точке а), если для , , что для , таких, что будет . Пишут . 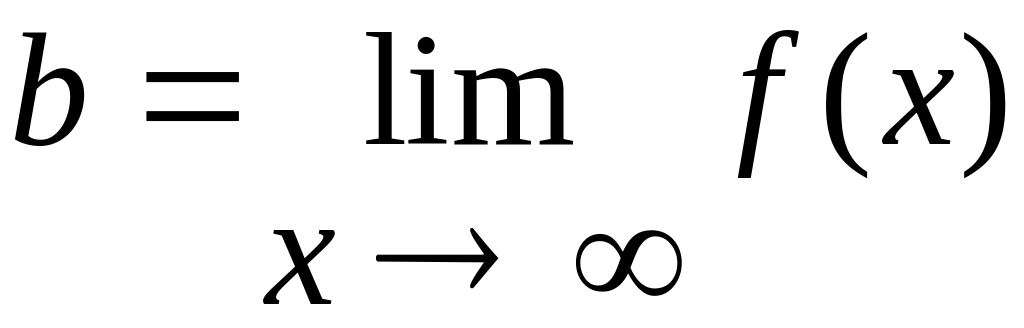Если , то ( ), причем ; ). Обозначим - окр-сть т. a в мн-ве X. 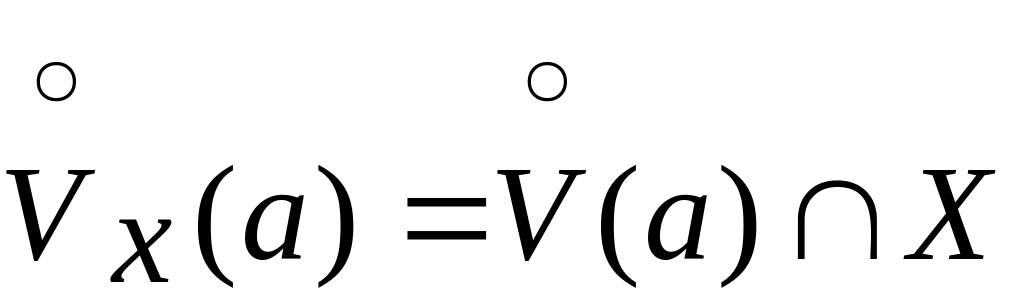- проколот. окр-ть т. a. О9: Точка наз. пределом отображения , при (в точке а), если для , , такая что для , имеет место включение . О7-8 – опр. предела по Коши. О10 (по Гейне) Точка b наз. пределом отображения , при , если сходящейся к т. a, посл-ть. сходится к точке b. Эквив. опр. 8 и 10 доказ. аналогично случаю , .

Т8 Предел отображения в точке a равен тогда и только тогда, когда , . Т9 (критер. Коши существов. предела отображения). Отображение , имеет предел в т. a тогда и только тогда, когда сущ. прокол. окр. , что и выполнено нер-во . Т10. Если отображение , имеет предел в т. a то: 1) Этот предел единственен; 2) отображение ограничено в некоторой проколотой окр-ти . Т11 Пусть , , ; и существуют 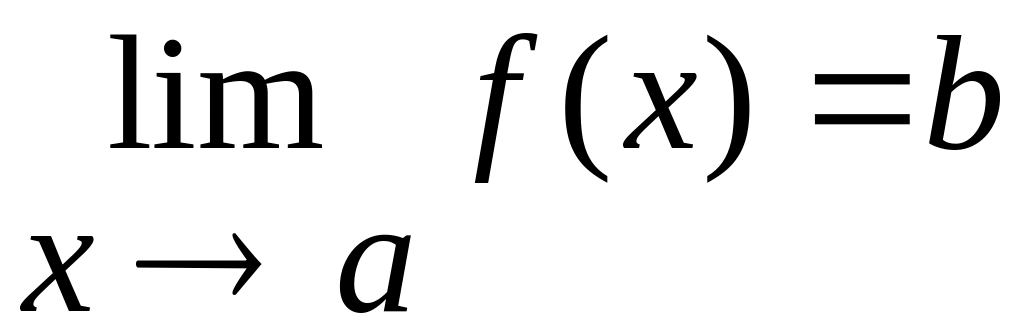; a, b – предельные точки мн-в X, соответственно. Тогда в точке a существует предел композиции отображений , причем . Т12 Если , , имеют в точке a пределы равные A и B соответсвенно, то сумма , произведение , а если то и частное имеют в этой точке пределы, причем ; ; 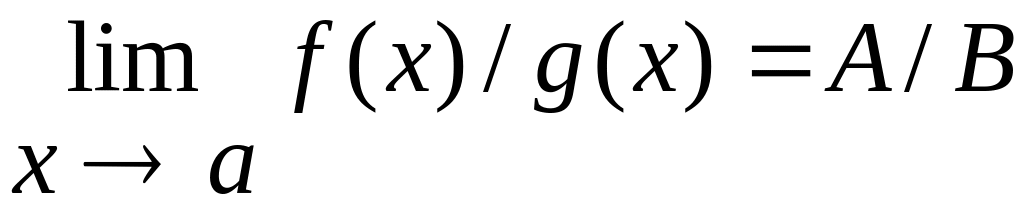. Замечание. Данные утверждения имеют место и для , если и считать суммой и скал. произведением векторов. О11. Пусть , , a – предельная точка мн-ва . Точка наз. пределом отобр. в точке a по мн-ву E, если , , что для , таких, что будет . Пишут . Пусть E={ | , , }. Тогда 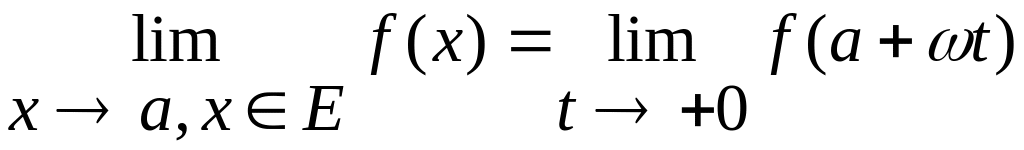. О12. Если , то он наз. пределом т. a по направлению вектора . Если имеет предел в точке , равный , то сущ. пределы равные и по любому направлению. Обратное утверждение не верно.

О13. Пусть , , a – предельная точка мн-ва . Предел вида где некоторая перестановка чисел , называется повторным пределом в точке a. Но не следует думать, что таким образом можно найти предел функции f в точке a.