1. Действительные числа. Аксиома- математическое предложение без док-ва. Рассмотрим мн-во R, кот. наз. мн-вом действ. чисел, если на нем установлены операции слож. и умнож., установл. отношение порядка, подчиненные аксиомам:

1. Аксиомы сложения.Операция подчинена аксиомам: I₁. 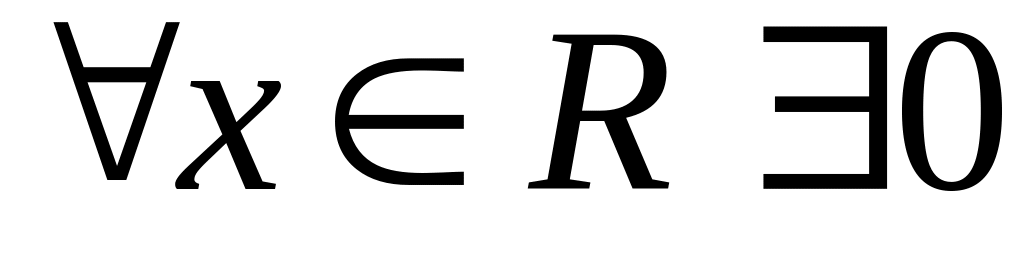, что ,0-нейтр. элемент сложения; I₂. , что , - противоп. элемент; I₃. -ассоциативность сложения; I₄. 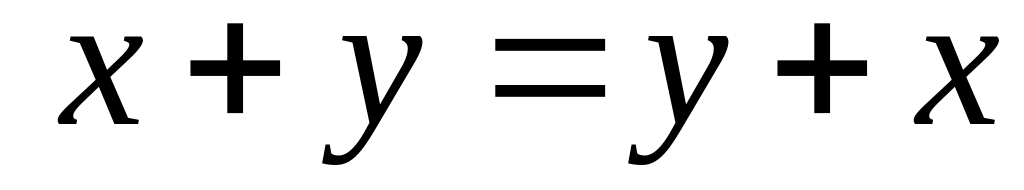-коммутативность сложения. Замечание. Мн-во с операцией, удовл. св-вам I₁- I₃ наз. группой, а если I₁- I₄ абелевой группой.

2. II. Аксиомы умножения: . II₁ , что 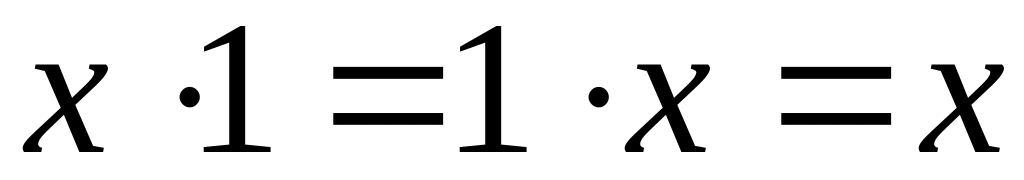, 1- нейтр. элемент умножения; II₂ 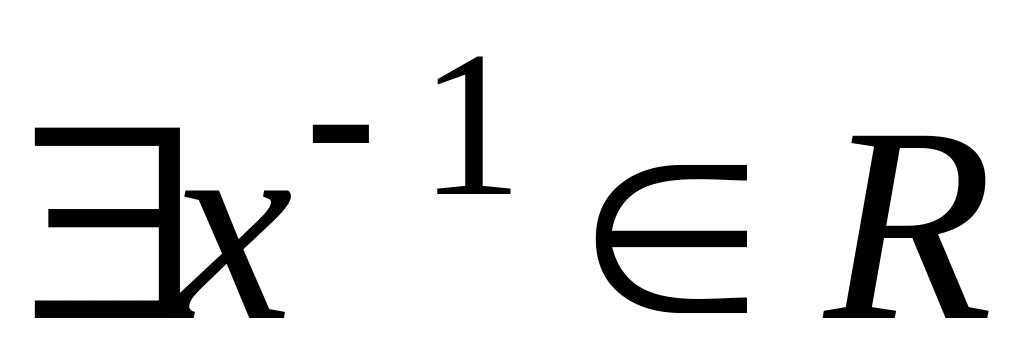,что - обратный элемент; II₃ 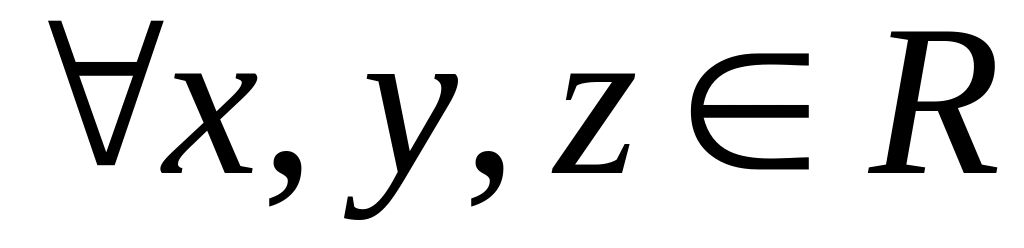; II₄ . Замечание. По отношению к операции умножения мн-во 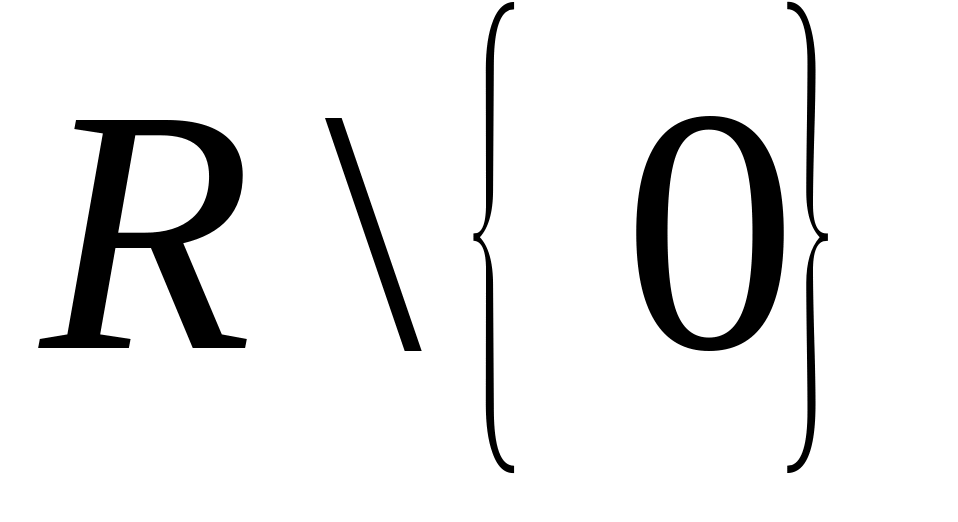- мультипликативная группа. Замечание. Если на мн-ве выполняются перечисленные аксиомы, то мн-во наз-ся алгебраическим полем.

3. III. Связь операции сложения и умножения. , .

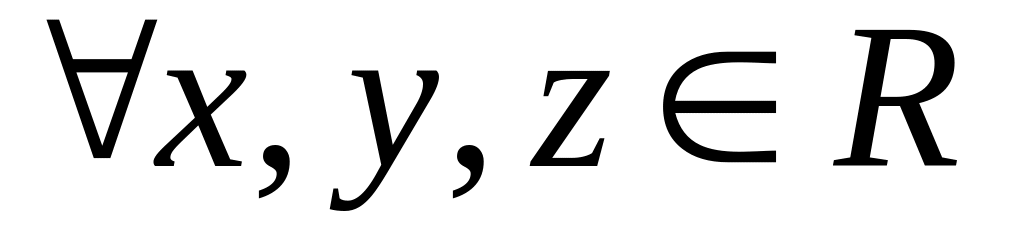4. IV Аксиомы порядка. IV₁ 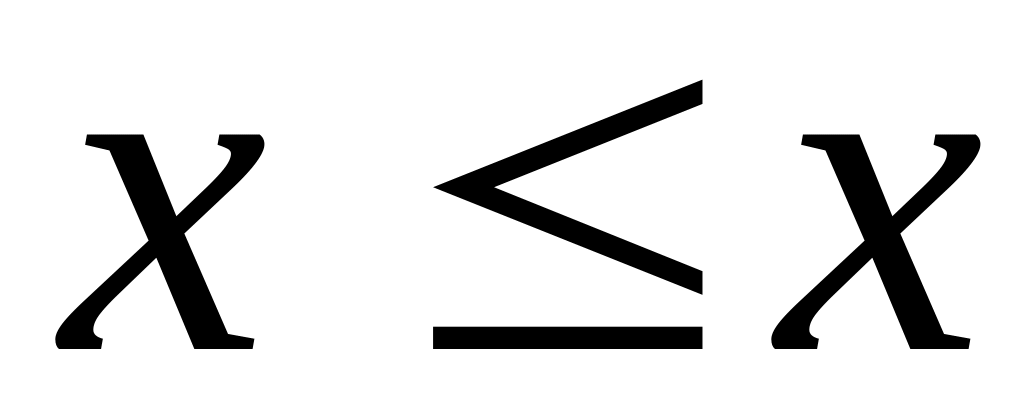-акс. рефлективности; IV₂ , ; IV₃ ; IV₄ имеет место или .

5. V.Связь операций +, * и порядка V₁. ;

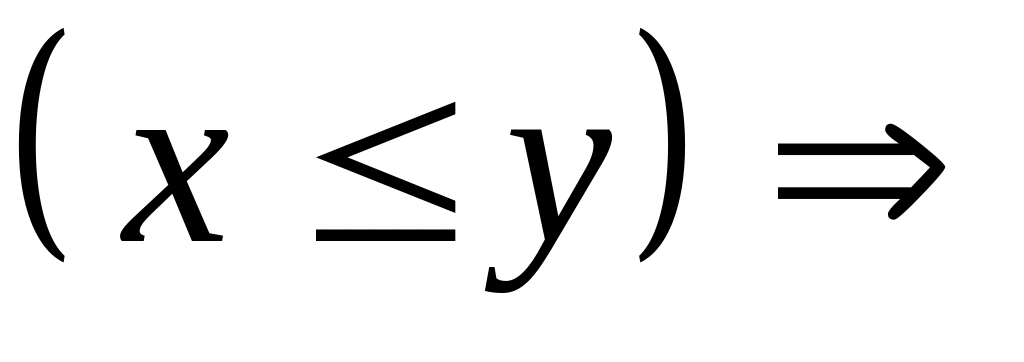
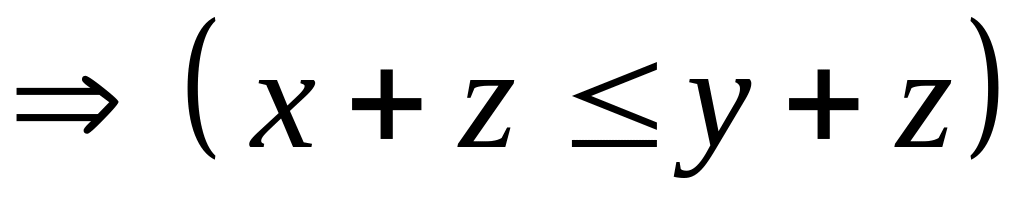V₂ .

6. VI.Аксиома полноты (непрерывности) Пусть , причем , тогда 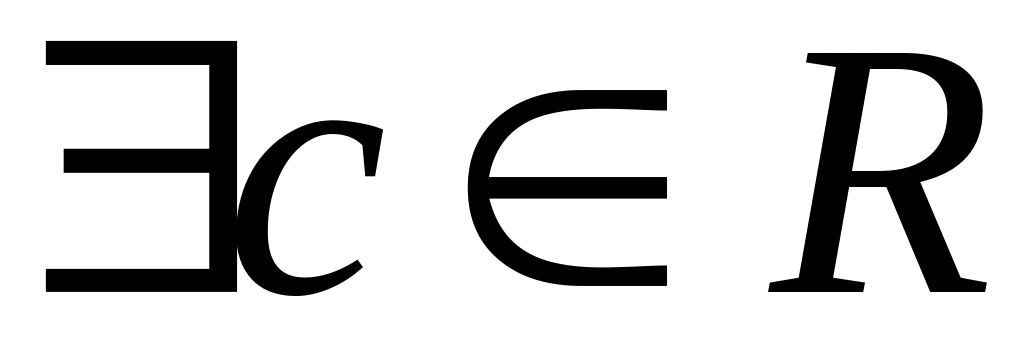, такое, что .

О1. Мн-во , , называется ограниченным сверху (снизу), если , что ( ), . О2. Множество называется ограниченным, если оно ограничено и сверху и снизу. О3 Элемент называется максимальным элементом множества (минимальным эл-том), если ( ) ,(max, min). Заметим, что макс. (миним.) элемент всегда принадлежат множеству, если они сущ. О4 Наименьшее из чисел, ограничивающих множество X сверху называют верхней точной гранью и обозн. или . Если , то выполнены условия: 1) для ; 2 , что . О5 Наибольшее из чисел, ограничивающих мн-во снизу называется нижней и обозн. или . Если , то: 1) для ; 2) , что .

Лемма1. (Принцип верхней грани). Всякое непустое ограниченное сверху числовое множество имеет единственную верхнюю грань.

2.Лемма о вложенных отрезках. Обозначим , . Тогда система -система вложенных отрезков. Лемма 2 Всякая система вложенных отрезков имеет общую точку. Если при этом , что , то такая точка единственна.

Лемма 3 о конечном покрытии. О6. Говорят, что с-ма мн-в покрывает мн-во , если любой элемент мн-ва содержится по крайней мере в одном из мн-в системы .

Лемма 3 В любой с-ме интервалов, покрывающих данный отрезок, можно выделить конечную с-му интервалов, покрывающую данный отрезок.

Лемма 4 о предельной точке. О6. Всякий интервал содержащий точку с наз. окрестностью точки. Интервалы вида наз. дельта-окр. т. а. О7. Точка наз. предельной точкой множества , если любая окрестность точки p содержит точки из отличные от p. Следствие. Если p – предельная точка мн-ва , то всякая её окрестность, содержит бесконечное множество точек из . Лемма 4 Всякое бесконечное ограниченное числовое мн-во имеет по крайней мере одну предельную точку.

2. Метрические и топологические пр-ва.

1. Метрические пр-ва.

Говорят, что на непустом неодноэлементарном мн-ве Х задана метрика , каждым двум элем-ам x,yX поставлено в соответствие неотр-ое число , причём так, что выполняются следующие условия (аксиомы метрики):

1. тогда и только тогда, когда x=y(аксиома тождественности)

2. аксиома симметрии

3. (аксиома треуг-ка)

Мн-во Х, на кот-ом задана некоторая метрика  наз-ется метр-ким пр-вом. Т.о. метрическое пр-во – пара . Элем-ты мн-ва Х наз-ются точками метрического пр-ва . Число (x,y) наз-ют расстоянием между точками x и y метрического пр-ва.

Пример:

1. , то получаемое метрическое пр-во

(R, )=R¹ – наз-ется числовой прямой (евклидовое пространство)

2. Некоторые топологические понятия метрического пр-ва.

Пусть абстрактное метр-ое пр-во, , , его подмн-ва наз. откр-ым шаром с цен-ом в т. a и радиусом r. наз. замкнутым шаром. наз. сферой.

Открытые и замкнутые шары и часто наз. открытым и соответственно замкнутым r -окрестн-ями точки а в пр-ве . Шары и сферы в пр-ве имеют следующее обозначение , , .

3. Открытые мн-ва. Натуральная топология метрического пр-ва.

Точка x подмн-ва А метрического пр-ва наз. внутренней точкой мн-ва А, если существует окрестность (точки x), которая целиком содержится в подмн-ве А ( ), r-окрестность т. x это или открытый шар или замкнутый шар .

Подмн-во А наз-ется открытым в метрическом пр-ве , если каждая его точка является внутренней.

Замечание.

Мно-во может быть открытым в одном пр-ве, но не открытым в другом. Т.о. понятие открытого мн-ва зависит от метрики пр-ва. Н-р, шар - открытое в мн-во, но не открытое в .

Т.(характерные св-ва совокупности открытых мн-в) Совокупность всех открытых в пр-ве мн-в удовлетворяет следующим условиям: 1)Ø, ; 2) объединение произвольного количества мн-в из совокупности принадлежит ; 3) пересечение конечного числа мн-в из принадлежит .

Совок-сть всех открытых в метрическом пр-ве мн-в наз-ется натуральной топологией этого пр-ва.

4. Топологические пр-ва.

Топологией на непустом мн-ве Х наз-ется произвольная совокупность его подмн-в, для которой выполняются условия (аксиомы топологии)

1. Ø, ;

2. объединение произвольного количества мн-в из совокупности принадлежит ;

3. пересечение конечного числа мн-в из принадлежит .

Мн-во Х, на котором зафиксирована некоторая топология наз-ется топологическим пр-вом и обозначается .

При этом Х - носитель топологии, а элем-ты мн-ва Х – точки ТП . Мн-во Х наз. носителем этого пр-ва. Мн-ва, которые входят в состав топологии наз. откр-ыми в топологическом пр-ве .

Сравнение топологий. Когда - топологии на мн-ве Х, говорят, что топология слабее за топологию , а топология сильнее топологии . Когда и , то наз. несравненными.

5. Замкнутые мн-ва.

Мн-во FX наз. замкнутым в ТП пр-ве , когда мн-во (его дополнение) является открытым в этом пр-ве.

Совокупность всех замкнутых мн-в в пр-ве обозначается .

Утв. Мн-во .

О. Мн-во одновременно открытое и замкнутое у пр-ве наз. открыто-замк. е нём.

Возможны следующие варианты : Мн-во А может быть :

1. открытым и замкнутым (мн-ва Х в каждом топол. пр-ве )

2. ни открытым, ни замкнутым ( (0;1] в R¹)

3. откр., но не замкнутым (мн-во (0;1) в R¹)

4. не открытым, но замкнутым ( [0;1] в R¹)

Т: Пусть совокупность всех замкнутых мн-в в пр-ве , тогда 1) Ø, ; (т.е. явл замкнутым); 2)объединение конечного числа мн-в из принадлежит ; 3)пересечение любой совок-сти замкнутых мн-в из входит в .

Т:1. Всякое открытое в мн-во есть объединение не больше, чем счётное количество числа попарно непересекающихся интервалов. T:2.Всякое замкнутое мн-во на прямой может быть получена удалением из этой прямой не более чем счётного числа попарно-непересекающихся интервалов.

6)Компактные пр-ва. Объединение множества А и всех его предельных точек называется замыканием мн. А записывается ,

О. Открытым покрытием топологического пр-ва наз-ется любая совокупность открытых в этом пространстве мн-в, объединение которых совпадает с носителем пр-ва.

О.ТП наз. компактным, если из любого открытого его покрытия можно выделить его конечное открытое покрытие, в этом случае последнее наз. подпокрытием.

Т:(критерий компактности мн-ва вRⁿ ) Для того что бы мн-во А – компактно вRⁿ необходимо и достаточно , что бы оно было одновременно замкнутым и ограниченным в Rⁿ мн-вом.

Мн-во в МП называется ограниченным, если оно целиком содержится в шаре конечного радиуса.

Св-ва компактных пр-в и мн-в:

1. Непр-ный образ компактного пр-ва есть компактное пр-во.

2. Объединение конечной сов-ти компактных мн-в в произвольном пр-ве есть компактное мн-во.

3. Пересечение любой сов-ти компактных мн-в в Rⁿ есть компактное мн-во в Rⁿ