Д ифференциальное уравнение вынужденных колебаний

1. Пружинный маятник

F_ocos(t) – внешнее гармоническое воздействие

; ;

2. К

   L

   олебательный контур

E_ocost – гармоническое воздействие ЭДС.

; q/c+RI=-L ;

В общем случае дифференциальное уравнение вынужденных колебаний:

Дифференциальное уравнение вынужденных колебаний неоднородно. Справа не ноль. Общее решение неоднородного уравнения складывается из двух, а именно: решения общего однородного уравнения и частного решения неоднородного уравнения.

Нас интересует частного решения неоднородного уравнения, которое определяет установившееся решение.

Справа гармоническая функция, слева сумма трех функций, которые тоже должны быть гармоническими с той же частотой.

Характеристики вынужденных колебаний

x(t)=Re(x(t)) x(t)=A_oe_it=A_oe_ioe_it

Осуществим подстановку:

x_/(t)=iA_oe_it x_//(t)=- ₂A_oe_it A_oe_iwt(-₂+2iw+w_o2)=f_oe_iwt

A_o= A_o= ; . Частное решение уравнения имеет вид:

x(t)= cos(wt+ )

Вынужденные колебания в системе оказались сдвинутыми по фазе по отношению к вынужденному воздействию.

х=Acos(wt+_o)

1. Частота колебаний равна частоте вынужденных колебаний

2. A(w) – амплитуда зависит от частоты воздействия. При разных частотах А(w) будет разной.

3. _о – разность фаз этого колебания и колебания вынужденного воздействия.

Амплитуда вынужденных колебаний. Явление резонанса.

1. Низкие частоты: w существеннее меньше w_о.

(на примере маятника)

При низкой частоте реакция на внешнее воздействие зависит от упругих свойств системы и от возвращающего воздействия. - статическое смещение

2. Высокие частоты: w существеннее больше w_о.

При высоких частотах определяющим является инертность системы. Чем больше инертность, тем амплитуда колебаний меньше.

3. У зависимости А(w) должен быть максимум. Амплитуда максимальна, когда минимальна.

w_о, , f_o – const, мы их зафиксировали.

w₁=0 w₂= - резонансная частота.

Когда частота воздействия равна резонансной частоте, тогда будет максимум амплитуды.

=0, при выполнении этого условия явление резонанса исчезает. Если трение велико, то резонанса не будет.

Резонанс скорости

х=Acos(wt+j_o) v= v_A=

1) низкие частоты. , т.е. движения нет.

2)

Между w и v_A должен быть максимум, следовательно резонанс скорости должен быть при любом значении трения.

V_A=

Скорость будет максимальной, когда частота вынужденного воздействия равна собственной частоте.

Резонанс скорости существует всегда при любом трении. От резонанса скорости в принципе нельзя избавиться, также существует резонанс ускорения.

В условиях малого можно считать, что все частоты приблизительно равны w₀.

Фаза вынужденных колебаний.

F = F₀cos(t), x = Acos(t+

1. =0, ₀=0

2. При произвольной частоте ₀<0, т.е. колебания которые установятся в этой системе будут отставать по фазе от колебания воздействия.

 = _ - характерная точка. В этом случае max одной системы приходится на 0 в другой и наоборот. F = F₀cos(t), x = Acos(t - /2)

Добротность и резонансные свойства системы

Резонансные свойства системы можно характеризовать добротностью.

А_рез – резонансная частота А_ст – статическое смещение

1. А_ст , когда w = 0; А_ст=

2. А_рез, когда w= w_о; А_рез=

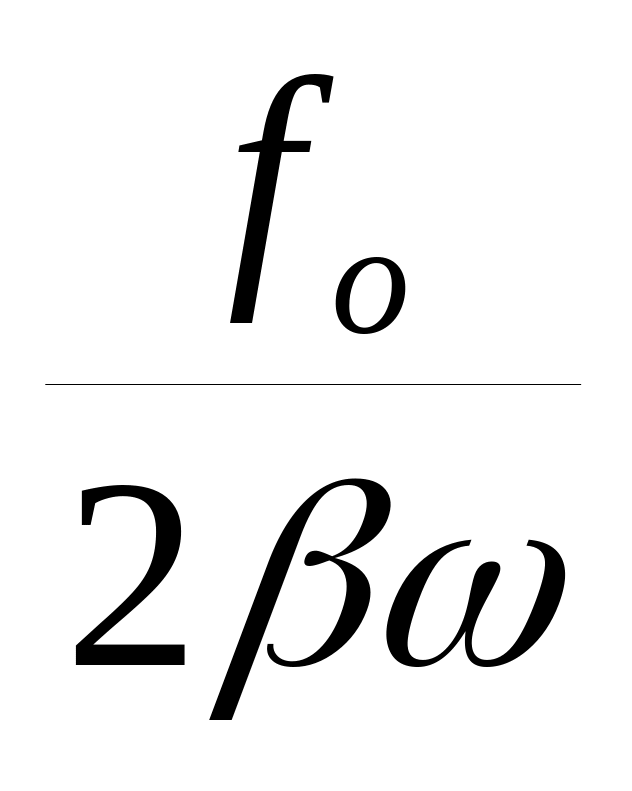
; - ширина кривой

- добротность характеризует меру ширины резонансной кривой.

Импеданс (полное сопротивление колебательной системы)

Для колебательного контура можно ввести величину импеданса:

= R+i(wL-1/(wC)) Z= =R+i(wL-1/(wC))

1) – связана с потерями энергии в контуре

2) Im( )= wL-1/(wC – реактивное сопротивление, связано с запасами энергии.

Величину импеданса можно ввести и для механической системы, например, пружинный маятник:

Z=r+i(wm-k/w)