Тема 4. Системы случайных величин
Законы распределения двумерных случайных величин. Условные распределения двух случайных величин. Числовые характеристики двумерных законов распределения. Корреляция. Числовые характеристики n-мерных случайных величин. Функциональные преобразования двумерных плотностей вероятностей. Гамма-распределение. Распределение хи-квадрат. Двумерное нормальное распределение.
Сначала изучите материал, изложенный в главе 4 [1]. Затем ответьте на вопросы и выполните задания для самопроверки. Внимательно разберите решения приведенных примеров. Решите задачи для самостоятельного решения. Из контрольной работы выполните 5-е задание своего варианта.
При изучении материала обратите особое внимание на следующее.
Как и для одномерных случайных величин, на законы распределения многомерных случайных величин налагается условие нормировки.
Одномерные функции распределения и плотности вероятности могут быть найдены через двумерные.
Условный закон распределения – закон распределения одной случайной величины при условии, что другая случайная величина приняла определенное значение. Для нахождения условной плотности вероятности случайной величины X, образующей со случайной величиной Y двумерную систему, можно воспользоваться формулой:
.
Если совместный закон распределения (плотность вероятности) системы случайных величин можно представить в виде произведения законов распределения каждой случайной величины, то такие случайные величины являются независимыми.
Основными числовыми характеристиками системы случайных величин являются математические ожидания и дисперсии каждой случайной величины, а также корреляционные моменты (или коэффициенты корреляции) между каждой парой случайных величин. Если система состоит из двух случайных величин X и Y, то имеем математические ожидания
и
,
дисперсии
и
и корреляционный момент
.Коэффициент корреляции между двумя случайными величинами X и Y определяет степень линейной вероятностной зависимости между этими величинами.
Независимые случайные величины всегда некоррелированы, зависимые – могут быть как коррелированными, так и некоррелированными.
При нахождении дисперсии или суммы случайных величин необходимо учитывать корреляцию между ними.
Композиция законов распределения – задача нахождения плотности вероятности суммы нескольких независимых случайных величин по известным законам распределения слагаемых. Эта задача может быть решена путем последовательного вычисления интегралов свертки или с помощью аппарата характеристических функций.
Распределение
(хи-квадрат)
описывает распределение суммы квадратов
k
независимых случайных величин, каждая
из которых имеет стандартное нормальное
распределение. Число k
называется числом степеней свободы
распределения
.
Вопросы и задания для самопроверки
Как выглядит закон распределения дискретной двумерной случайной величины, представленный таблицей?
Как, зная закон распределения двумерной случайной величины (X,Y), найти законы распределения случайных величин X и Y?
Какими свойствами обладает функция распределения двумерной случайной величины?
Какими свойствами обладает плотность вероятности двумерной случайной величины?
Как, зная двумерную функцию распределения, найти одномерную функцию распределения.
Какое условие является необходимым и достаточным для того, чтобы две дискретные величины были независимыми?
Как проверить независимость двух непрерывных случайных величин?
Какими числовыми характеристиками описываются двумерные случайные величины?
Двумерная случайная величина характеризуется двумя математическими ожиданиями или одним?
Дайте определение корреляционного момента двумерной случайной величины. Что этот момент характеризует?
Что такое коэффициент корреляции? В каком диапазоне лежат его значения?
Если коэффициент корреляции равен нулю, означает ли это, что случайные величины независимы?
Чему равно математическое ожидание произведения двух зависимых случайных величин?
Чему равны дисперсии суммы и разности двух зависимых случайных величин?
Какими основными числовыми характеристиками описываются n-мерные случайные величины?
Напишите формулу для интеграла свертки двух плотностей вероятностей. Что эта формула позволяет находить?
Распределение какой случайной величины описывается гамма-распределением?
Что называют случайной величиной
?
Какое распределение она имеет?Какие две случайные величины называются совместно нормальными?
Будут ли две совместно нормальные случайные величины независимыми, если они некоррелированы?
Примеры решения задач
Пример 1. Закон распределения двумерной дискретной случайной величины (X,Y) задан таблицей
|
|
|
|
0,10 |
0,15 |
|
0,15 |
0,25 |
|
0,20 |
0,15 |
Найти: 1) законы
распределения случайных величин X
и Y; 2) условный
закон распределения случайной величины
X при условии, что
величина Y приняла
значение
;
3) условный закон распределения случайной
величины Y при условии,
что величина X приняла
значение
;
Решение:
1. Для нахождения безусловных законов распределения случайных величин X и Y воспользуемся формулами:
,
.
Имеем:
Таким образом, закон распределения случайной величины X имеет вид:
|
|
|
|
|
|
|||||
|
|
0,45 |
|
0,55 |
|
|||||
Для случайной величины Y по аналогии получим:
Закон распределения имеет вид:
|
|
|
|
|
|
|
|
|
0,25 |
|
0,40 |
|
0,35 |
2. Условный закон
распределения случайной величины X
при
определяется совокупностью условных
вероятностей
и
,
которые по теореме умножения вероятностей
равны:
Этот закон имеет вид:
|
|
|
|
|
|
|
|
2/5 |
|
3/5 |
|
|
|
||||
3. Условный закон
распределения случайной величины Y
при
находится аналогично:
Этот закон имеет вид:
|
|
|
|
|
|
|
|
|
0,25 |
|
0,40 |
|
0,35 |
Пример 2. Совместная функция распределения случайных величин X и Y имеет вид:
,
Определить: 1) совместную плотность вероятности случайной величины (X,Y); одномерные плотности вероятности случайных величин X и Y; 3) являются ли случайные величины независимыми.
Решение.
По определению
2.
3. Случайные величины X и Y независимы, так как их совместная плотность вероятности представляется в виде произведения одномерных плотностей вероятностей случайных величин.
Пример 3. Двумерная случайная величина (X,Y) распределена равномерно внутри круга радиусом а.
Записать выражение
для плотности вероятности p(x,y).
Найти условные плотности вероятности
и
.
Ответить на вопрос: зависимы ли cлучайные
величины X
и
Y?
Решение. Значение плотности вероятности внутри круга находится из условия нормировки:
.
Значит
и
,
.
Находим одномерные плотности вероятности:
;
, 
.
Условные плотности вероятности:
;
.
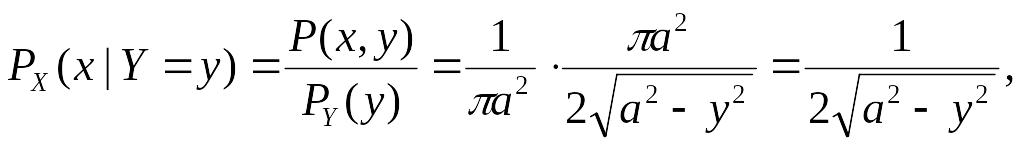
Случайные величины X и Y зависимы, так как их совместная плотность P(X,Y) нельзя представить в виде произведения одномерных плотностей вероятностей.
Пример 4. Совместная плотность вероятности случайных величин X и Y имеет вид:
На стр. 69 [1] было показано, что случайные величины зависимы. Являются ли они коррелированными? Найти коэффициент корреляции.
Решение. Находим одномерные плотности вероятности:
Находим математические ожидания:
Корреляционный момент по определению:
или
Находим M[XY]:
Таким образом, случайные величины коррелированны.
Чтобы найти коэффициент корреляции, необходимо найти дисперсии случайных величин.
Аналогично
Коэффициент корреляции
Пример 5.
Случайная величина
распределена равномерно в интервале
от 0 до 1, случайная величина
имеет
экспоненциальное распределение с
параметром равным 1.
Найти плотность
вероятности случайной величины
.
Решение. Плотности вероятности случайных величин и и их графики имеют следующий вид:
Плотность вероятности
случайной величины
определяется
формулой композиции (интегралом свертки
плотностей вероятностей):
Функция
представляет собой функцию, являющуюся
зеркальным отражением функции
относительно
оси ординат и сдвинутую по оси абсцисс
на величину y.
Для вычисления
интеграла свертки при текущем значении
параметра y
необходимо проинтегрировать произведение
плотностей вероятностей
и
по области перекрытия этих функций:
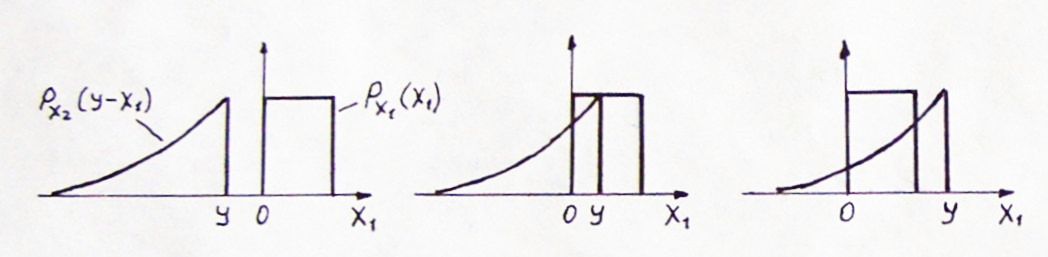
При y<0
значения
,
поскольку перекрытие функций отсутствует.
При значениях y,
лежащих в пределах от 0 до 1,
Когда y>1,
Таким образом,
График плотности вероятности случайной величины имеет следующий вид:
Задачи для самостоятельного решения
Задача 1. Дискретная случайная величина (X,Y) задана таблицей
X
|
2 |
5 |
8 |
0,4 |
0,15 |
0,30 |
0,35 |
0.8 |
0,05 |
0,12 |
0,03 |
Y
Найти условный закон распределения случайной величины X, при Y=0,8.
Ответ:
X |
|
2 |
|
5 |
|
8 |
|
|
0,25 |
|
0,6 |
|
0,15 |
Задача 2.
Независимые случайные величины X
и
Y
распределены по нормальным законам с
параметром
,
,
,
.
Написать выражение для плотности вероятности P(X,Y) системы случайных величин.
Ответ:
,
Задача 3.
Найти плотность вероятности суммы двух
случайных величин
,
каждая из которых распределена равномерно
на интервале (0,b).
Ответ:
