Ргз №1 по теме " Приложения диф. Исчисления функций одной переменной "

Вариант 9

Задача 1

Найти наибольшее и наименьшее значения функции на замкнутом промежутке, построив ее график на этом промежутке, если , .

Задача 2

Провести полное исследование свойств следующих функции и построить их графики:

1) ; 2) ; 3) ; 4) .

Задача 3 (Берман, №1244)

Бревно длиной 20 м имеет форму усеченного конуса, диаметры оснований которого равны соответственно 2 м и 1 м. Требуется вырубить из бревна балку с квадратным поперечным сечением, ось которой совпадала бы с осью бревна и объем которой был бы наибольшим. Каковы должны быть размеры балки?

Задача 4

Используя равенство , вычислить приближенно .

Задача 5 (Берман, №820)

Тело массой 3 кг движется прямолинейно по закону ; s выражено в сантиметрах, t – в секундах. Определить кинетическую энергию тела через 5 с после начала движения.

Задача 6

Д ан график функции :

Найти:

1) значение ;

2) ;

3) точки экстремумов;

4) значения , для которых выполняются три условия , , ;

5) значения , для которых ;

6) уравнения асимптот;

7) численное значение ;

8) промежутки знакопостоянства .

Спец. 230100.62 “ИВТ(б)”

дисц. Матем. анализ

Ргз №1 по теме " Приложения диф. Исчисления функций одной переменной "

Вариант 10

Задача 1

Найти наибольшее и наименьшее значения функции на замкнутом промежутке, построив ее график на этом промежутке, если , .

Задача 2

Провести полное исследование свойств следующих функции и построить их графики:

1) ; 2) ; 3) ; 4) .

Задача 3 (Берман, №1247)

Прямо над центром круглой площадки фиксированного радиуса R нужно повесить фонарь. На какой высоте нужно это сделать, чтобы он наилучшим образом освещал дорожку, которой обведена площадка. (Степень освещения некоторой площадки прямо пропорциональна косинусу угла падения лучей и обратно пропорциональна квадрату расстояния от источника света.)

Задача 4

Используя равенство , вычислить приближенно .

Задача 5 (Берман, №1086)

Точка движется прямолинейно так, что скорость ее изменяется пропорционально квадратному корню из пройденного пути. Показать, что движение происходит под действием постоянной силы.

Задача 6

Д ан график функции :

Н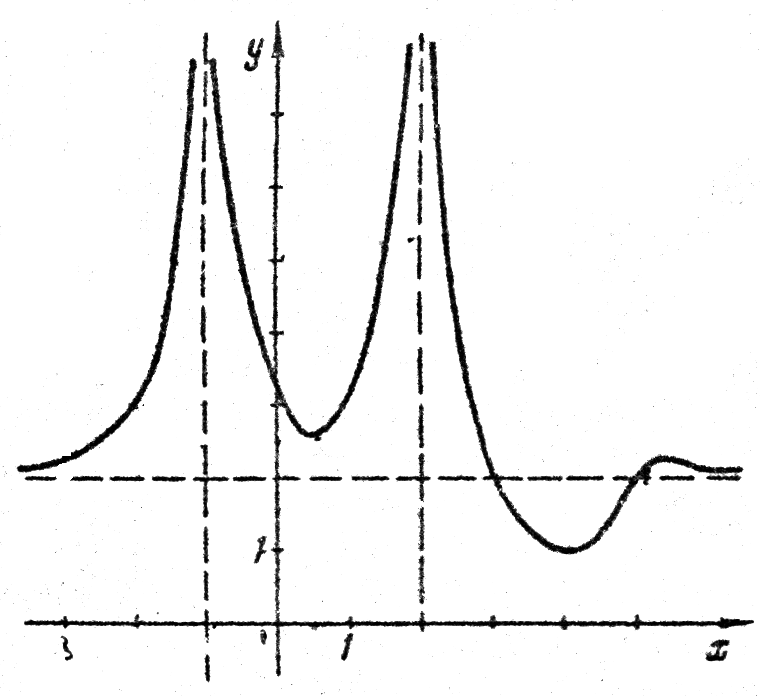 айти:

1) значение ;

2) ;

3) точки экстремумов;

4) значения , для которых одновременно

выполняются условия , , ;

5) значения , для которых ;

6) уравнения асимптот;

7) численное значение ;

8) промежутки знакопостоянства .

Спец. 230100.62 “ИВТ(б)”

дисц. Матем. анализ

Ргз №1 по теме " Приложения диф. Исчисления функций одной переменной "

Вариант 11

Задача 1

Найти наибольшее и наименьшее значения функции на замкнутом промежутке, построив ее график на этом промежутке, если , .

Задача 2

Провести полное исследование свойств следующих функции и построить их графики:

1) ; 2) ; 3) ; 4) .

Задача 3 (Берман, №1235)

Какова должна быть высота конуса, вписанного в шар фиксированного радиуса R, для того чтобы его боковая поверхность была наибольшей?

Задача 4

Используя равенство , вычислить приближенно .

З адача 5 (Берман, №1084)

Тяжелую балку длиной 13 м спускают на землю так, что нижний конец прикреплен к вагонетке, а верхний удерживается канатом, намотанным на ворот. Канат сматывается со скоростью 2 м/мин. С каким ускорением откатывается вагонетка в момент, когда она находится на расстоянии 5 м от точки О (рис.1)?

Задача 6

Д ан график функции :

Н

рис.1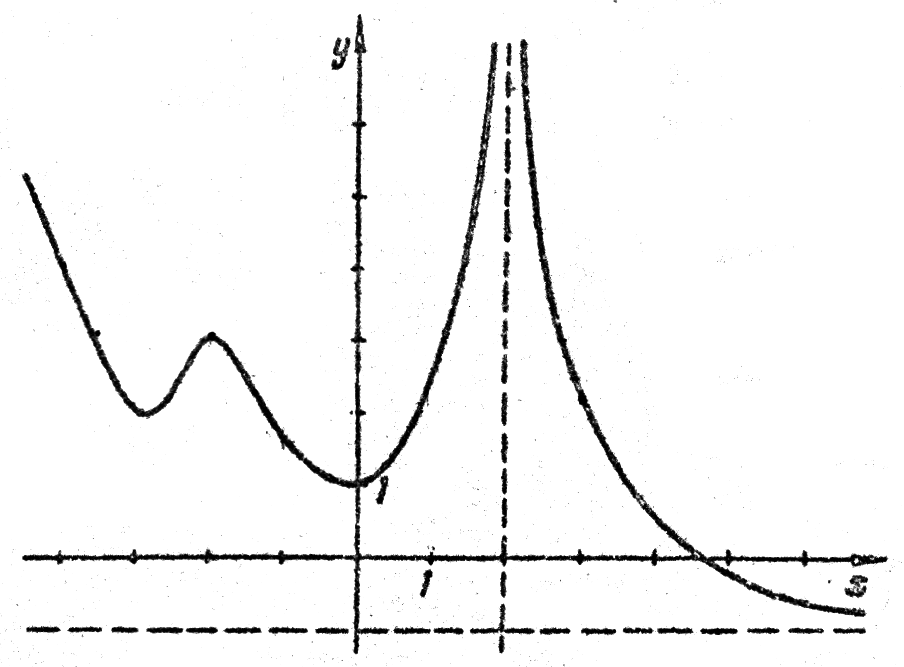

айти:

1) значение ;

2) ;

3) экстремумы функции;

4) значения , для которых выполняются три условия , и ;

5) значения , для которых ;

6) уравнения асимптот;

7) значение ;

8) промежутки знакопостоянства .

Спец. 230100.62 “ИВТ(б)”

дисц. Матем. анализ