
- •«Мурманский государственный технический университет»
- •Методические указания к выполнению расчетно-графического задания
- •Оглавление
- •1. Общие организационно-методические указания
- •2. Задание, план выполнения, требования к оформлению
- •Содержание задач каждого варианта:
- •Общие требования к оформлению ргз:
- •План выполнения ргз:
- •3. Список рекомендуемых источников
- •Задача 2
- •Задача 3
- •Задача 4
- •Задача 5
- •Задача 6
- •Приложение а. Образец оформления титульного листа
- •Расчетно-графическое задание №1
- •Приложение б. Варианты заданий
- •Ргз №1 по теме " Приложения диф. Исчисления функций одной переменной "
- •Ргз №1 по теме " Приложения диф. Исчисления функций одной переменной "
- •Ргз №1 по теме " Приложения диф. Исчисления функций одной переменной "
- •Ргз №1 по теме " Приложения диф. Исчисления функций одной переменной "
- •Ргз №1 по теме " Приложения диф. Исчисления функций одной переменной "
- •Ргз №1 по теме " Приложения диф. Исчисления функций одной переменной "
- •Ргз №1 по теме " Приложения диф. Исчисления функций одной переменной "
- •Ргз №1 по теме " Приложения диф. Исчисления функций одной переменной "
- •Ргз №1 по теме " Приложения диф. Исчисления функций одной переменной "
- •Ргз №1 по теме " Приложения диф. Исчисления функций одной переменной "
- •Ргз №1 по теме " Приложения диф. Исчисления функций одной переменной "
- •Ргз №1 по теме " Приложения диф. Исчисления функций одной переменной "
- •Ргз №1 по теме " Приложения диф. Исчисления функций одной переменной "
- •Ргз №1 по теме " Приложения диф. Исчисления функций одной переменной "
- •Ргз №1 по теме " Приложения диф. Исчисления функций одной переменной "
- •Ргз №1 по теме " Приложения диф. Исчисления функций одной переменной "
- •Ргз №1 по теме " Приложения диф. Исчисления функций одной переменной "
- •Ргз №1 по теме " Приложения диф. Исчисления функций одной переменной "
- •Ргз №1 по теме " Приложения диф. Исчисления функций одной переменной "
- •Ргз №1 по теме " Приложения диф. Исчисления функций одной переменной "
- •Ргз №1 по теме " Приложения диф. Исчисления функций одной переменной "
- •Ргз №1 по теме " Приложения диф. Исчисления функций одной переменной "
- •Ргз №1 по теме " Приложения диф. Исчисления функций одной переменной "
- •Ргз №1 по теме " Приложения диф. Исчисления функций одной переменной "
Задача 2
Провести полное исследование свойств следующих функций и построить их графики:
1) ; 2) ; 3) ; 4) .
Решение
ООФ:
 ;
;
нули функции и промежутки знакопостоянства:
![]() ;
;
![]() ООФ
ООФ
![]() нулей функции нет;
нулей функции нет;
![]() на всем промежутке существования функии
;
на всем промежутке существования функии
;
непрерывность, точки разрыва, вертикальные асимптоты:
функция непрерывна на промежутке
![]() так
как является элементарной,
так
как является элементарной,
следовательно непрерывной на своей ООФ;
проверим наличие вертикальной асимптоты
на границе ООФ, то есть при
![]() :
:
![]() – односторонняя (левосторонняя)
вертикальная асимптота графика функции;
– односторонняя (левосторонняя)
вертикальная асимптота графика функции;
четность, периодичность:
свойством четности данная функция обладать не может, так как её ООФ не является симметричной относительно нуля; следовательно, функция не является ни четной, ни нечетной;
функция не является периодической;
монотонность и экстремумы:
![]() ;
;
![]() ,
т.е.
,
т.е.
![]() –
стационарная точка;
–
стационарная точка;

достаточные условия монотонности и экстремумов:
знаки
![]()
монотонность
![]()
вычисляем экстремум функции:

![]() ;
;
функция убывает
на промежутке
![]() и
и
возрастает на
промежутке
![]() ;
;
вогнутость, выпуклость, точки перегиба:
![]() ;
;
точки, подозрительные на перегиб:
![]()
![]()
![]() ;
;

достаточные условия выпуклости, вогнутости, точек перегиба:
знаки
![]()
выпуклость/вогнутость
вычисляем ординату точки перегиба:
![]() ;
;
точка перегиба
 ;
график функции является вогнутым на
промежутке
;
график функции является вогнутым на
промежутке
![]() и выпуклым на промежутке
и выпуклым на промежутке
![]() ;
;
наклонные (горизонтальные) асимптоты:
если график имеет наклонную асимптоту,
то её уравнение
![]() ,
где
,
где
![]() ,
,
![]() ;
;
вычисляем значения k и b для исследуемой функции:

так как
![]() ,
то
,
то
![]()
![]() наклонных
асимптот нет;
наклонных
асимптот нет;
дополнительные точки графика:
![]()
![]() .
.
О
 твет
1: график функции
твет
1: график функции
сводная таблица свойств функции :
x |
(0;1) |
1 |
(1;3) |
3 |
(3; |
|
– |
0 |
+ |
+ |
+ |
|
+ |
+ |
+ |
0 |
– |
|
|
min y=2 |
|
перегиб
y |
|
односторонняя
вертикальная асимптота x
= 0 (при![]() ).
).
ООФ:

ОЗФ, нули функции, промежутки знакопостоянства:
 нулей
функции нет;
при
нулей
функции нет;
при
 ;
;
непрерывность, точки разрыва, вертикальные асимптоты:
функция непрерывна на своей ООФ, так как является элементарной нет точек разрыва нет вертикальных асимптот;
четность, периодичность:
функция может обладать свойством четности, так как её ООФ симметрична относительно нуля;
![]() –
функция ни четная, ни нечетная;
–
функция ни четная, ни нечетная;
функция не является периодической;
монотонность, точки экстремумов:
![]() ;
;
необходимое условие экстремумов:
![]()
![]()
![]() –это
стационарные точки;
–это
стационарные точки;
д остаточные
условия монотонности и экстремумов:
остаточные
условия монотонности и экстремумов:
знаки
м онотонноть
онотонноть
экстремумы y:

![]() на промежутке
на промежутке
![]() ;
;
![]() на
промежутке
на
промежутке
![]() ;
;
вогнутость, выпуклость, точки перегиба:
![]()
необходимое условие перегибов:
![]() –
–
это точки, подозрительные на перегиб;
достаточные условия выпуклости, вогнутости, точек перегиба:
з
 наки
наки
выпуклость/вогнутость
ординаты точек перегиба:

график функции имеет две точки перегиба
![]() ,
является вогнутым на промежутках
,
является вогнутым на промежутках
![]() и является выпуклым на промежутке
и является выпуклым на промежутке
![]() ;
;
наклонные и горизонтальные асимптоты:
если график имеет наклонную асимптоту,
то её уравнение
![]() где
где
, ;
так как
![]() при
при
![]() ,
а
,
а
![]() при
при
![]() ,
то для данной функции нужно отдельно
рассматривать пределы при
и при
:
,
то для данной функции нужно отдельно
рассматривать пределы при
и при
:
 при
асимптот нет;
при
асимптот нет;

 так
как
,
то
так
как
,
то
![]()
![]() ;
;
прямая![]() является горизонтальной асимптотой,
но только при
;
является горизонтальной асимптотой,
но только при
;
дополнительные точки графика:
![]()
![]() ;
;
Ответ 2: график функции

A (0,6; 1,2)
B (2; 1,54)
C (3,4; 1,4)
сводная таблица свойств функции :
х |
|
0 |
|
0,6 |
|
2 |
(2; 3,4) |
3,4 |
|
|
– |
0 |
+ |
+ |
+ |
0 |
– |
– |
– |
|
+ |
+ |
+ |
0 |
– |
– |
– |
0 |
+ |
|
|
min y=1 |
|
перегиб
|
|
max
|
|
перегиб
|
|
горизонтальная асимптота
y=1 при
![]()
ООФ:
непрерывность, точки разрыва, вертикальные асимптоты:
функция непрерывна на всей ООФ, т.е. при
![]()
![]() ,
так как является элементарной
точек разрыва нет и вертикальных
асимптот нет;
,
так как является элементарной
точек разрыва нет и вертикальных
асимптот нет;
четность, нечетность, периодичность:
функция может обладать свойством четности, так как её ООФ симметрична относительно нуля;
![]() функция
не является ни четной, ни нечетной;
функция
не является ни четной, ни нечетной;
функция не является периодической;

нули функции и промежутки знакопостоянства:
y = 0![]()
![]() или
или
![]()

знаки
монотонность, точки экстремумов:
![]() ;
;
необходимое условие экстремумов:

функция имеет две критические точки
![]() и
и
![]() ,
причем, точка x2
является подозрительной на острый
экстремум;
,
причем, точка x2
является подозрительной на острый
экстремум;
д остаточные
условия монотонности и экстремумов:
остаточные
условия монотонности и экстремумов:
знаки
монотонноть
![]()

![]()
![]()
![]() ;
;
вогнутость, выпуклость, точки перегиба:
 ;
;
необходимые условия перегиба:
![]()

функция имеет 2 точки, подозрительные на перегиб;
достаточные условия перегиба:

знаки
выпуклость/вогнутость
ордината точки перегиба:
![]() ;
;
график функции имеет одну точку перегиба
![]() ,
является выпуклым на промежутке
,
является выпуклым на промежутке
![]() и является вогнутым на промежутке
и является вогнутым на промежутке
![]() ;
;
наклонные и горизонтальные асимптоты:
если график имеет наклонную асимптоту,
то её уравнение
![]() где
где

наклонных асимптот нет;
дополнительные точки графика:
![]() ;
; ![]() .
.
Ответ 3: график функции
![]()

A(-0,2; -0,41)
B(0,4; -0,324)
сводная таблица свойств функции :
х |
|
-0,2 |
|
0 |
|
0,4 |
|
|
+ |
+ |
+ |
не
|
– |
0 |
+ |
|
– |
0 |
+ |
не |
+ |
+ |
+ |
|
|
перегиб y = –0,41 |
|
0 |
|
min y = –0,324 |
|
ассимптот у графика нет.
ООФ:
 ,
то есть
,
то есть
 ;
;нули функции, промежутки знакопостоянства:
![]()
![]()
![]() нулей функции нет;
нулей функции нет;
![]()
 на промежутке
на промежутке
![]() ,
на промежутке
,
на промежутке
![]() ;
;
непрерывность, точки разрыва, вертикальные асимптоты:
функция имеет точку разрыва
,
так как эта точка не принадлежит ООФ,
но её окрестность входит в ООФ; чтобы
узнать поведение функции в окрестности
точки разрыва
,
нужно вычислить односторонние пределы
функции при
![]() :
:

- точка бесконечного разрыва (разрыв второго рода),
прямая является вертикальной асимптотой графика функции;
четность, периодичность:
ООФ не является симметричной относительно нуля, поэтому функция не может обладать свойством четности/нечетности, следовательно, функция не является ни четной, ни нечетной; также функция не является периодической;
монотонность, точки экстремумов:
![]() ;
;
необходимое условие экстремумов:
![]()
![]() ;
;
![]() не существует при
,
но эта точка не входит в ООФ, поэтому
не является подозрительной на экстремум;
не существует при
,
но эта точка не входит в ООФ, поэтому
не является подозрительной на экстремум;
д остаточные
условия монотонности и экстремумов:
остаточные
условия монотонности и экстремумов:
знаки
монотонноть
![]()

в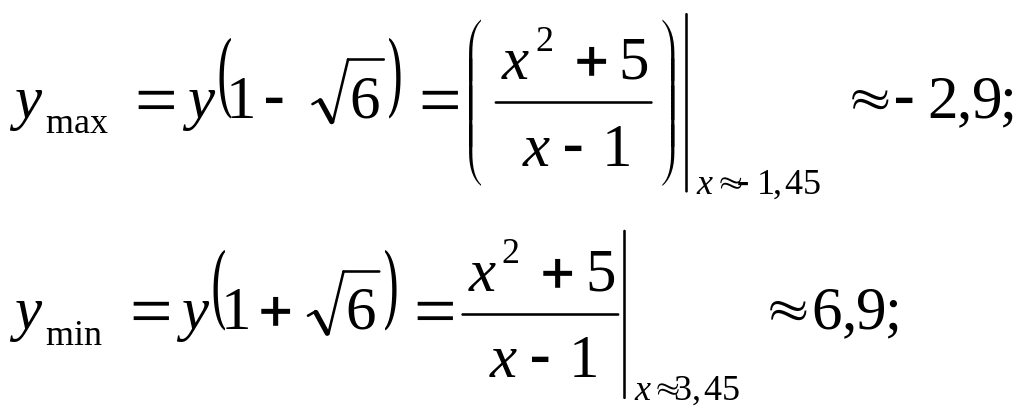 ычисляем
экстремумы функции:
ычисляем
экстремумы функции:
данная функция возрастает на промежутках
![]() и
и
![]() и
и
убывает на промежутках
![]() и
и
![]() ,
,
имеет два экстремума:
![]()
вогнутость/выпуклость, точки перегиба:

необходимое условие перегиба:
![]() нет точек перегиба;
нет точек перегиба;
![]()
 не существует при
,
но эта точка не входит в ООФ, поэтому в
ней перегиб быть не может;
не существует при
,
но эта точка не входит в ООФ, поэтому в
ней перегиб быть не может;
д остаточное
условие выпуклости/вогнутости:
остаточное
условие выпуклости/вогнутости:
знаки
выпуклость/вогнутость
график функции является выпуклым на
промежутке
![]() и является вогнутым на промежутке
и является вогнутым на промежутке
![]() ;
;
наклонные и горизонтальные асимптоты:
где , ;
Вычисляем числа k и b для данной функции:
 ;
;
 ;
;
по найденным числам k
и b делаем вывод,
что![]() – уравнение наклонной асимптоты.
– уравнение наклонной асимптоты.
Ответ 4: график функции
![]()

А(3,45; 6,9)
В(1,45; -2,9)
сводная таблица свойств функции :
х |
|
-1,45 |
(-1,45; 1) |
1 |
(1; 3,45) |
3,45 |
|
|
+ |
0 |
– |
|
– |
0 |
+ |
|
– |
– |
– |
|
+ |
+ |
+ |
|
|
max
|
|
|
|
min
|
|
– уравнение наклонной асимптоты,
x = 1 – уравнение вертикальной асимптоты.






