19

Министерство образования и науки Российской Федерации

Государственное образовательное учреждение

высшего профессионального образования

«Брянская государственная инженерно-технологическая академия»

Кафедра математики

“Алгоритмы и их виды”

Методические указания и задания к расчетно-графической работе для студентов всех направлений подготовки бакалавров очной формы обучения

Брянск 2012

Министерство образования и науки Российской Федерации

Государственное образовательное учреждение

высшего профессионального образования

«Брянская государственная инженерно-технологическая академия»

Кафедра математики

УТВЕРЖДЕНЫ

научно-методическим

советом академии

Протокол № ____

oт “____”___________2012 г.

“Алгоритмы и их виды ”

Методические указания и задания к расчетно-графической работе для студентов всех направлений подготовки бакалавров очной формы обучения

Брянск 2012

Авторы:

Камозина Олеся Владимировна

Часова Наталья Александровна

Рецензент: профессор каф. физики, к. физ.-мат. наук Евтюхов К. Н.

Рассмотрены УМК МТФ

Протокол № от

Введение: интуитивное понятие алгоритма. Свойства алгоритма. Вычислимые функции

Под алгоритмом (в интуитивном смысле) понимается упорядоченная система указаний, позволяющая за конечное число шагов получить однозначное решение каждой задачи данного класса.

Примеры. 1) алгоритм решения задач по теме «Формула полной вероятности»;

2) алгоритм решения квадратного уравнения;

3) любая компьютерная программа.

Простейшие алгоритмы возникли еще в глубокой древности. Узбекский математик аль-Хорезми (IX век до нашей эры) разработал правила четырех арифметических действий над числами в десятичной системе счисления. С его именем и связано слово «алгоритм».

Свойства алгоритма:

1. наличие начальных данных, к которым применяются указания;

2. дискретность алгоритма (необходимый для вычислений интервал времени разбит на промежутки - шаги);

3. определенность алгоритма (результат не зависит от того, кто выполняет алгоритм);

4. элементарность алгоритма (каждое действие выполняется элементарно);

5. массовость алгоритма (алгоритм служит не для решения одной конкретной задачи, а для решения целого класса задач. Процедуру решения одной индивидуальной задачи не называют алгоритмом).

Не для всех задач удается найти алгоритм решения.

Пример. Уравнение , где P – многочлен произвольной степени с целыми коэффициентами, не разрешено в целых числах (Юрий Матиясевич, аспирант Ленинградского университета, 1970). Это доказательство оказалось возможным, благодаря введению точного математического определения алгоритма. Существует несколько вариантов таких определений, которые трактуются как самостоятельные математические понятия. Каждое из них имеет свое название: рекурсивные функции, нормальные алгоритмы Маркова, машины Тьюринга.

Уточним понятие алгоритма с помощью функции.

Вычислимая функция - это функция, для которой существует вычисляющий ее значения алгоритм. По сути, алгоритму решения задачи сопоставляется вычислимая функция, дающая ответ на вопрос задачи.

Теоретический материал

1. Рекурсивные функции

Функция, определенная и со значениями на подмножествах множества ℕ{0}, называется арифметической.

Простейшие (базисные) функции:

1. 0(x)=0, ℕ{0} – нуль функция;

2. , ℕ{0} – функция следования;

3. ℕ{0} – функция выделения аргумента.

Эти функции вычислимы и на их основе можно построить более сложные вычислимые функции с помощью операторов (правил).

1. Оператор суперпозиции

Пусть h(x₁,…,x_n) – n-местная функция (зависит от n переменных), g₁(y₁,…,y_m), g₂(y₁,…,y_m), …, g_n(y₁,…,y_m) – m-местные функции. Тогда функция f(y₁,…,y_m)=h(g₁(y₁,…,y_m),g₂(y₁,…,y_m),…,g_n(y₁,…,y_m)) – функция, полученная с помощью оператора суперпозиции из функций h, g₁, g₂, …, g_m.

Пример. Пусть h(x₁,x₂)=2x₁+3x₂, g₁(y₁,y₂,y₃)=y₁+2y₂+5y₃, g₂(y₁,y₂,y₃)=2y₁+3y₃. Тогда f(y₁,y₂,y₃)=2(y₁+2y₂+5y₃)+3(2y₁+3y₃)=8y₁+4y₂+19y₃ – суперпозиция функций h, g₁, g₂.

Определим с помощью оператора суперпозиции нуль функцию и константу от n переменных.

0(x₁,…,x_n)=0 )=0(x_i)=0;

k(x₁,…,x_n)= =k

2. Оператор примитивной рекурсии

В основе этого оператора лежит хорошо известный способ вычисления функции натурального аргумента – метод рекурсии: задается f(0) и так называемая рекуррентная формула f(n+1)=h(f(n)). С помощью этой формулы последовательно вычисляется f(1), f(2) и т.д.

Пусть g(x₁,…,x_n) – n-местная функция, h(x₁,…,x_n,y,z) – (n+2)-местная функция. Тогда результатом применения оператора примитивной рекурсии к функциям g и h называется (n+1)-местная функция z=f(x₁,…,x_n,y), построенная по следующему правилу:

f(x₁,…,x_n,0)=g(x₁,…,x_n);

f(x₁,…,x_n,y+1)=h(x₁,…,x_n,y,f(x₁,…,x_n,y)).

Обозначается f=R(g,h).

Оператор примитивной рекурсии можно применять по любым переменным, входящим в функции f, g, h, но всегда нужно указывать, по какой переменной этот оператор проводится.

Пример. Найдите функции g и h в рекурсивной формуле для двуместной функции z=f(x,y)=xy, если рекурсия проводится по переменной х.

Решение.

g(y)=f(0,y)=0y=0 – начальное условие;

h(x,y,f(x,y))=f(x+1,y)=(x+1)y=xy+y=f(x,y)+y=z+y – рекуррентная формула.

Арифметическая функция называется примитивно рекурсивной (ПРФ), если она получена из базисных функций при помощи конечного числа применений оператора суперпозиции и оператора примитивной рекурсии. Базисные функции являются примитивно рекурсивными по определению. Всякая примитивно рекурсивная функция является вычислимой, так как процесс ее определения дает способ вычисления значений функции для любых значений ее аргументов.

Пример. Докажите, что функция f(x,y) принадлежит классу ПРФ.

1. z=x+y (s(x,y))

2. z=xy (p(x,y))

3. z=x^y (q(x,y))

Решение.

1. Проведем рекурсию по переменной х.

g(y)=f(0,y)=0+y=y= – ПРФ

h(x,y,f(x,y))=f(x+1,y)=x+1+y=x+y+1=f(x,y)+1=z+1= - ПРФ

z=R(g,h) - ПРФ

2. z=R(g,h)=R(0,z+y)=R 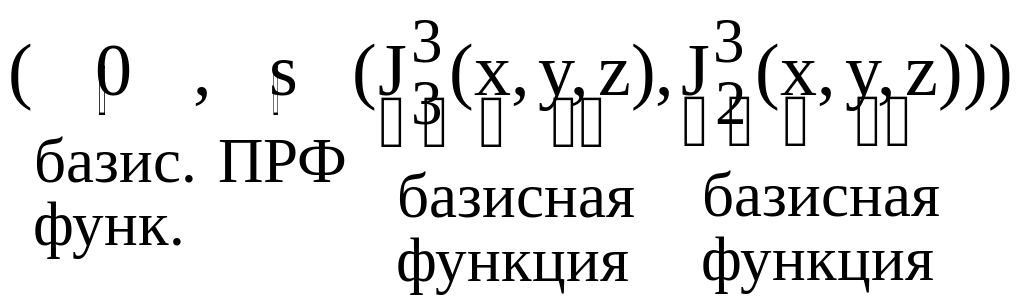- ПРФ

3. Проведем рекурсию по переменной y.

g(x)=f(x,0)=x⁰=1= – ПРФ

h(x,y,f(x,y))=f(x,y+1)=x^y+1=x^yx=f(x,y)x=zx= – ПРФ

z=R(g,h) - ПРФ

Однако существуют вычислимые функции, которые не являются примитивно рекурсивными.

Так как базисные функции определены везде (ℕ{0}), то и примитивно рекурсивные функции определены везде. Однако функция вычитания z=x-y на множестве ℕ{0} определена только при x≥y, т.е. не является примитивно рекурсивной функцией.

3. Оператор минимизации

Пусть f – не всюду определенная n-местная функция. Результатом применения оператора минимизации к функции f называется (n-1)-местная функция h, построенная по следующему правилу:

h(x₁,…,x_n-1)=y при условии, что f(x₁,…,x_n-1,y)=0 и f(x₁,…,x_n-1,t) определена для любых t<y и отлична от нуля.

Обозначается h(x₁,…,x_n-1)= .

Пример. x-y – это наименьшее z, которое при сложении с y даст x.

h(x,y)=x-y, f(x,y,z)=x-y-z, x-y=_z(x-y-z=0).

Арифметическая функция называется частично рекурсивной (ЧРФ), если она получена из базисных функций при помощи конечного числа применений операторов суперпозиции, примитивной рекурсии и минимизации.

Из определения вытекают следующие свойства частично рекурсивных функций:

1. Каждая ПРФ является ЧРФ;

2. Класс ЧРФ шире класса ПРФ, так как среди них встречаются не всюду определенные функции, откуда и пошло их название.

Проводя аналогии с программными функциями, можно заметить, что ПРФ соответствуют программным функциям, использующим арифметические циклы, условные операторы, арифметические операции; ЧРФ – программным функциям, использующим цикл while.

Какие бы классы алгоритмов до сих пор не строились, во всех случаях оказывалось, что числовые функции, вычисляемые посредством этих алгоритмов, были частично рекурсивными. Поэтому общепринятым считается следующий тезис.

Тезис Черча. Класс частично рекурсивных функций совпадает с классом вычислимых функций.