2.3 Корпускулярно-волновой дуализм

1. В чем заключается корпускулярно- волновой дуализм света?

Дуазим света заключается в том, что свет проявляет в одних случаях волновые свойства (интерференция, дифракция, дисперсия, поляризация), а в других – корпускулярные (фотоэффект, тепловое излучение, эффект Комптона).

2. Опыт Дэвиссона и Джермера.

Опыт Дэвиссона и Джермера – опыт, основанный на угловом распределениеи электронов, рассеивающихся на монокристалле никеля, в результате которого была экспериментально доказана гипотеза де Бройля.

3. В чем суть гипотезы де Бройля?

Суть гипотезы де Бройля состоит в том, что волновые свойства присущи абсолютно всем материальным объектам. 

4. Выражение для длины волны де Бройля.

.

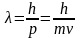5. Каким экспериментом была подтверждена гипотеза де Бройля?

Гипотеза де Бройля была подтверждена опытом Дэвиссона и Джермера, а также экспериментом Томсона.

6. Почему макротела не проявляют волновые свойства?

Считается, что макротела проявляют только корпускулярные свойства и не проявляет волновые свойства, т.к. их длина волны де Бройля лежит за пределами доступной наблюдению области.

14. В чем суть соотношений неопределенностей Гейзенберга?

Суть состоит в том, что микрообъекты не могут иметь одновременно точных значений координаты и импульса.

14. Запишите соотношение неопределенностей для координаты и импульса.

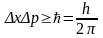
14. Запишите соотношение неопределенностей для энергии и времени.

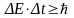
24. Какой имеют смысл 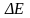и 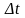в соотношении ?

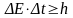Здесь представляет собой время, в течение которого микрочастица обладает энергией

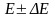
24. Сформулируйте принцип дополнительности Бора.

Для того, чтобы наиболее адекватно описать физический объект, относящийся к микромиру, его нужно описывать во взаимоисключающих, дополнительных системах, например одновременно и как частицу, и как волну.

24. Как называется раздел современной теоретической физики, изучающий законы движения частиц в области микромира?

Квантовая механика

2.4 Временное и стационарное уравнения Шредингера

1. Запишите временное уравнение Шредингера.

2. Запишите стационарное уравнение Шредингера.

3. Что называют собственным значением энергии? Собственной волновой функцией?

4. В чем отличие стационарного и временного уравнений Шредингера?

5. Граничные условия для частицы в потенциальной яме с бесконечно высокими стенками.

6. Собственная волновая функция частицы в одномерном потенциальном ящике имеет вид 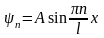. Как можно определить коэффициент пропорциональности А в этом выражении?

7. Собственные значения энергии частицы в одномерном потенциальном ящике имеют вид 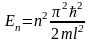. Каково расстояние между 3-м и 4-м энергетическими уровнями?

8. Собственные значения энергии частицы в одномерном потенциальном ящике имеют вид . Каково расстояние между 1-м и 2-м энергетическими уровнями?

9. Собственные значения энергии частицы в одномерном потенциальном ящике имеют вид . Во сколько раз отличаются значения энергии электрона и протона, находящихся в одинаковых ящиках?

10. Собственные значения энергии частицы в одномерном потенциальном ящике имеют вид . Как изменится энергия электрона в основном состоянии, если ширину ящика уменьшить в 2 раза.

11. Квантовая частица в бесконечно глубокой прямоугольной одномерной потенциальной яме имеет дискретный энергетический спектр (энергия частицы квантована). Как зависит эта энергия от значения квантового числа n?

12. Чему равна величина Dy в уравнении Шредингера ?

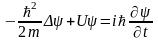13. Что называют туннельным эффектом?

14. На рисунке показана зависимость квадрата модуля волновой функции, определяющей состояние электрона в одномерной «потенциальной яме» шириной L в квантовом состоянии при n = 1. Какая из указанных координат соответствует состоянию, в котором вероятность обнаружить электрон наибольшая?

15. Энергия электрона в одномерной «потенциальной яме» шириной l определяется формуло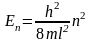й . Как изменяется относительный энергетический интервал между уровнями 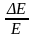при возрастании квантового числа n?